ММ-8. АЛГЕБРАИЧЕСКАЯ ПРОБЛЕМА СОБСТИЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ КВАДРАТНОЙ МАТРИЦЫ
Ключевые слова и понятия
8.1. Собственно значение матрицы.
8.2. Собственный вектор матрицы.
8.3. Метод обратных итераций.
8.4. Степенной метод.
8.5. Метод сдвига.
8.1. Входная информация для самопроверки.
Для изучения данной темы Вам необходимо восстановить в памяти:
- из курса прикладной математики – решение систем линейных однородных и неоднородных алгебраических уравнений,понятия линейной и векторной алгебры, собственные значения и собственные вектора квадратной матрицы, системы линейно независимых векторов;
- из настоящего спецкурса - понятия: линейного пространства, подпространства и нормированного пространства.
8.2. Содержание темы.
8 .2.1. Структурно – логическая схема содержания темы
Квадратная матрица
8 .2.2. Тематическое содержание.
Напомним некоторые сведения из курса линейной алгебры.
Если А
— квадратная
матрица п-го
порядка и
при
,
то число
называется собственным,
значением
матрицы, а
ненулевой вектор х
— соответствующим
ему собственным
вектором. Перепишем
задачу в виде
(8.1.)
Для существования нетривиального решения задачи (8.1) должно выполняться условие
(8.2)
Этот определитель
является многочленом
-й
степени относительно
;
его называют
характеристическим
многочленом. Значит,
существует п
собственных
значений — корней этого многочлена,
среди которых
могут быть одинаковые (кратные). В
принципе можно вычислить
характеристический многочлен и найти
все его корни.
Если найдено некоторое собственное значение, то, подставляя его в однородную систему (8.1), можно определить соответствующий собственный вектор. Будем нормировать собственные векторы. Тогда каждому простому (не кратному) собственному значению соответствует один (с точностью до направления) собственный вектор, а совокупность всех собственных векторов, соответствующих совокупности простых собственных значений, линейно – независима. Таким образом, если все собственные значения матрицы простые, то она имеет п линейно-независимых собственных векторов, которые образуют базис пространства .
Пример.
Заданы
осевые и центробежные моменты инерции
некоторого пространственного тела в
центральных осях:
=6
кн
,
=5
кн
,
=7
кн
,
=-2
кн
,
=2
кн
,
=0.
Найти значения главных центральных
моментов инерции и их направления.
Решение.
Составим матрицу центральных моментов инерции
A=
=
.
Запишем характеристическое уравнение (8.2) и найдем собственные значения этой матрицы:
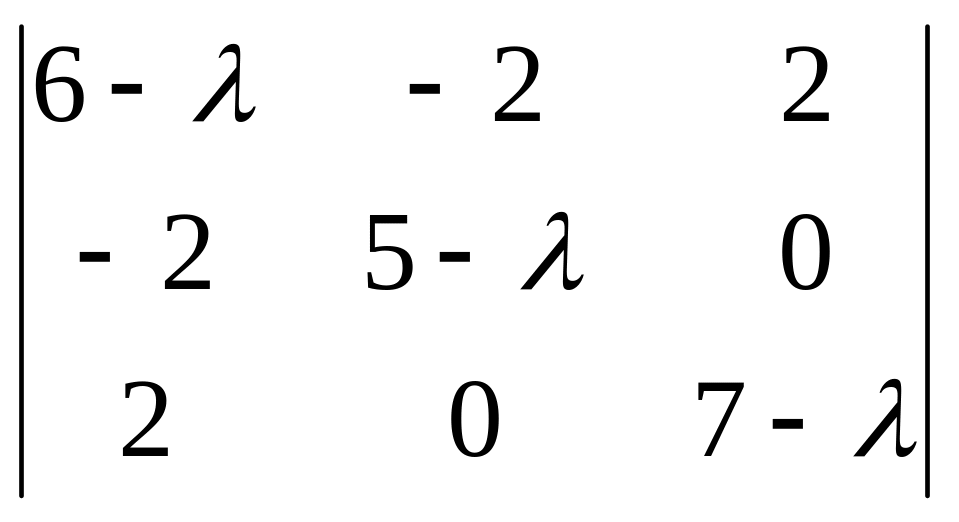=0.
Раскрывая определитель , получим:
(6-
)(5-
)(7-
)
– 4(5-
)-4(7-
)=0,
(
.
Отсюда
находим собственные значения матрицы:
=3,
=6,
=9.
Найдем
собственный вектор
,
соответствующий первому собственному
значению
=3
из уравнения (8.1)
(A-3E)
=0.
Запишем это уравнение в координатной форме
Преобразуем данную систему линейных алгебраических уравнений по методу Гаусса:
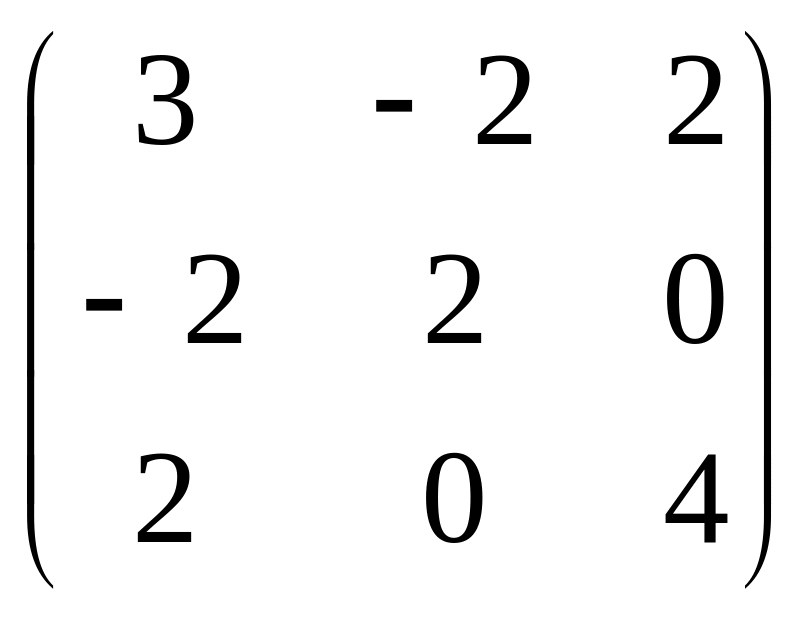
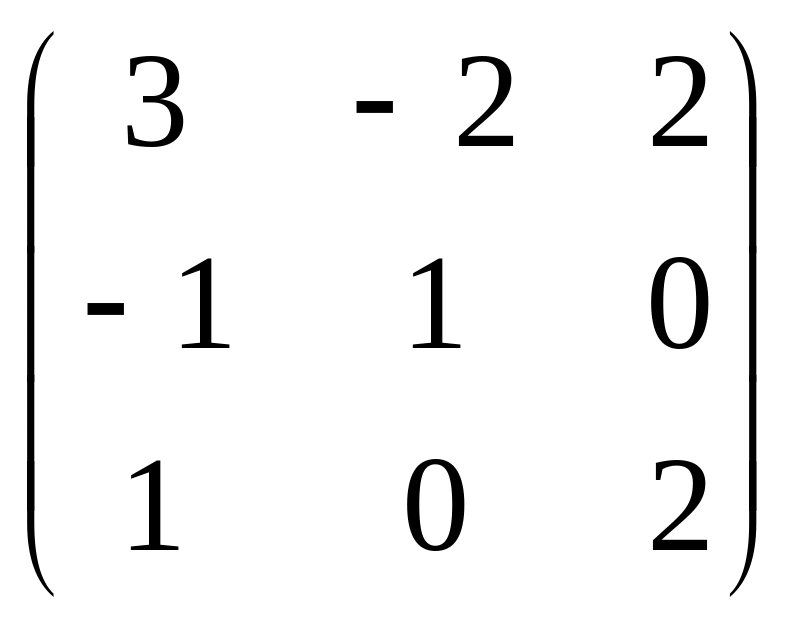
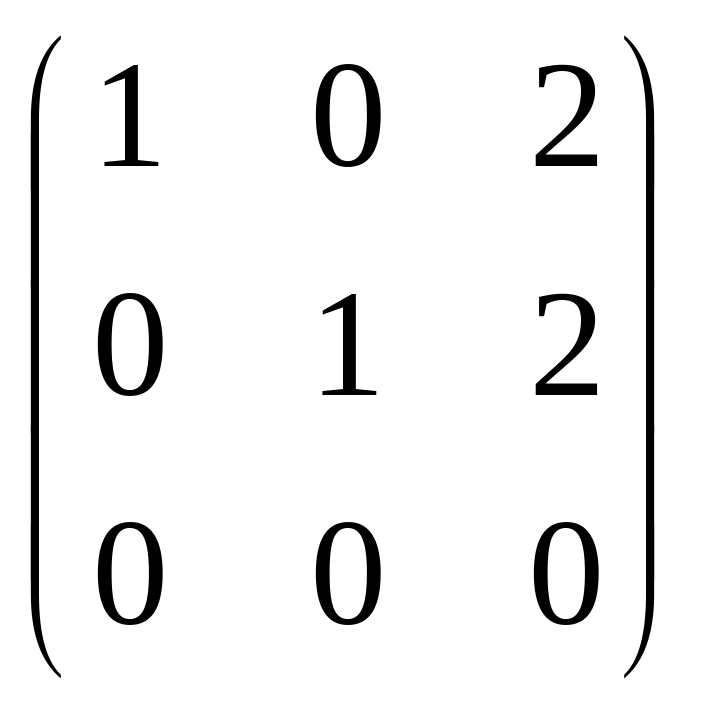
Таким
образом, система имеет решение:
,
,
а собственный вектор
.
Найдем
собственный вектор
,
соответствующий второму собственному
значению
=6
из уравнения (8.1)
(A-6E)
=0.
Запишем это уравнение в координатной форме
Преобразуем данную систему линейных алгебраических уравнений по методу Гаусса:
.
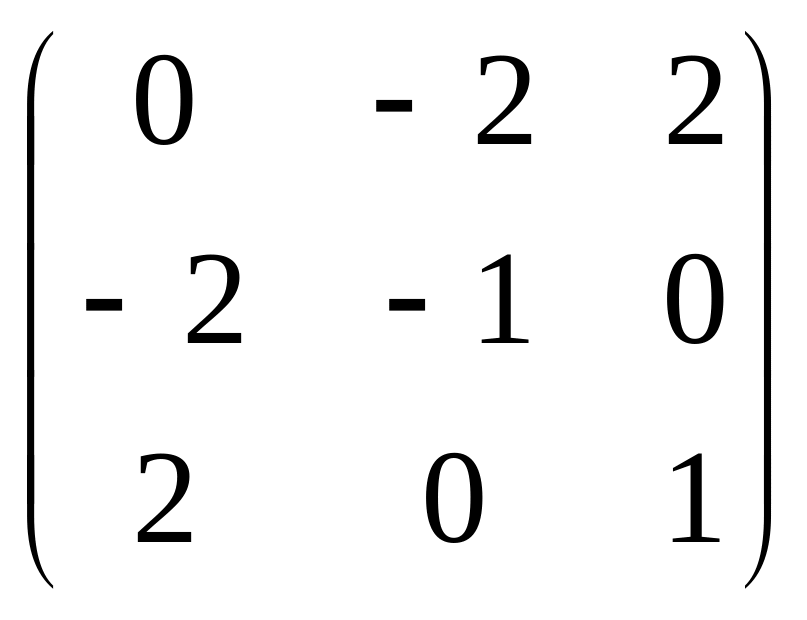
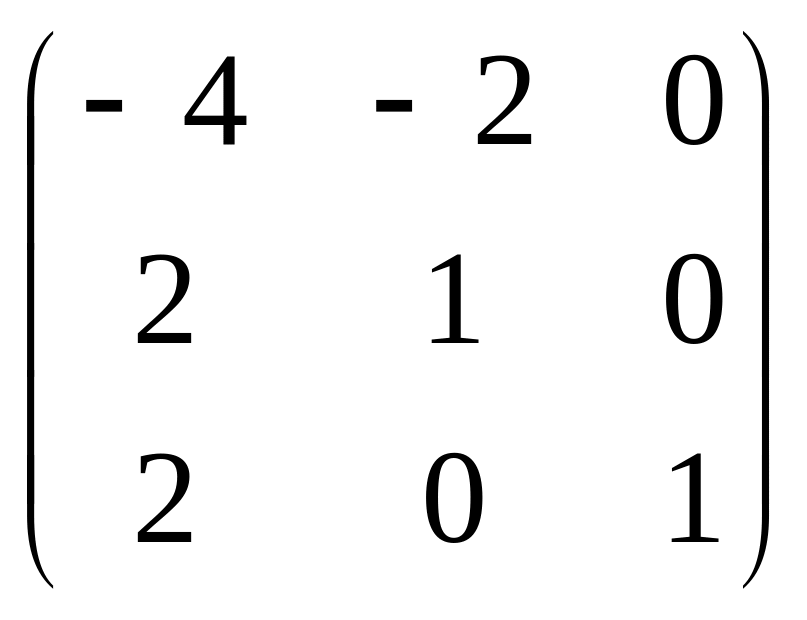
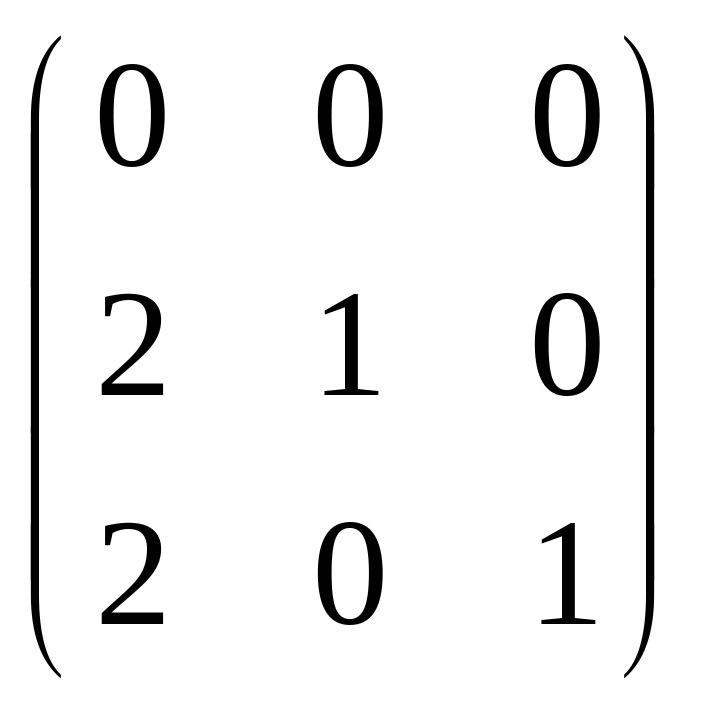Таким
образом, система имеет решение:
,
,
а собственный вектор
.
Найдем
собственный вектор
,
соответствующий второму собственному
значению
=9
из уравнения (8.1)
(A-9E)
=0.
Запишем это уравнение в координатной форме
Преобразуем данную систему линейных алгебраических уравнений по методу Гаусса:
.
.
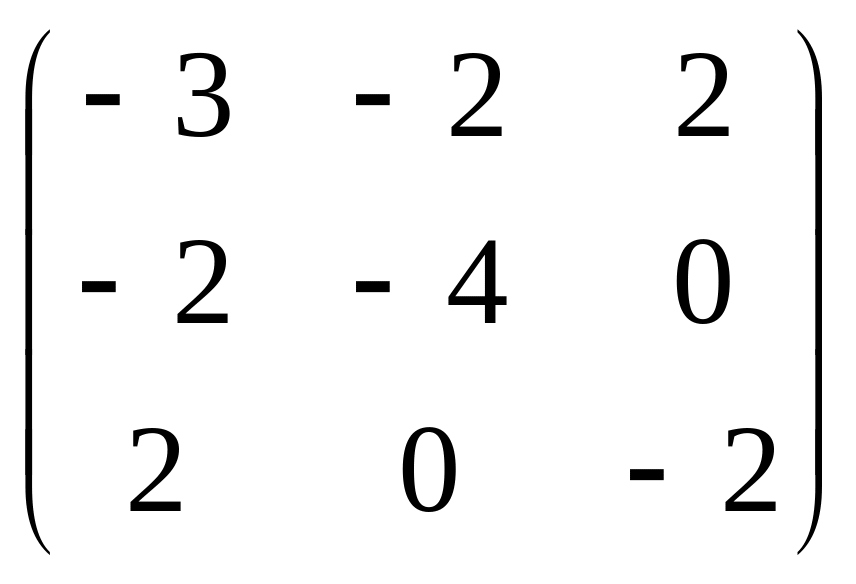
Таким
образом, система имеет решение:
,
,
а собственный вектор
.
Однако, если степень многочлена достаточно высокая, то аналитически определить корни достаточно сложно. И в этом случае их определяют численными методами.
Если
собственное значение известно, то
собственный вектор .удовлетворяет
системе (8.1).
Но любой численный метод дает вместо
точного собственного значения
приближенное значение
,
так что
,
хотя отличается от нуля очень мало. В
таком случае задача
при использовании приближенного
собственного значения имеет только
тривиальное решение
x=0.
Поэтому при численных расчетах находить
собственные векторы непосредственно
из системы (8.1)
нельзя.