3 ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

Для изучения вращательного движения твердого тела вокруг неподвижной оси воспользуемся теоремой об изменении момента количества движения (кинетического момента) механической системы относительно оси (3.10):

dK_z/dt = M_z^e.    (3.11)

Пусть на твердое тело, имеющее неподвижную ось вращения z(рисунок 3.4), действует система заданных внешних активных сил (F₁, F₂, F₃,…, F_n), определяющих угловую скорость ω и угловое ускорение ε этого тела в его вращательном движении вокруг оси z. Одновременно на это же тело действуют силы реакции R_A подпятника и R_B радиального подшипника.

Определяем правую часть уравнения (3.11):

M_z^e=∑M_z(F_j^e)+M_z(R_A)+M_z(R_B).

Поскольку

M_z(R_A) = M_z(R_B)=0,

то

M_вращ = M_z^e= ∑M_z(F_j^e).

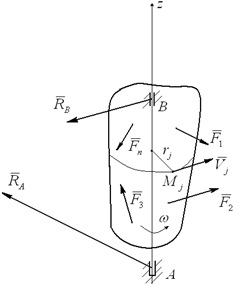
Рисунок 3.4

Найдем момент количества движения (кинетический момент) K_zвращающегося твердого тела. Для этого выделим точку M_j тела на расстоянии r_j от оси вращения и имеющую скорость V_j=ω∙r_j. Очевидно, что

K_zj=m_j ∙V_j ∙ r_j=m_j ∙ ω ∙ r_j²

Тогда момент количества движения (кинетический момент) всего вращающегося тела будет:

K_z = ∑K_zj = ∑m_j ∙ ω ∙ r_j²,

где ∑m_j ∙ r_j²= J_z.

Следовательно, окончательно будем иметь

K_z = J_z ∙ ω.    (3.12)

Подставляя в уравнение (3.11) выражение (3.12), получаем

J_z ∙ dω/dt = M_вращ,

или

J_z ∙ d²φ/dt² = M_вращ.    (3.13)

Уравнение (3.13) представляет собой дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси.

Поскольку dω/dt = ε, имеем

ε = M_вращ/J_z.    (3.14)

Полученное выражение (3.14) показывает, что осевой момент инерции J_z тела следует рассматривать как меру инертности твердого тела при его вращательном движении вокруг неподвижной оси.

Изменение момента количества движения механической системы

Рассмотрим механическую систему, состоящую из nматериальных точек. Выделим из этой системы некоторую точку M_j с массой m_j (рисунок 3.3). На выделенную точку в итоге будут действовать две силы: равнодействующая внешних сил и равнодействующая внутренних сил (F_j^e и F_jⁱ соответственно).

Для выделенной точки M_j, как для свободной точки, можем применить теорему об изменении момента количества движения (кинетического момента) (3.4):

dK_0j/dt = M₀(F_j^e) + M₀(F_jⁱ).    (3.6)

Рисунок 3.3

Аналогичные уравнения запишем для всех точек системы (j=1,2,3,…,n) и сложим их почленно:

∑dK_0j / dt = ∑M₀(F_j^e) + ∑M₀(F_jⁱ).    (3.7)

Рассмотрим каждую сумму в отдельности:

∑dK_0j / dt = d∑K_0j / dt = dK₀ / dt,    (3.8)

где ∑K_0j = K₀ – главный момент количества движения (кинетический момент) механической системы относительно некоторого центра O; ∑M₀(F_j^e) = M₀^e – главный момент внешних сил механической системы; M₀(F_jⁱ) = M₀^j = 0 – главный момент внутренних сил механической системы, который равен нулю (по свойству внутренних сил механической системы).

В итоге получаем

dK₀ / dt = M₀^e.    (3.9)

Уравнение (3.9) выражает теорему об изменении главного момента количества движения (кинетического момента) механической системы: производная по времени от главного момента количества движения (кинетического момента) механической системы относительно некоторого неподвижного центра равна главному моменту всех внешних сил, действующих на эту систему, относительно того же центра.

Проецируя равенство (3.9) на неподвижные оси декартовой системы координат, получаем

dK_x/dt = M_x^e; dK_y/dt = M_y^e; dK_z/dt = M_z^e.    (3.10)

Уравнения (3.10) выражают собой теорему об изменении кинетического момента системы относительно координатных осей: производная по времени от момента количества движения (кинетического момента) механической системы относительно какой-либо неподвижной оси равна главному моменту всех внешних сил, действующих на эту систему, относительно той же оси.

Рассмотрим следствия из теорем (3.9) и (3.10).

Следствие 1

Если главный момент внешних сил системы относительно центра равен нулю (M₀^e), то, согласно (3.9), момент количества движения (кинетический момент) системы относительно того же центра остается постоянным по величине и направлению, т.е. M₀ = const.

Этот частный случай выражает закон сохранения момента количеств движения (кинетического момента) системы относительно центра.

Следствие 2

Если сумма моментов всех внешних сил системы относительно какой-либо оси равна нулю, например, M_x^e = ∑M_x(F_j^e) = 0, то из (3.10) следует, что K_x = const, т.е. момент количества движения (кинетический момент) механической системы относительно этой оси остается постоянным.

Из теорем об изменении момента количества движения (кинетического момента) механической системы относительно центра (3.9) и относительно оси (3.10), а также следствий из них следует, что внутренние силы не могут непосредственно изменить момент количеств движения (кинетический момент) изолированной механической системы.

Внутренние силы могут влиять на момент количества движения (кинетический момент) механической системы в том случае, если их действие приводит к возникновению внешних сил, т.е. косвенным образом через возникновение внешних сил.

Приведенные выше теоремы об изменении момента количества движения (кинетического момента) механической системы (3.9) и (3.10) остаются справедливыми и по отношению к подвижным осям координат, имеющим свое начало в центре системы и движущимся поступательно вместе с центром масспо отношению к неподвижным осям координат.

ИЗМЕНЕНИЕ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ

Рассмотрим материальную точку M массой m, движущуюся под действием силы F (рисунок 3.1). Запишем и построим вектор момента количества движения (кинетического момента) M₀материальной точки относительно центра O:

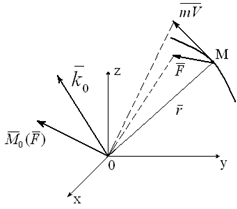
Рисунок 3.1

Дифференцируем выражение момента количества движения (кинетического момента k₀) по времени:

Так как dr/dt=V, то векторное произведение V × m∙V(коллинеарных векторов V и m∙V) равно нулю. В то же время d(m∙V)/dt=F согласно теореме о количестве движения материальной точки. Поэтому получаем, что

dk₀/dt = r×F,    (3.3)

где r×F = M₀ (F) – вектор-момент силы F относительно неподвижного центра O. Вектор k₀ ⊥ плоскости (r, m×V), а вектор M₀(F) ⊥ плоскости (r, F), окончательно имеем

dk₀/dt = M₀(F).    (3.4)

Уравнение (3.4) выражает теорему об изменении момента количества движения (кинетического момента) материальной точки относительно центра: производная по времени от момента количества движения (кинетического момента) материальной точки относительно какого-либо неподвижного центра равна моменту действующей на точку силы относительно того же центра.

Проецируя равенство (3.4) на оси декартовых координат, получаем

dk_x/dt = M_x(F);

dk_y/dt = M_y(F);

dk_z/dt = M_z(F).    (3.5)

Равенства (3.5) выражают теорему об изменении момента количества движения (кинетического момента) материальной точки относительно оси: производная по времени от момента количества движения (кинетического момента) материальной точки относительно какой-либо неподвижной оси равна моменту действующей на эту точку силы относительно той же оси.

Рассмотрим следствия, вытекающие из теорем (3.4) и (3.5).

Следствие 1

Рассмотрим случай, когда сила F во все время движения точки проходит через неподвижный центр O (случай центральной силы), т.е. когда M₀(F) = 0. Тогда из теоремы (3.4) следует, что k₀ = const, т.е. в случае центральной силы момент количества движения (кинетический момент) материальной точки относительно центра этой силы остается постоянным по модулю и направлению (рисунок 3.2).

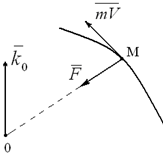
Рисунок 3.2

Из условия k₀ = const следует, что траектория движущейся точки представляет собой плоскую кривую, плоскость которой проходит через центр этой силы.

Следствие 2

Пусть M_z(F) = 0, т.е. сила пересекает ось z или параллельна ей.

В этом случае, как это видно из третьего из уравнений (3.5), k_z = const, т.е. если момент действующей на точку силы относительно какой-либо неподвижной оси всегда равен нулю, то момент количества движения (кинетический момент) точки относительно этой оси остается постоянным.

9 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ

Рассмотрим движение произвольной точки системы из первого положения во второе:

где F_k^e — внешние силы, действующие на систему, F_kⁱ — внутренние силы системы.

Умножим обе части уравнения скалярно на дифференциал радиуса-вектора dr_k тогда

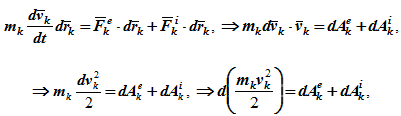
или dT_k = dA_k^e + dA_kⁱ , (1.1)

где T_k — кинетическая энергия точки;

далее получим

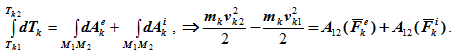
Просуммируем по всем точкам системы

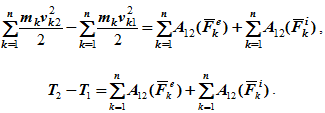
То есть, изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на систему, на том же перемещении.

Если в формуле (1.1) обе части уравнения разделить на dt, то можно записать теорему об изменении кинетической энергии системы в дифференциальной форме: производная по времени от кинетической энергии механической системы равна сумме мощностей внешних и внутренних сил, действующих на систему.

dT_k / dt = dA_k^e / dt + dA_kⁱ / dt dT_k / dt = N_k^e + N_kⁱ.

Суммируя по всем точкам системы, получим

dT / dt = ∑N_k^e + ∑N_kⁱ.

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ

Кинетической энергией механической системы называется сумма кинетических энергий всех точек этой системы:

T = ∑m_kv_k²/2,

где m_k и v_k — масса и скорость k-й материальной точки, принадлежащей данной системе.

На основании теоремы Кёнига кинетическая энергия произвольной механической системы определяется по формуле

T = Mv_C²/2 + ∑ m_kv_kr²/2

где M — масса всей системы; v_C — скорость центра масс системы; m_k — масса k-й точки системы; v_kr — относительная скорость k-й точки при движении её вокруг центра масс (т.е. v_k=v_C +v_kr).

Из этой формулы можно получить следующие частные случаи для твёрдого тела:

1. при поступательном движении тела

v_k= v_C , v_kr=0,

T = mv_C²/2;

2. при вращении тела вокруг оси, проходящей через его центр масс,

v_C=0 , v_kr= ω × r_k ,

T = ∑ m_kv_kr²/2 = Jω²/2,

где J — момент инерции тела относительно оси, проходящей в данный момент времени через центр масс; ω — угловая скорость вращения тела;

3. в случае произвольного движения тела (например при плоскопараллельном движении)

T = mv_C²/2 + Jω²/2.

11 СВЯЗИ В МЕХАНИКЕ

Связями называются любого вида ограничения, накладываемые на положения, скорости точек механической системы, независящие от действующих сил.

Связи неизменяемые со временем называются стационарными, изменяемые – нестационарными.

Связи бывают удерживающие, когда ограничения сохраняются при любом положении системы и неудерживающие, которые этим свойством не обладают.

Связи, налагающие ограничения на координаты точек системы называются геометрическими, а накладывающие ограничения на скорости точек системы кинематическими или дифференциальными.

Если дифференциальную связь можно представить как геометрическую (проинтегрировать), то такая связь называется интегрируемой, в противном случае не интегрируемой.

Геометрические интегрируемые дифференциальные связи называются голономными, а неинтегрируемые дифференциальные связи неголономными. Соответственно и системы разделяют на голономные (с голономными связями) и неголономные (с неголономными связями).

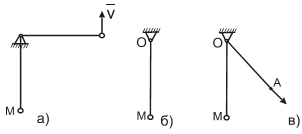
Рис. 1.1

Пример. На рис. 1.1а, шарик М в плоскости закреплен через стержень с шарниром О – стационарная удерживающая голономная связь V=ω ∙ l, интегрируем S=φ ∙ l.

Рис. 1.1б, – ОМ – нить, – в этом случае это неудерживающая, стационарная связь.

Рис. 1.1в, – нить продернута в кольцо О, конец А нити движется со скоростью u — неудерживающая нестационарная связь, ее уравнение:

x²+ y²— (l₀+ u ∙ t)²≤ 0

Эффект механических связей можно учитывать и рассматривая перемещения, которые допускаются наложенными связями. Возможными перемещениями механической системы называется любая совокупность элементарных (бесконечно малых) перемещений точек системы из занимаемого в данный момент времени положения, которое допускается наложенными на систему связями. Связи называются идеальными, если сумма элементарных работ их реакций на любом возможном перемещении равна нулю.

Например: тело на гладкой поверхности, реакция опорынаправлена по нормали к поверхности, δS — возможное перемещение (рис. 1.2).

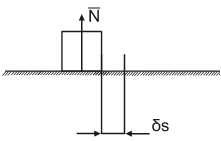
Рис. 1.2

Элементарная работа реакции связи:

δA=N × δS=N ∙ δS ∙ cos90⁰= 0

т.е. связь идеальна.