Экзамен / тмм - экзамен(и задачи) / ТММ / tmm_8

3.7. Свойства эвольвенты окружности и эвольвентного зацепления

В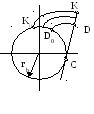 качестве главного профиля зубьев цилиндрических зубчатых колес, применяемых в машиностроении, наибольшее распространение получил эвольвентный профиль. Плоская эвольвента окружности представляет собой траекторию любой точки прямой линии, перекатываемой без скольжения по эволюте, т.е. по основной окружности радиуса r_b (рис.3.42). Перекатываемая по основной окружности прямая называется производящей прямой. Рассмотрим более подробно свойства эвольвенты окружности.

1. Нормаль к эвольвентам (прямая КС) касается основной окружности, причем точка касания (С) является центром кривизны эвольвент.

2. Все эвольвенты одной основной окружности эквидистантны, и расстояние KD между ними равно длине дуги К₀D₀.

3. Каждая ветвь эвольвенты вполне определяется радиусом основной окружности и положением начала отсчета эвольвентного угла.

4. Эвольвента не имеет точек внутри основной окружности.

Из свойств эвольвенты вытекают свойства эвольвентного зацепления. Пусть профиль зуба колеса 1 (рис.3.43) очерчен по эвольвенте основной окружности с радиусом r_b1, а профиль зуба колеса 2 – по эвольвенте основной окружности радиуса r_b2. Поместим центры этих окружностей в центры вращения 0₁ и 0₂. Нормаль к эвольвенте первого колеса должна быть касательной к основной окружности первого колеса, а нормаль к эвольвенте второго колеса должна быть касательной к основной окружности второго колеса. В точке касания эвольвент нормаль должна быть общей к обоим профилям, и, следовательно, точка контакта лежит на общей касательной к основным окружностям. При вращении ведущего колеса 1 против часовой стрелки, а ведомого колеса 2 – по часовой (рис.3.43, а) точка касания эвольвент перемещается по отрезку В₁В₂ этой касательной, т.к. вне отрезка В₁В₂ эвольвенты не могут касаться, т.е. иметь общую нормаль; В₁В₂ является линией зацепления.

Точка пересечения общей нормали к эвольвентам с линией межосевого расстояния 0₁0₂ является полюсом зацепления Р и занимает неизменное положение.

Если направление вращение ведущего колеса 1 и ведомого колеса 2 изменится, то линия зацепления В₁В₂, по которой перемещается точка контакта, займет новой положение (рис.3.43, б).

Угол между линией зацепления В₁В₂ и прямой, перпендикулярной линии межосевого расстояния, называется углом зацепления и обозначается через _w. Углы РВ₁0₁ и РВ₂0₂ равны углу зацепления _w как углы с соответственно перпендикулярными сторонами. Поскольку Р0₁ = r_w1, а Р0₂ = r_w2, то

. (3.87)

Следовательно, при эвольвентном зацеплении передаточное отношение может быть выражено через отношение радиусов основных окружностей:

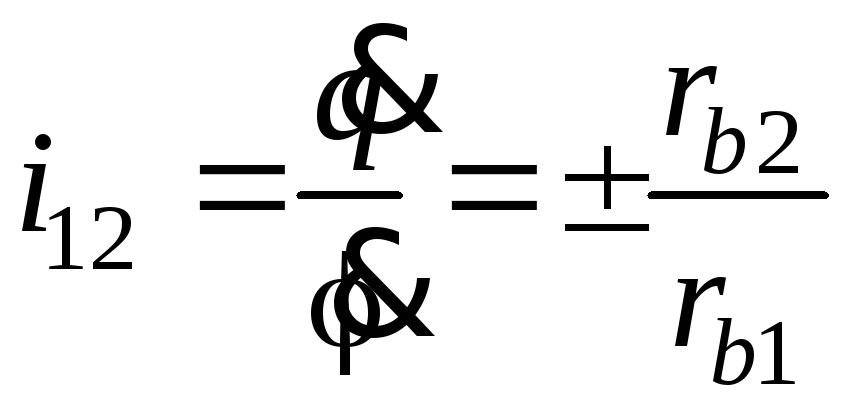, (3.88)

причем знак плюс относится к внутреннему зацеплению, а знак минус – к внешнему.

Из формулы (3.88) видно, что при эвольвентном зацеплении изменение межосевого расстояния не влияет на значение передаточного отношения вследствие неизменности радиусов основных окружностей. При изменении межосевого расстояния изменяются лишь радиусы начальных окружностей и угол зацепления.

С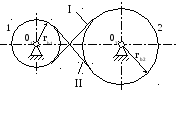войства эвольвентного зацепления иллюстрирует аналогия с перекрестно-ременной передачей (рис.3.44). Линия зацепления как бы сматывается с ведущего шкива 1 радиуса r_b1 и наматывается на шкив 2 радиуса r_b2 (ветвь I при вращении ведущего шкива 1 против часовой стрелки и ветвь II при вращении шкива 1 по часовой стрелке). При изменении межосевого расстояния 0₁0₂ передаточное отношение, обратно пропорциональное отношению радиусов шкивов r_b2 и r_b1, не изменяется.

3.8. Теоретический и производящий исходные контуры

Геометрия зубчатого колеса зависит в первую очередь от размеров и формы инструмента. Поэтому стандартизация параметров инструмента, воспроизводящего эвольвентный профиль зубчатого колеса, необходима с технической и экономической точек зрения. За основу стандарта форм и размеров зубчатого колеса принят теоретический исходный контур (ТИК, рис.3.45), который представляет собой чередующиеся симметричные зубья и впадины трапециевидной формы. Размеры теоретического исходного контура установлены государственным стандартом. Базовая линия теоретического исходного контура, по которой толщина зуба равна ширине впадины, называется его делительной прямой. Расстояние между одноименными профилями соседних зубьев по делительной или по любой другой параллельной ей прямой называют шагом зубьев р исходного контура.

Если форма инструмента повторяет форму ТИК, а делительная прямая является начальной прямой, то начальная окружность нарезаемого колеса касается делительной прямой ТИК. Как уже отмечалось ранее, подвижные центроиды катятся друг по другу без скольжения, поэтому шаг зубьев по начальной окружности колеса должен быть равен шагу зубьев ТИК. Если z – число зубьев нарезаемого колеса, то длина окружности – подвижной центроиды колеса – равна:

, (3.89)

где d – диаметр подвижной центроиды колеса:

. (3.90)

Подвижную центроиду колеса при его зацеплении с рейкой называют делительной окружностью. Делительная окружность делит зуб на делительную головку и делительную ножку. В выражении (3.90) введен основной параметр зубчатого зацепления – модуль m:

. (3.91)

Модуль измеряется в миллиметрах и может принимать только значения, оговоренные государственным стандартом. В долях модуля задаются все линейные размеры контура:

высота делительной головки

, (3.92)

высота делительной ножки

, (3.93)

радиус переходной кривой

, (3.94)

где - коэффициент высоты головки; с^* - коэффициент радиального зазора; - коэффициент радиуса переходной кривой.

Угол  между главным профилем зуба (прямая линия бокового профиля зуба является вырожденной эвольвентой окружности при r_b  ) и осью симметрии зуба называется углом профиля исходного контура. Государственный стандарт устанавливает следующие значения параметров исходного контура:

с* = 0,25; = 0,384;  = 20⁰.

Исходным производящим контуром называется такой, который заполняет впадины теоретического исходного контура, как отливка заполняет форму (см. рис.3.45, ИПК). При этом между прямой вершин теоретического исходного контура и прямой впадин исходного производящего контура сохраняется радиальный зазор с^*m. Это делается для того, чтобы поверхность впадин инструмента, образованного на базе исходного производящего контура, не участвовала в процессе нарезания зубьев.

Если рассмотренный исходный производящий контур двигать вдоль линий зубьев, перпендикулярных его плоскости, им будут описаны поверхности исходной производящей зубчатой рейки (ее иногда называют инструментальной), прямозубой или косозубой, в зависимости от равного или не равного нулю угла наклона линий ее зубьев. В соответствии с этим такой контур можно было бы определить как сечение рейки плоскостью, перпендикулярной линиям ее зубьев (нормальный контур).

3.9. Геометро-кинематические условия существования эвольвентного зацепления

1. Основная теорема зацепления применительно к эвольвентному зацеплению записывается так:

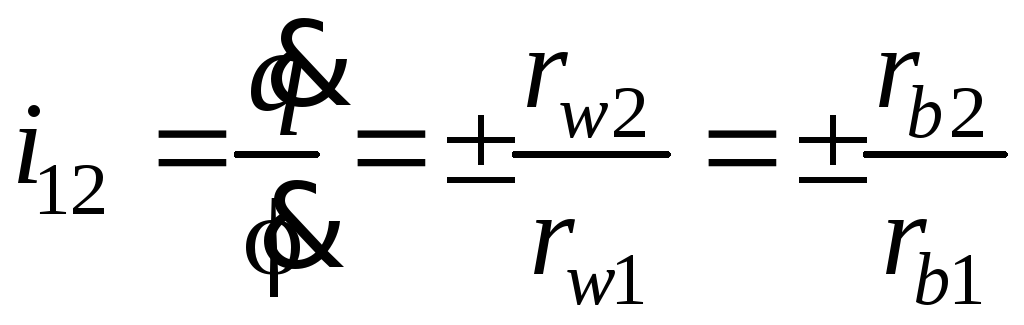. (3.95)

где r_w1, r_w2, r_b1, r_b2 – радиусы начальных и основных окружностей.

2. Полный коэффициент перекрытия _ является суммой торцового коэффициента перекрытия _ и осевого коэффициента перекрытия _, т.е.

_ = _ + _ . (3.96)

Значение торцового коэффициента перекрытия может быть вычислено как отношение длины активной линии зацепления g_ к шагу эвольвентного зацепления р_:

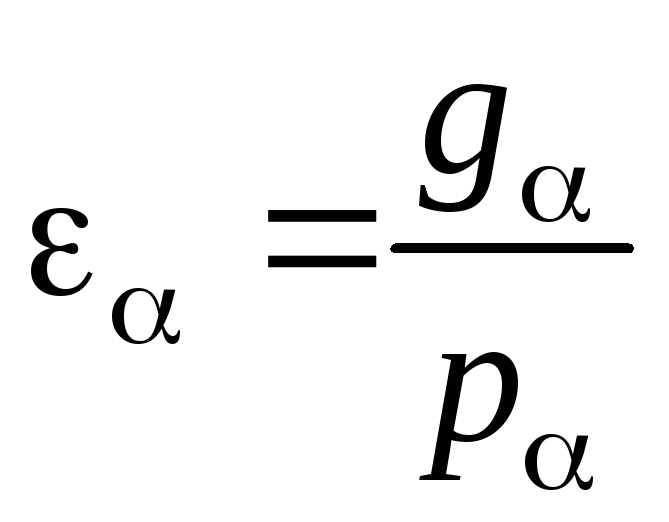. (3.97)

Активная линия зацепления – участок линии зацепления, в точках которого последовательно соприкасаются взаимодействующие профили зубьев. При отсутствии подрезания этот участок заключен между точками Н₁ и Н₂ (рис.3.46). Шагом зацепления р_ называется расстояние по контактной нормали (нормаль к главным профилям в точке их касания) между двумя контактными точками одноименных главных профилей соседних зубьев:

р_ =mcos. (3.98)

Длина активной линии зацепления g_:

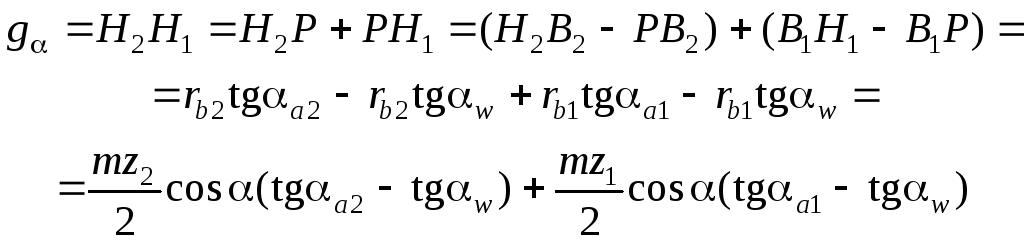
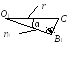
Здесь радиус основной окружности r_b получен из прямоугольного треугольника (рис.3.47), где гипотенуза – радиус делительной окружности (r=mz/2), а прилежащий катет – радиус основной окружности:

. (3.99)

Окончательно

. (3.100)

Подставляя (3.98) и (3.100) в (3.97), получаем выражение для вычисления коэффициента торцового перекрытия:

. (3.101)

Д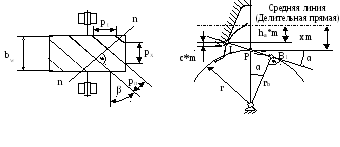ля прямозубых зубчатых колес обычно _ < 1,7. Для увеличения коэффициента перекрытия используют косозубые колеса, тогда добавляется коэффициент осевого перекрытия _, который может быть вычислен как отношение рабочей ширины венца передачи b_w к осевому шагу р_х (рис. 3.48):

, (3.102)

где m_n – расчетный или нормальный модуль, т.е. модуль в нормальном сечении nn.

3. Определим условие отсутствия подрезания в прямозубой эвольвентной передаче. На рис.3.49 изображено зацепление колеса с инструментальной рейкой (станочное зацепление) в момент, когда на линии зацепления РВ₁ располагается точка притупления прямолинейного профиля рейки и, следовательно, на зубчатом колесе формируется граничная точка L (граничная точка – общая точка эвольвентной части профиля зуба и переходной кривой). Средняя линия (делительная прямая) рейки не касается делительной окружности, а смещена относительно нее на расстояние, называемое смещением и выражаемое в долях модуля: хm, где х – коэффициент смещения. Смещение считается отрицательным, если делительная прямая рейки пересекает делительную окружность колеса.

Определим радиус кривизны _L эвольвенты в граничной точке.

. (3.103)

Для того, чтобы не было подрезания, надо, чтобы радиус кривизны эвольвенты был неотрицательным: _L  0. Из (3.103) следует, что

. (3.104)

При отсутствии смещения (х = 0) z_min = 17; при меньшем числе зубьев будет подрезание. Если же необходимо нарезать колесо с числом зубьев z < 17, то необходимо выполнить смещение инструмента при нарезании, причем наименьший коэффициент смещения x_min:

. (3.105)

4. Заострение зубьев возникает тогда, когда точка пересечения разноименных теоретических профилей зуба располагается внутри окружности вершин. Обычно принимают толщину зуба по дуге окружности вершин

(3.106)

для кинематических передач (т.е. для тех передач, которые не предназначены для передачи больших нагрузок) и

(3.106’)

для силовых.

5. Интерференция зубьев будет отсутствовать, если эвольвентный профиль зуба одного зубчатого колеса сопрягается только с эвольвентным профилем зуба другого колеса. Для этого необходимо, чтобы радиус граничной точки r_Li был меньше радиуса r_pi нижней точки активного профиля (рис.3.50):

i = 1, 2 (3.107)

При удовлетворении неравенства (3.107) для обоих зубчатых колес интерференция в зубчатой передаче отсутствует.

108