
§ 3. Многочлены на множестве комплексных чисел.
Определение 3.1. Многочленом n-ой степени (nN) от переменной х называется выражение вида
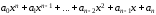 ,
,
где
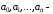 некоторые комплексные числа, называемые
коэффициентами многочлена, при этом
некоторые комплексные числа, называемые
коэффициентами многочлена, при этом
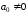 ,
а переменная х может принимать
произвольные (в том числе и комплексные)
значения.
,
а переменная х может принимать
произвольные (в том числе и комплексные)
значения.
Сумма, разность и произведение многочленов также являются многочленами.
Определение 3.2. Пусть даны два многочлена
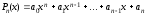 ,
,
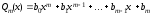 ,
,
причем
многочлен
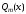 не равен тождественно нулю (и, таким
образом, не все его коэффициенты равны
нулю) и n
≥ m.
Если существует такой многочлен
не равен тождественно нулю (и, таким
образом, не все его коэффициенты равны
нулю) и n
≥ m.
Если существует такой многочлен
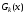 ,
что
,
что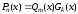 ,
то говорят, что многочлен
,
то говорят, что многочлен
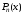 делится на
делится на
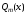 без остатка, при этом многочлен
без остатка, при этом многочлен
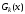 называется частным от деления
называется частным от деления
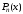 на
на
 .
Разделить многочлен
.
Разделить многочлен
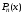 на
на
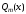 с остатком означает представить его в
виде
с остатком означает представить его в
виде
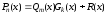 ,
где
,
где
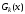 ,
,
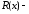 некоторые многочлены, причём многочлен
некоторые многочлены, причём многочлен
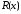 либо тождественно равен нулю, либо имеет
меньшую степень, чем многочлен
либо тождественно равен нулю, либо имеет
меньшую степень, чем многочлен
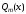 .
При этом многочлен
.
При этом многочлен
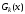 называется частным, а
называется частным, а
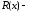 остатком от деления
остатком от деления
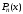 на
на
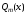 .
.
Теорема 3.1 (теорема Безу). Остаток
от деления многочлена
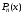 на разность
на разность
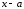 равен значению многочлена в точке а,
то есть
равен значению многочлена в точке а,
то есть
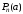 .
.
Определение 3.3. Уравнение
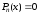 ,
где
,
где
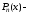 многочлен степени п, называется
алгебраическим уравнением п-ой
степени. Число
многочлен степени п, называется
алгебраическим уравнением п-ой
степени. Число
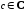 ,
при котором
,
при котором
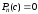 ,
называется корнем этого уравнения или
корнем многочлена
,
называется корнем этого уравнения или
корнем многочлена
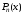 .
.
Теорема 3.2 (следствие из теоремы
Безу). Если а – корень многочлена
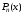 ,
то многочлен
,
то многочлен
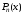 делится
на двучлен (
делится
на двучлен (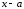 )
без остатка.
)
без остатка.
Теорема 3.3. Если аС
– корень многочлена с вещественными
коэффициентами
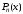 и
и
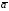 С
– число, комплексно сопряжённое с a,
то
С
– число, комплексно сопряжённое с a,
то
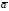 тоже корень данного многочлена.
тоже корень данного многочлена.
Теорема 3.4 (основная теорема
алгебры). Любой многочлен
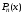 ,
степень которого
,
степень которого
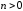 ,
имеет, по крайней мере, один корень (в
общем случае комплексный).
,
имеет, по крайней мере, один корень (в
общем случае комплексный).
Теорема 3.5. Любой многочлен
 ,
,
где
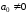 ,
на множестве комплексных чисел можно
представить в виде разложения:
,
на множестве комплексных чисел можно
представить в виде разложения:
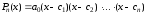 , (3.1)
, (3.1)
которое является единственным с точностью
до порядка сомножителей. Числа
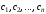 – все возможные (в том числе и комплексные)
корни многочлена
– все возможные (в том числе и комплексные)
корни многочлена
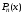 ,
других корней этот многочлен не имеет.
,
других корней этот многочлен не имеет.
Замечание 3.1. Среди чисел
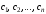 могут встречаться одинаковые. Такие
корни называются кратными.
могут встречаться одинаковые. Такие
корни называются кратными.
Определение 3.4. Число с
называется корнем многочлена
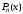 кратности k, если
кратности k, если
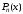 можно представить в виде:
можно представить в виде:
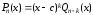 ,
причем
,
причем
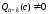 .
.
Замечание 3.2. Из теоремы 3.5 следует, что всякий многочлен n-ой степени на множестве комплексных чисел имеет ровно п корней с учётом кратности.
Для многочлена
 с действительными коэффициентами
равенство (3.1) можно преобразовать в так
называемое разложение на неприводимые
множители на множестве действительных
чисел. Любому комплексному корню такого
многочлена соответствует комплексно
сопряжённый корень (теорема 3.3). Перемножив
в равенстве (3.1) скобки, соответствующие
комплексно сопряжённым корням, приходим
к разложению
с действительными коэффициентами
равенство (3.1) можно преобразовать в так
называемое разложение на неприводимые
множители на множестве действительных
чисел. Любому комплексному корню такого
многочлена соответствует комплексно
сопряжённый корень (теорема 3.3). Перемножив
в равенстве (3.1) скобки, соответствующие
комплексно сопряжённым корням, приходим
к разложению
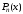 на линейные и квадратичные множителей
с действительными коэффициентами.
Квадратичные множители в полученном
соотношении будут иметь отрицательные
дискриминанты и, следовательно, не могут
быть разложены на линейные множители
на множестве действительных чисел.
Описанное разложение называется
разложением многочлена с действительными
коэффициентами на неприводимые
множители.
на линейные и квадратичные множителей
с действительными коэффициентами.
Квадратичные множители в полученном
соотношении будут иметь отрицательные
дискриминанты и, следовательно, не могут
быть разложены на линейные множители
на множестве действительных чисел.
Описанное разложение называется
разложением многочлена с действительными
коэффициентами на неприводимые
множители.
Пример 3.1. Разложить на R на
неприводимые множители двучлен
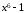 .
.
►1-й способ.
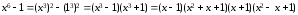 .
.
2-й способ. Найдём все (и комплексные
в том числе) корни двучлена
 .
Для этого решим уравнение
.
Для этого решим уравнение
 ,
отсюда
,
отсюда
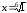 .
Для вычисления всех 6 значений
.
Для вычисления всех 6 значений
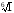 можно воспользоваться формулой (2.5),
предварительно записав число 1 в
тригонометрической форме:
можно воспользоваться формулой (2.5),
предварительно записав число 1 в
тригонометрической форме:
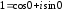 .
Однако, в таких простых случаях значения
корня можно получить, используя их
расположение на комплексной плоскости.
В данном случае значения
.
Однако, в таких простых случаях значения
корня можно получить, используя их
расположение на комплексной плоскости.
В данном случае значения
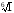 расположены в вершинах правильного
шестиугольника, одна из вершин которого
находится в точке (1, 0), так как х1=1–
одно из значений
расположены в вершинах правильного
шестиугольника, одна из вершин которого
находится в точке (1, 0), так как х1=1–
одно из значений
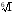 (рис. 3.1). Для х2 имеем равенство:
(рис. 3.1). Для х2 имеем равенство:
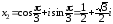 .
.
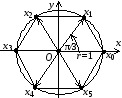
Рис. 3.1. К примеру 3.1.
Остальные значения
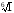 получим, используя симметрию их
расположения на комплексной плоскости:
получим, используя симметрию их
расположения на комплексной плоскости:
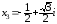 ,
,
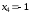 ,
,
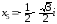 ,
,
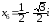 .
.
По теореме 3.5 данный двучлен представим в виде следующего произведения:
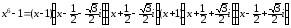 .
.
Отсюда, перемножив скобки с комплексно сопряжёнными корнями, получаем разложение
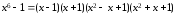 .◄
.◄
Пример 3.2. Составить многочлен
пятой степени с вещественными
коэффициентами, который делится без
остатка на двучлен
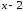 ,
а также имеет корни
,
а также имеет корни
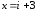 кратности 1 и
кратности 1 и
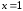 кратности 2, коэффициент при старшей
степени многочлена равен 1.
кратности 2, коэффициент при старшей
степени многочлена равен 1.
►Обозначим искомый многочлен через
P5(x). Он делится без остатка
на разность
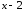 по условию, а также на
по условию, а также на
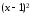 ,
поскольку имеет корень
,
поскольку имеет корень
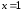 кратности 2 (определение 3.4). Следовательно,
P5(x) можно представить в
виде: P5(x) = (
кратности 2 (определение 3.4). Следовательно,
P5(x) можно представить в
виде: P5(x) = (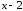 )
)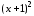 Q2(x),
где Q2(x) – некоторый
многочлен второй степени. Искомый
многочлен имеет корень
Q2(x),
где Q2(x) – некоторый
многочлен второй степени. Искомый
многочлен имеет корень
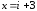 кратности 1, поэтому по теореме 3.3 число
кратности 1, поэтому по теореме 3.3 число
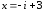 также является его корнем кратности 1,
следовательно, данный многочлен должен
делиться без остатка на произведение
также является его корнем кратности 1,
следовательно, данный многочлен должен
делиться без остатка на произведение
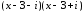 ,
которое после раскрытия скобок принимает
вид
,
которое после раскрытия скобок принимает
вид
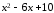 (это и есть Q2(x)). Итак, для
многочлена P5(x) получено
разложение:
(это и есть Q2(x)). Итак, для
многочлена P5(x) получено
разложение:
P5(x)
= (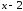 )
)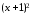
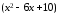 .
.
Раскрывая скобки, получаем многочлен,
удовлетворяющий условиям примера: P5(x)
=
 .◄
.◄
