
Комплексные числа и многочлены
I. Методические указания и примеры
§1. Действия с комплексными числами в алгебраической форме
Комплексными числами называются всевозможные упорядоченные пары
(x, y) действительных чисел, для которых следующим образом определены операции сложения и умножения:
 , (1.1)
, (1.1)
 . (1.2)
. (1.2)
Комплексное число принято обозначать буквой z, таким образом, z = (x, y). Действительные числа х и у называются действительной и мнимой частями комплексного числа z = (x, y) и обозначаются символами Re z и Im z.
Множество всех комплексных чисел обозначается C.
Два комплексных числа z1 = (x1, y1) и z2 = (x2, y2) называются равными в том и только в том случае, когда x1 = x2 и у1 = у2.
Из правил (1.1) – (1.2) сложения и умножения комплексных чисел следует, что любое комплексное число z = (x, y) можно записать в виде
z = (x, 0) +(0, 1)∙(y, 0). (1.3)
Числа (x, 0) и (y, 0) отождествляют с действительными числами x и y, а число (0, 1) обозначают через i (от французского слова imaginaire – мнимый). Равенство (1.3) перепишем теперь в виде:
 . (1.4)
. (1.4)
Равенство (1.4) называют алгебраической
формой комплексного числа. Заметим, что
из (1.2) следует
 .
.
Комплексное число
 называется комплексно сопряжённым
с числом
называется комплексно сопряжённым
с числом
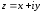 .
.
Деление комплексных чисел z1 = (x1, y1) и z2 = (x2, y2) выполняется с помощью формулы:
 .
.
Модулем комплексного числа z =
(x, y) называется действительное
число, равное
 и обозначаемое | z |.
Таким образом, | z |=
и обозначаемое | z |.
Таким образом, | z |= .
.
При сложении и умножении комплексных
чисел, представленных в алгебраической
форме, с ними можно обращаться как с
биномами вида x + iy, учитывая
дополнительно, что
 .
Для третьей и четвёртой степени числа
i справедливы равенства:
.
Для третьей и четвёртой степени числа
i справедливы равенства:
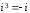 ,
,
 ,
действительно,
,
действительно,
 ,
,
 .
.
Пример 1.1. Вычислить:
 и записать в алгебраической форме.
и записать в алгебраической форме.
►Умножим числитель и знаменатель
первого слагаемого на число
 ,
сопряжённое знаменателю:
,
сопряжённое знаменателю:
 .
.
Вычисляя
 ,
имеем
,
имеем
 ,
,
 следовательно,
следовательно,
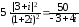 .
Умножим числитель и знаменатель последней
дроби на число, сопряжённое числу –3 +
4i, получим:
.
Умножим числитель и знаменатель последней
дроби на число, сопряжённое числу –3 +
4i, получим:
 .
.
Так как
 ,
то данное выражение будет равно:
,
то данное выражение будет равно:
 .◄
.◄
§ 2. Действия с комплексными числами, записанными в тригонометрической форме.
Рис. 2.1.
Геометрическая интерпретация комплексного
числа
 можно поставить в соответствие некоторую
точку М с абсциссой х и ординатой
у. При этом говорят, что точка М(х,
у) изображает комплексное число
можно поставить в соответствие некоторую
точку М с абсциссой х и ординатой
у. При этом говорят, что точка М(х,
у) изображает комплексное число
 .
Плоскость, на которой изображаются
комплексные числа, называется комплексной
плоскостью, ось Ох – действительной
осью, а ось Оу –мнимой осью. Модуль
комплексного числа геометрически
интерпретируется как расстояние точки
М, изображающей это число, до начала
координат, т. е. | z |
= r– длина радиус-вектора
.
Плоскость, на которой изображаются
комплексные числа, называется комплексной
плоскостью, ось Ох – действительной
осью, а ось Оу –мнимой осью. Модуль
комплексного числа геометрически
интерпретируется как расстояние точки
М, изображающей это число, до начала
координат, т. е. | z |
= r– длина радиус-вектора
 (рис. 2.1). Любое решение системы уравнений
(рис. 2.1). Любое решение системы уравнений
 ,
,
 (2.1)
(2.1)
называется аргументом комплексного
числа
 .
Все аргументы числа z различаются
на
.
Все аргументы числа z различаются
на
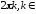 Z
и обозначаются единым символом
Z
и обозначаются единым символом
 .
Каждое значение
.
Каждое значение
 совпадает с величиной φ некоторого
угла, на который следует повернуть ось
Ox до совпадения с радиус-вектором
совпадает с величиной φ некоторого
угла, на который следует повернуть ось
Ox до совпадения с радиус-вектором
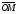 точки M (при этом φ > 0,
если поворот совершается против часовой
стрелки, и φ < 0
в противном случае). Значение
точки M (при этом φ > 0,
если поворот совершается против часовой
стрелки, и φ < 0
в противном случае). Значение
 :
:
 ,
называется главным значением и
обозначается символом
,
называется главным значением и
обозначается символом
 .
В некоторых случаях главным значениям
аргумента называется значение
.
В некоторых случаях главным значениям
аргумента называется значение
 :
:
 .
.
Из соотношений (2.1) следует, что для всякого комплексного числа z справедливо равенство
z , (2.2)
, (2.2)
называемое тригонометрической формой комплексного числа. Очевидно, φ и r являются полярными координатами точки, изображающей данное комплексное число z на комплексной плоскости (рис. 2.1).
Пусть два отличных от нуля комплексных числа z1 и z2 заданы в тригонометрической форме:
 ,
,
 .
.
Для произведения и частного чисел z1 и z2 справедливы следующие формулы:
 , (2.3)
, (2.3)
 . (2.4)
. (2.4)
Из соотношений (2.3) и (2.4) следует равенство:
 ,
,
справедливое при любых целых n. Оно называется формулой Муавра и позволяет возводить комплексное число в любую целую степень, записав его в тригонометрической форме. Для корня n-ой степени из комплексного числа z, записанного в тригонометрической форме (2.2), справедливо равенство:
 ,
n
,
n N,
k = 0, 1, 2, ... , n – 1. (2.5)
N,
k = 0, 1, 2, ... , n – 1. (2.5)
Рис. 2.2. Расположение
значений корня n-ой
степени из комплексного числа на
комплексной плоскости
 (имеется в виду арифметическое значение
корня степени
(имеется в виду арифметическое значение
корня степени
 из положительного числа r),
все они лежат на окружности радиуса
из положительного числа r),
все они лежат на окружности радиуса
 с центром в точке
с центром в точке
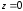 и делят эту окружность на
и делят эту окружность на
 равных дуг, т.е. являются вершинами
правильного n-угольника
(рис. 2.2).
равных дуг, т.е. являются вершинами
правильного n-угольника
(рис. 2.2).
Пример 2.1. Изобразить множество точек комплексной плоскости, удовлетворяющих следующим условиям:

►Множество, описываемое первым неравенством, есть часть комплексной плоскости, покрываемая лучами, исходящими из точки (0, 0) и имеющими всевозможные углы наклона к вещественной оси из промежутка (–π/3; π/3) (рис. 2.3а).
|
|
|
|
|
|
а) |
б) |
в) |
г) |
|
Рис. 2.3. К примеру 2.1 |
|||
Чтобы построить множество, описываемое
вторым неравенством, запишем число z
в алгебраической форме: z =
x +
iy. Имеем |
z–1| = |
(x –
1)+ iy
| =
= ,
отсюда
,
отсюда
 или
или
 .
Итак, множество, описываемое вторым
неравенством, есть часть комплексной
плоскости, находящаяся внутри круга
радиуса 3 и центром в точке А(1, 0)
(рис. 2.3б). Множество, описываемое третьим
неравенством, состоит из тех точек
комплексной плоскости, абсциссы которых
больше 1 (рис. 2.3в). Таким образом, искомое
множество состоит из тех и только тех
точек плоскости, которые принадлежат
одновременно трём построенным областям
(рис. 2.3г).◄
.
Итак, множество, описываемое вторым
неравенством, есть часть комплексной
плоскости, находящаяся внутри круга
радиуса 3 и центром в точке А(1, 0)
(рис. 2.3б). Множество, описываемое третьим
неравенством, состоит из тех точек
комплексной плоскости, абсциссы которых
больше 1 (рис. 2.3в). Таким образом, искомое
множество состоит из тех и только тех
точек плоскости, которые принадлежат
одновременно трём построенным областям
(рис. 2.3г).◄
Rez
Rez
Пример 2.2. Вычислить
 .
.

Рис. 2.4. К примеру 2.2.
►Число под знаком корня запишем в тригонометрической форме:
 ,
где
,
где
 ,
,
 и воспользуемся формулой (2.5):
и воспользуемся формулой (2.5):
 =
=
=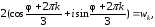
 По известным sinφ и cosφ находим, что
По известным sinφ и cosφ находим, что
 .
.
Придавая k последовательно значения 0, 1, 2, получаем все значения корня:
k=0
 ,
,
k=1
 ,
,
k=2
 .
.
Значения косинусов
и синусов углов
 и
и
 найдены с помощью формул и формул
половинных углов, известных из
тригонометрии. Например,
найдены с помощью формул и формул
половинных углов, известных из
тригонометрии. Например,
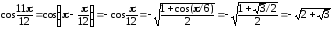 .
.
На комплексной
плоскости точки, изображающие значения
корня
 ,
являются вершинами правильного
треугольника (рис. 2.4). ◄
,
являются вершинами правильного
треугольника (рис. 2.4). ◄




