3.2 Микроскопическая теория

Из теории диэлектриков известно, что внутренние электрическое поле, действующее на атом или ион в твердом теле, существенно отличается от внешнего электрического поля, приложенного к телу. В этой теории исходят из того, что каждый атом или ион имеет микроскопические размеры и его смещение или (и) деформация определяется силой, обусловленной микроскопическим полем в точке расположения атома (иона), за вычетом вклада в это поле, вносимого самим атомом (ионом). Такое поле называют локальным или эффективным с напряженностью Е_лок. При расчете этого поля учитывается поля всех зарядов, за вычетом поля в рассматриваемой точке.

Обычно локальное поле находится следующим образом. Вокруг данного атома мысленно проводят сферу. Идея ее введения заключается в том, что поле диполей внутри сферы вычисляется с учетом дискретной структуры кристалла, а в остальной части образца – макроскопически, с помощью эффективных поверхностных зарядов в предположении непрерывности среды.

Наиболее просто Е_лок можно рассчитать методом Лоренца. Для этого все пространство кристалла разбивают на ближнюю и дальнюю от данной точки А области (рис 3.3)[4].

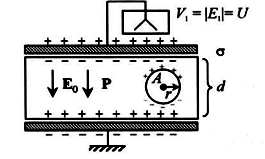
Рис. 3.3. Схематическое изображение поляризации диэлектриков согласно микроскопической теории

Ближняя представляет собой сферу радиуса r вокруг точки А, внутри которой локальное поле вычисляется с учетом дискретной структуры кристалла. Дальняя область содержит все внешние источники поля, все точки вне кристалла и те точки внутри него, расстояние до которых от точки А велико по сравнению с размером сферы Лоренца. При таком рассмотрении микроскопическое поле, создаваемое зарядами из дальней области, равно своему макроскопическому среднему значению, поэтому диполи, расположенные внутри сферы Лоренца, учитываются каждый в отдельности, а вклад всего остального объема кристалла вне поверхности сферы дается в приближении континуума.

Таким образом, локальное поле на атоме в диэлектрике, возникающее под влиянием внешних зарядов, можно представить как векторную сумму полей:

Е_лок=Е₀+Е_деп+Е_пов+Е_дип, (3.16)

где Е₀ – внешнее электрическое поле ( точнее, его напряженность);

Е_деп - деполяризирующее поле (обратное по знаку внешнему полю), возникающее от зарядов, появившихся на внешней поверхности образца при его поляризации (Е₀+ Е_деп=Е₁, где Е₁ – среднее поле, величина которого соответствует u/d (рис. 3.3));

E_пов - лоренцево поле, образованное связанными зарядами (не способными перемещаться на микроскопические расстояния) на поверхности воображаемой сферы;

Е_дип – поле атомов внутри сферической плоскости, возникающее под влиянием отдельных диполей, которые расположены по всем атомным узлам внутри сферы, исключая один центральный. Оно вычисляется тем точнее, чем больше соседей учтено, т.е. чем больше будет радиус сферы.

На основании вышеизложенного имеем:

Е_лок=Е₁+Е_пов+Е_дип. (4.17)

Влияние поверхностных зарядов можно учесть путем суммирования по поверхности сферы. Переходя от суммирования к интегрированию, получаем Е_пов=Р/3ε₀. В изотропных средах и в диэлектриках с простой кубической решеткой Е_дип=0, и как следствие равенство (3.17) можно представить в виде:

(3.17а)

С учетом (4.3) и (4.5) получаем

Р= ε₀(ε-1)Е. (3.18)

Подставляя это равенство в (1.17а), находим, что в атомном узле кубической решетки при Е₁=Е

(3.19)

Если введем в это равенство поляризуемость частиц α_п, которая связана с вектором Р соотношением:

Р=Nα_пЕ_лок, (3.20)

(где N – число частиц данного сорта в 1 см³), то с учетом (1.18)-(1.20) получим откуда

(3.21)

где (N_a – число Авогадро, М – молекулярная масса вещества, ρ – его плотность). Это соотношение называют уравнением Клазиуса-Мосотти. Оно связывает между собой макро- (ε) и микроскопическую (α_п) характеристики поляризации изотропных диэлектриков[11].

4 ОСОБЕНОСТИ ДОМЕННОЙ СТРУКТУРЫ СЕГНЕТОЭЛЕКТРИКОВ