3 Макроскопическая и микроскопическая теории диэлектриков

3.1 Макроскопическая теория

Диэлектрические свойства материала определяют по его поведению в поле плоскостного конденсатора. Если диэлектрик толщиной d поместить между обкладками конденсатора (рис.3.1) и подать на них напряжение U, то под действием электрического поля будет происходить перераспределение электронной плоскости за счет смещения электрических зарядов и диэлектрик начнет поляризоваться. При этом напряженность электрического поля, очевидно, будет почти постоянной и равной

. (3.1)

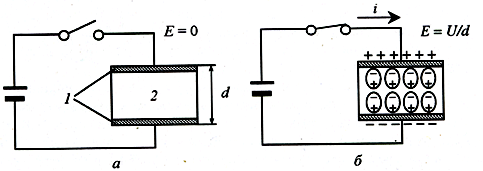
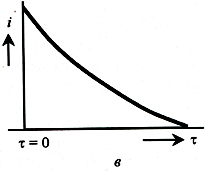
Рис 3.1 - Поведение диэлектрика в электрическом поле: 1 – электроды, 2 – диэлектрик

В момент приложения электрического поля протекает зарядный ток (рис. 3.1,в), который создается поляризационными процессами образования дипольных моментов. В результате поляризации на поверхности диэлектрика появляются заряды, противоположные по знаку свободным зарядам.

Количественно поляризацию диэлектрика характеризуют дипольным моментом единицы объема, называемым вектором поляризации Р.

. (3.2)

где p_i - дипломные моменты частиц (атомов, ионов, молекул);

N – число частиц в объеме V. Величина Р зависит то напряженности Е электрического поля, вызывающего в диэлектрике электрическую индукцию. Если электрик изотропен (рис. 3.2,а), то вектор D параллелен вектору Е, в случае анизотропного диэлектрика направления векторов Р и Е не совпадают, т.е. заряды в нем смещаются от направления приложенного поля (рис. 3.2,б).

Рис. 3.2. Соотношение между векторами в изотропным (а) и анизотропном (б) телах в прямоугольной системе координат (1,2,3)

Для анизотропных диэлектриков, где векторы Р и Е коллинеарны в слабых полях:

ε₀œ_вЕ,

где œ_в – диэлектрическая восприимчивость, характеризующая способность тела к поляризации; ε₀ – диэлектрическая постоянная вакуума[4].

ε₀=8,85∙10¹²Кл/(В∙м). Направление вектора Р внутри диэлектрика выбирают от отрицательно заряженной поверхности к положительно заряженной.

Между векторами электрической индукции (смещения) D,P и Е существует следующая связь:

D=ε₀Е+P= ε₀εE, (3.4)

где – диэлектрическая проницаемость, характеризующая поляризацию диэлектриков под действием электрического поля,

ε=1+œ_e. (3.5)

Величина ε показывает, во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме. Ослабление взаимодействия происходит из-за экранизации свободных зарядов связанными, образующимся в результате поляризации среды. Как и œ_е, величина ε скалярна в изотропных диэлектриках и является тензором в анизотропных, т.е. векторы D,P и Е последних не совпадают ни по величине, ни по направлению (рис. 4.2,б). Параметры ε и œ – основные характеристики диэлектрика[4].

Если в анизотропном диэлектрике связь между D и Е линейна, его температура постоянна, а внешнее поле статическое, то в кристаллографической системе координат между составляющими векторов D и Е имеет место следующая зависимость:

D_i=ε_ijE_j, i,j=1,2,3, (3.6)

где, как всегда в тензорных обозначениях, подразумевается суммирование по повторяющемуся индексу.

Для того чтобы определить диэлектрическую проницаемость анизотропного тела, необходимо задать девять коэффициентов ε_ij, которые являются тензором второго ранга. На практике в силу симметрии среды отдельные компоненты тензора ε_ij обращаются в ноль или равны друг другу. Например, для пьзокерамики (предельная точечная группа ∞mm, ось 3 соответствует направлению остаточной поляризации) компоненты тензора E_ij представляюся матрицей:

(3.7)

и имеет смысл различать лишь две компоненты диэлектрической проницаемости: ε₃₃ – в направлении поляризации и ε₁₁ – в плоскости, перпендикулярной поляризации.

Электрические свойства сегнетоэлектриков зависят от их механического состояния. Для учета этого обстоятельства верхними индексами обозначают постоянство (обычно равенство нулю) механического напряжения Т или деформации S. Таким образом, обозначения ε^Т₃₃ и ε^S₃₃ показывают диэлектрическую проницаемость вдоль полярной оси соответственно механически зажатого образцов.

Часто рассматривают безразмерную относительную диэлектрическую проницаемость:

ε _r= ε/ ε_0. (3.8)

При действии переменного поля поляризационный заряд имеет как синфазную, так и сдвинутую по фазе 90⁰ составляющие, обусловленные потерями энергии. Это позволяет рассматривать диэлектрическую проницаемость как комплексную величину:

ε*= ε΄-iε˝. (3.9)

Безразмерное соотношение мнимой и вещественных составляющих

tgδ= ε˝/ ε΄ (3.10)

называется тангенсом угла диэлектрических потерь и характеризует все их виды. В сегнетоэлектрике величины ε и tgδ существенно зависят от амплитуды электрического поля[4].

Основной пьезокерамический параметр – пьезомодуль, связывающий поляризацию Р с механическим напряжением Т (прямой эффект) или деформацию S с приложенным полем Е. Поскольку Е и Р – векторы, а Т и S – тензоры второго ранга, пьезомодуль должен быть тензором третьего ранга и иметь 27 компонентов:

P_i=d_ijkT_jk; S_ij=d_ijkE_k. (3.11)

Симметричность тензоров T и S (T_jk=T_kj) снижает максимально возможное число компонент пьзомодуля до 18 и позволяет использовать для их обозначения двух индексную систему:

d_im, i=1,2,3; m=1,2,…,6. (3.12)

Два последующих индекса (jk) в тензорной записи заменяются одним по последующей схеме:

jk 11 22 33 23…32 31…13 12…21. (3.13)

m 1 2 3 4 5 6

В результате все компоненты пьзомодуля можно представить матрицей d_im порядка 3×6.

Симметрия кристалла сохраняет лишь некоторые различающиеся не нулевые компоненты. Например, пьезосвойства кварца можно описать всего двумя нулевыми компонентами:

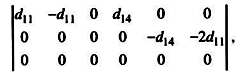(3.14)

а пьезосвойства полярной текстуры (пьезокерамики) – тремя:

(3.15)

Связь электрического поля вдоль полярной оси с продольной деформацией продольный пьезомодуль d₃₃ описывает в том же направлении, а поперечный d₃₁ – в любом из перпендикулярных направлений. Сдвиговый пьезомодуль d₁₅ связывает поле, направленное перпендикулярно к полярной оси со сдвиговой деформацией в плоскости, проходящей через полярную ось.

Другими важными параметрами пьезоэлектрика являются коэффициент электромеханической связи k_im (индексы те же, что у пьезомодуля) и механическая добротность Q_m. Первый из них характеризует пьезоэлемент вдали от частоты его собственного акустического резонанса. Величина равна той доли механической энергии, которая для данного типа колебаний преобразуется в электрическую, или наоборот. Остальная энергия пьзоэлементом не преобразуется, она запасается в виде упругой или электрической энергии заряженного конденсатора.

Механическая добротность Q_m характеризует пьнзоэлемент в резонансном режиме. Обратная величина 1/ Q_m показывает, какая часть включает в себя диэлектрические потери, пропорциональные tgδ, и потери упругой энергии на вязкое трение[4].