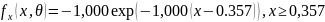МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
Лабораторная работа
«Экспериментальное определение закона распределения случайной величины»
Выполнил:
Студент группы 04-220
Игроков Л.А.
Проверил:
Рудненко А.В.
Москва 2011
Оглавление
Общие сведения по выполнению работы
Порядок выполнения работы
Общие сведения по выполнению работы Математическое ожидание
Рассмотрим случайную величину с числовыми значениями. Часто оказывается полезным связать с этой функцией число — её «среднее значение» или, как говорят, «среднюю величину», «показатель центральной тенденции». По ряду причин, некоторые из которых будут ясны из дальнейшего, в качестве «среднего значения» обычно используют математическое ожидание.
Математическим ожиданием случайной величины X называется число
,
то есть математическое
ожидание случайной величины — это
взвешенная сумма значений случайной
величины с весами, равными вероятностям
соответствующих элементарных событий.
Если случайная величина X принимает
значения
.
Тогда справедливо равенство
,
Пусть X — случайная величина, M(X) — её математическое ожидание, a — некоторое число. Тогда
M(a) = a;
;
.
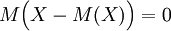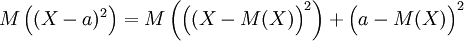Дисперсия случайной величины
Математическое
ожидание показывает, вокруг какой точки
группируются значения случайной
величины. Необходимо также уметь измерить
изменчивость случайной величины
относительно математического ожидания.
Выше показано, что
достигает
минимума по a при a = M(X).
Поэтому за показатель изменчивости
случайной величины естественно взять
именно
.
Дисперсией случайной величины X называется число
.
Установим ряд свойств дисперсии случайной величины, постоянно используемых в вероятностно-статистических методах принятия решений.
Пусть X — случайная величина, a и b — некоторые числа, Y = aX + b. Тогда
D(Y) = a2D(X).
.
Пусть
—
попарно независимые случайные величины
(то есть Xi и Xj
независимы, если
).
Пусть Yk — их сумма,
,
тогда дисперсия суммы равна сумме
дисперсий слагаемых,
.
Для любых случайкых величин математическое ожидание суммы равно сумме математических ожиданий слагаемых,
.
Хи-квадрат Пирсона.
С помощью нормального распределения определяются три распределения, которые в настоящее время часто используются при статистической обработке данных. В дальнейших разделах книги много раз встречаются эти распределения.
Распределение Пирсона χ2 (хи-квадрат) — распределение случайной величины
,
где случайные
величины
независимы
и имеют одно и тоже распределение N(0,1).
При этом число слагаемых, то есть n,
называется «числом степеней свободы»
распределения хи-квадрат.
Распределение хи-квадрат используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений, и во многих других задачах статистического анализа данных.
Порядок выполнения работы ее цель
Вариянт 1
Задание 1
По заданной сововкупности реализаций случайной величины Х построить параметритрическую оценку ее плотности и функции распределения
Задание 2
Исследовать влияние объемно выборки на точнойсть оценок и достоверность приянтых решений
Опыт 1
Ввели требуемое число реализаций:
20 <= n <= 200
Смоделировалась выборка состоящая из эллементов:
Вариационный ряд выборки
Общие Характеристики набора реализаций:
Число реализаций n=30
Минимальное значение Xmin= -2,8295
Максимальное значение Xmax= -0,7846
Задание:
Найти закон распределения исследуемой случайной величины, если известно, что он может быть:
Нормальным (гауссовским)
Равномерным на некотором интервале
Экспоненциальным
Оценка моментных характеристик случайной величины:
Оценка математического ожидания: -1,807
Оценка дисперсии: 0.348
Оценка среднего квадратического отклонения: 0.590
График:
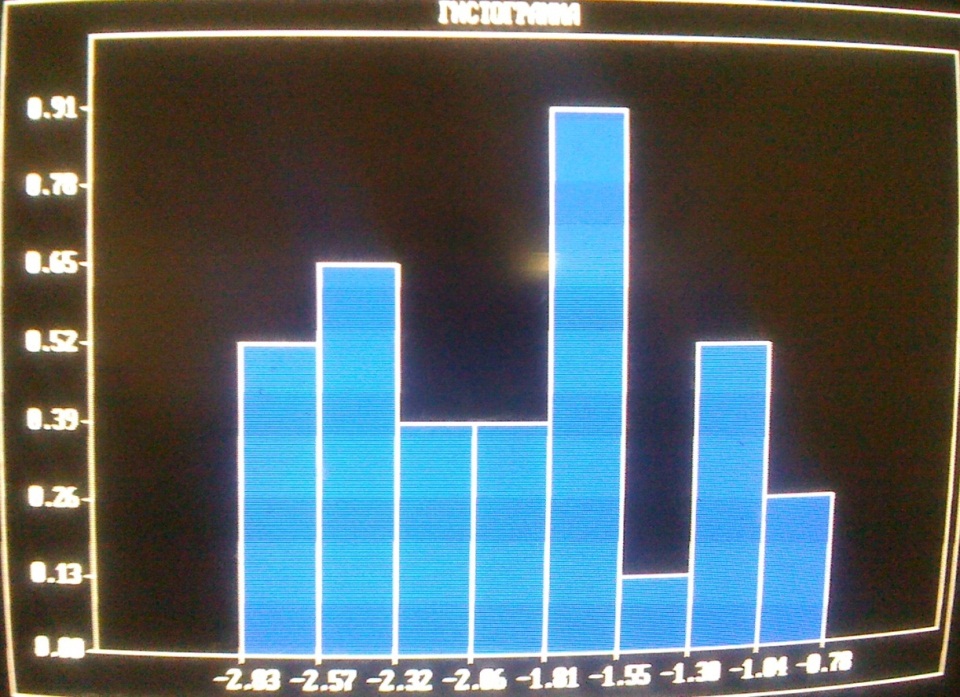
Таблица данных для построения гистограммы:
Интервал разбит [Xmin, Xmax] на 8 подинтервалов:
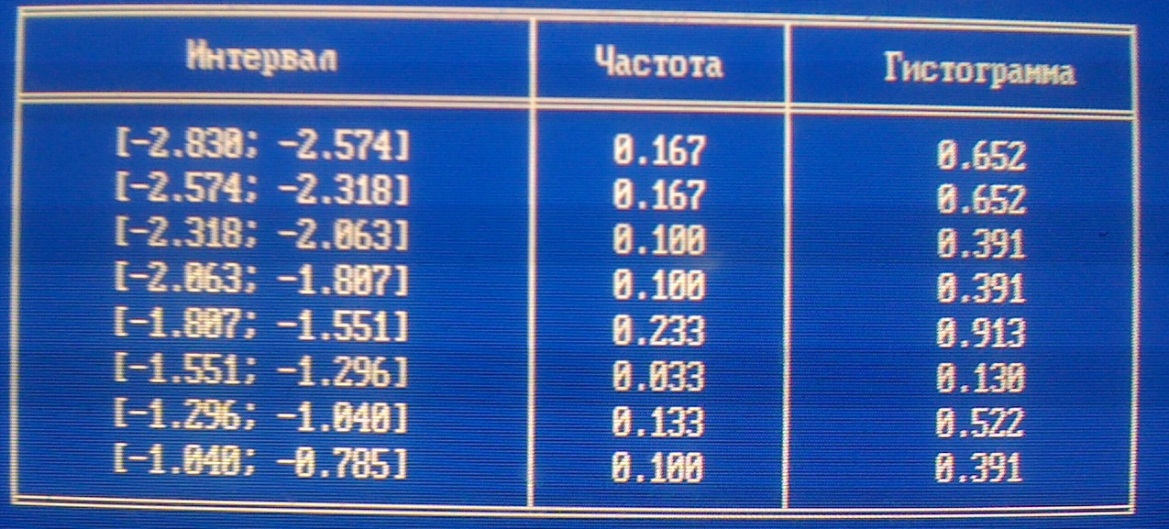
Для проверки предлагаются следущие гипотезы о законе распеределения случайной величины:
Гипотеза 1 нормальное распределение
Гипотеза 2 равномерное распределение
Гипотеза 3 экспоненциальное распределение
Введем номер наиболее правдоподобной гипотезы для ее проверки по критерики хи-квадрат Пирсона:
Гипотеза 1
Таблица вероятностей попадания в интервал:
Значение статистики критерия Пирсона: g=21,970
Число степеней свободы равно 7
Нельзя ли принять проверяемую гипотезу на уровне 0.05?
r |
P |
|||||||||||||
0,99 |
0,98 |
0,95 |
0,90 |
0,80 |
0,70 |
0,50 |
0,30 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
0,001 |
|
7 |
1,239 |
1,564 |
2,17 |
2,83 |
3,82 |
4,67 |
6,35 |
8,38 |
9,80 |
12,02 |
14,07 |
16,62 |
18,48 |
24,30 |
Из таблицы распределения хи-квадрат Пирсона можно увидеть, что данную гипотезу нельзя принять на уровне значимости 0.05, но можно принять на уровне значимости 0.001, т.к. 18,48<21,970<24,30. Проверим остальные гипотезы.
Проверяем гипотезу 2
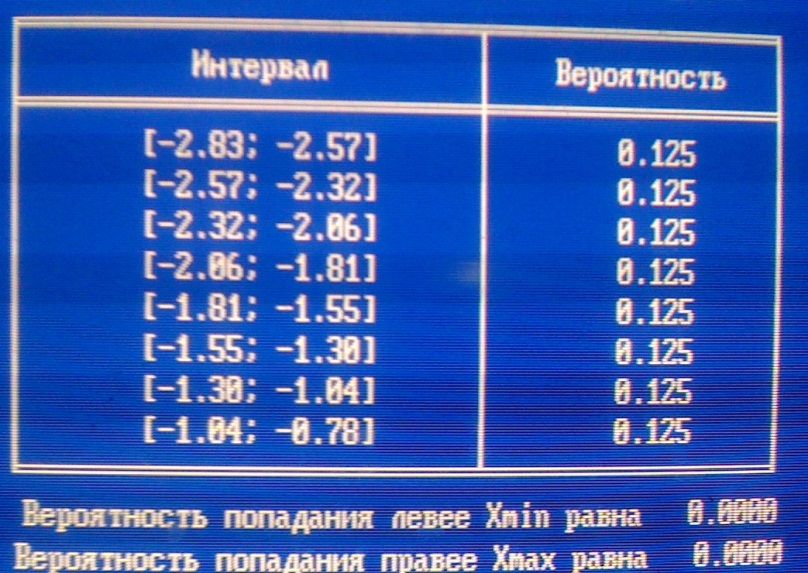
Значение статистики критерия Пирсона: g=6,133
Число степеней свободы равно 7
Нельзя ли принять проверяемую гипотезу на уровне 0.05?
r |
P |
|||||||||||||
0,99 |
0,98 |
0,95 |
0,90 |
0,80 |
0,70 |
0,50 |
0,30 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
0,001 |
|
7 |
1,239 |
1,564 |
2,17 |
2,83 |
3,82 |
4,67 |
6,35 |
8,38 |
9,80 |
12,02 |
14,07 |
16,62 |
18,48 |
24,30 |
Из таблицы распределения хи-квадрат Пирсона можно увидеть, что данную гипотезу нельзя принять на уровне значимости 0.05, но можно принять на уровне значимости 0.50, т.к. 4,67<6,133<24,30. Проверим остальные гипотезы.
Проверяем гипотезу 3:
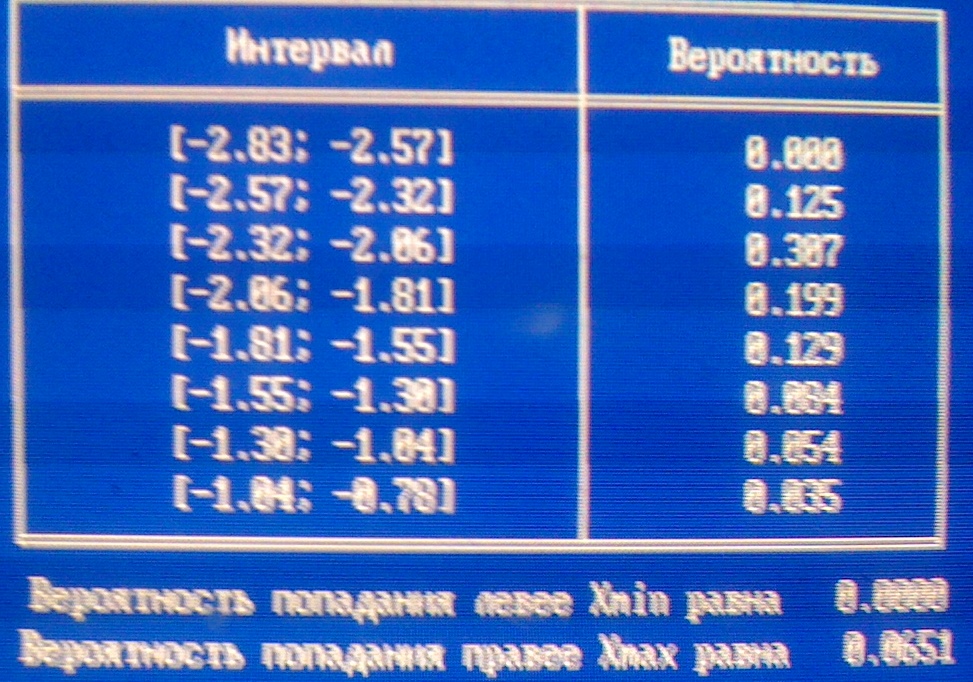
Значение статистики критерия Пирсона: g=30028,424
Число степеней свободы равно 7
Нельзя ли принять проверяемую гипотезу на уровне 0.05?
r |
P |
|||||||||||||
0,99 |
0,98 |
0,95 |
0,90 |
0,80 |
0,70 |
0,50 |
0,30 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
0,001 |
|
7 |
1,239 |
1,564 |
2,17 |
2,83 |
3,82 |
4,67 |
6,35 |
8,38 |
9,80 |
12,02 |
14,07 |
16,62 |
18,48 |
24,30 |
Из таблицы распределения хи-квадрат Пирсона можно увидеть, что данную гипотезу нельзя принять ни на каком уровне, т.к. 30028,424>24.30.
Опыт 2
Ввели требуемое число реализаций:
20 <= n <= 200
Смоделирована выборка состоящая из элементов:
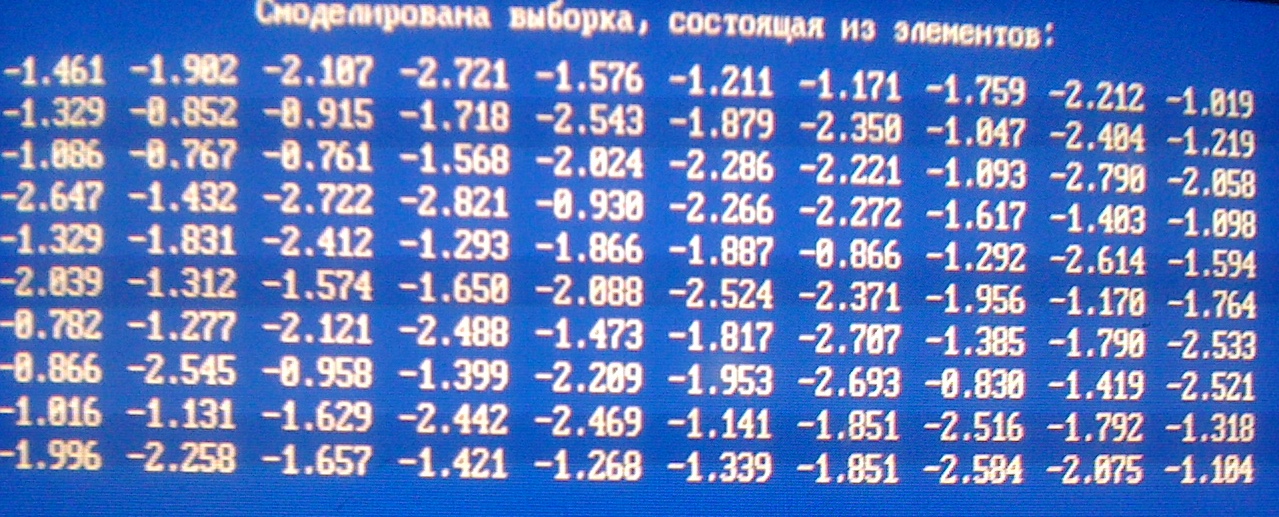
Вариационны ряд выборки:
Общие Характеристики набора реализаций:
Число реализаций n=100
Минимальное значение Xmin= -2,8210
Максимальное значение Xmax= -0,7614
Задание:
Найти закон распеределения исследуемой случайной величины, если известно, что он может быть:
Нормальным (гауссовским)
Равномерным на некотором интервале
Экспоненциальным
Оценка моментных характеристик случайной величины:
Оценка математического ожидания: -1,791
Оценка дисперсии: 0.353
Оценка среднего квадратического отклонения: 0.595
График:
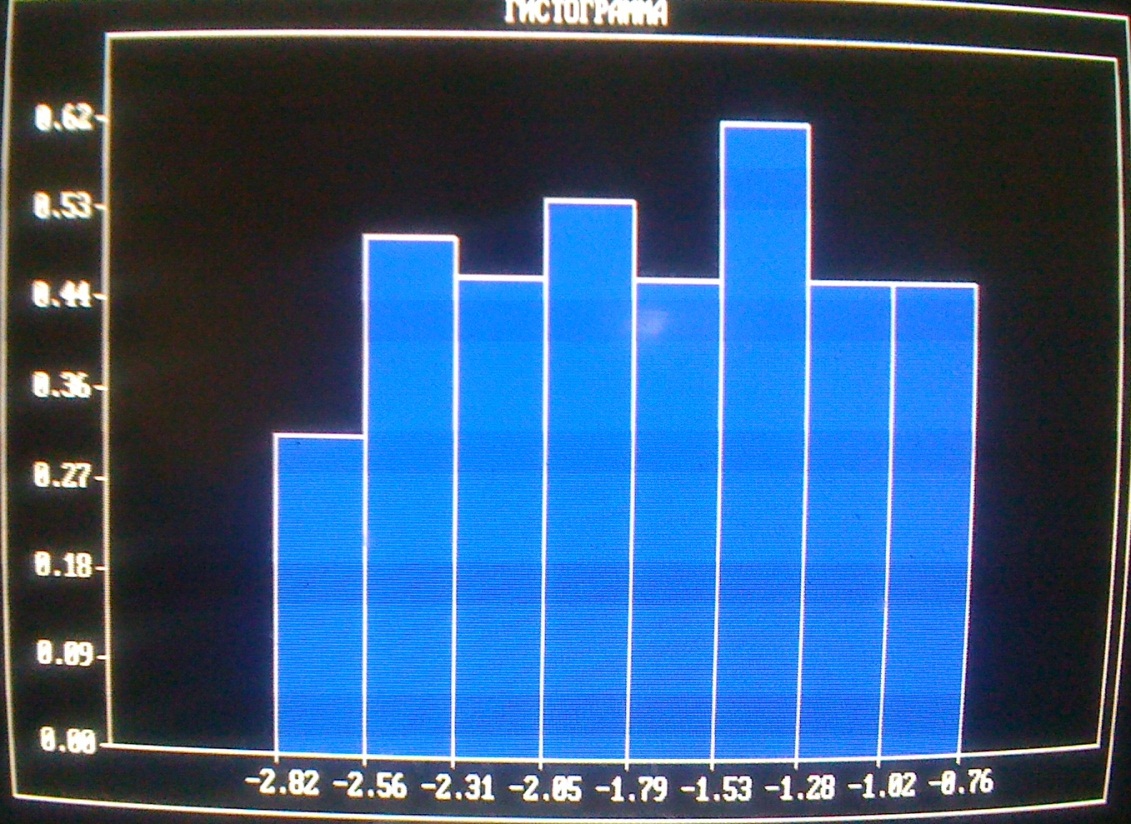
Таблица данных для построения гистограммы:
Интервал разбит [Xmin, Xmax] на 8 подинтервалов:
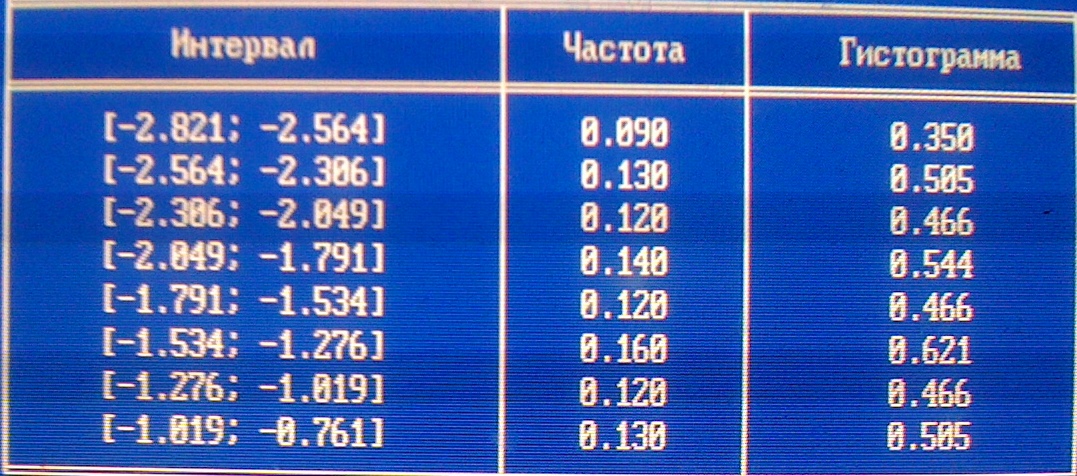
Для проверки предлагаются следущие гипотезы о законе распеределения случайной величины:
Гипотеза 1 нормальное распределение
Гипотеза 2 равномерное распределение
Гипотеза 3 экспоненциальное распределение
Введем номер наиболее правдоподобной гипотезы для ее проверки по критерики хи-квадрат Пирсона:
Гипотеза 1
Таблица вероятностей попадания в интервал:
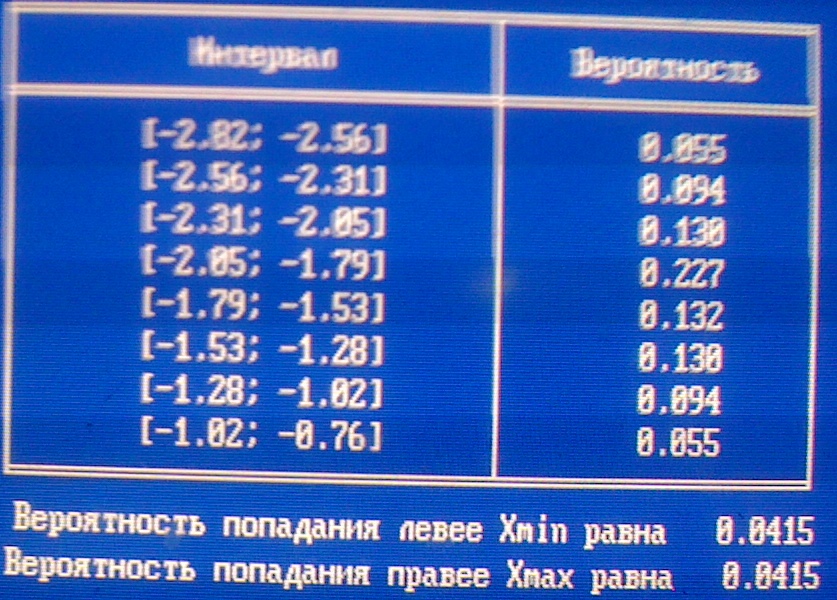
Значение статистики критерия Пирсона: g=35,489
Число степеней свободы равно 7
Нельзя ли принять проверяемую гипотезу на уровне 0.05?
r |
P |
|||||||||||||
0,99 |
0,98 |
0,95 |
0,90 |
0,80 |
0,70 |
0,50 |
0,30 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
0,001 |
|
7 |
1,239 |
1,564 |
2,17 |
2,83 |
3,82 |
4,67 |
6,35 |
8,38 |
9,80 |
12,02 |
14,07 |
16,62 |
18,48 |
24,30 |
Из таблицы распределения хи-квадрат Пирсона можно увидеть, что данную гипотезу нельзя принять ни на каком уровне, т.к. 35,489>24.30.
Проверяем гипотезу 2
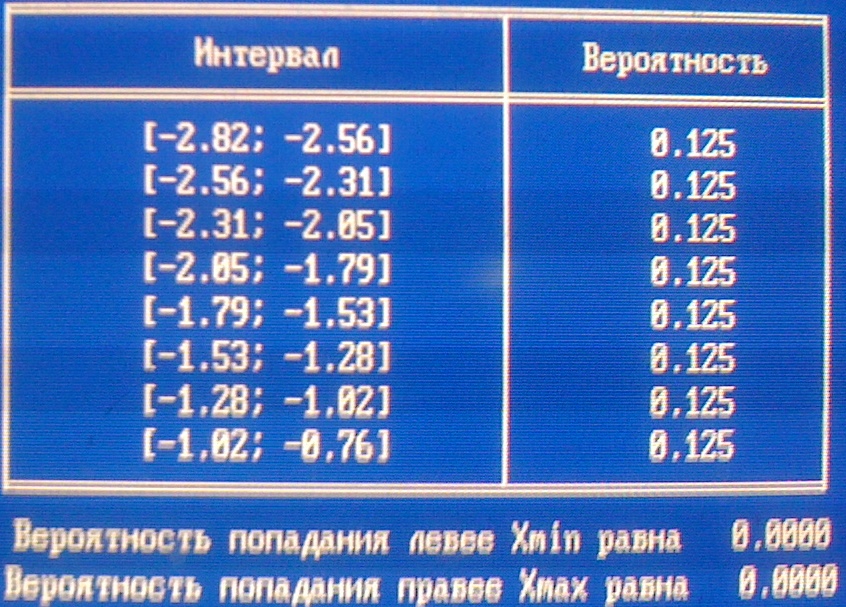
Значение статистики критерия Пирсона: g=2,240
Число степеней свободы равно 7
Нельзя ли принять проверяемую гипотезу на уровне 0.05?
r |
P |
|||||||||||||
0,99 |
0,98 |
0,95 |
0,90 |
0,80 |
0,70 |
0,50 |
0,30 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
0,001 |
|
7 |
1,239 |
1,564 |
2,17 |
2,83 |
3,82 |
4,67 |
6,35 |
8,38 |
9,80 |
12,02 |
14,07 |
16,62 |
18,48 |
24,30 |
Из таблицы распределения хи-квадрат Пирсона можно увидеть, что данную гипотезу нельзя принять на уровне значимости 0.05, но можно принять на уровне значимости 0.90, т.к. 2,17<2,240<2,83. Проверим остальные гипотезы.
Проверяем гипотезу 3
Значение статистики критерия Пирсона: g=100066,578
Число степеней свободы равно 7
Нельзя ли принять проверяемую гипотезу на уровне 0.05?
r |
P |
|||||||||||||
0,99 |
0,98 |
0,95 |
0,90 |
0,80 |
0,70 |
0,50 |
0,30 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
0,001 |
|
7 |
1,239 |
1,564 |
2,17 |
2,83 |
3,82 |
4,67 |
6,35 |
8,38 |
9,80 |
12,02 |
14,07 |
16,62 |
18,48 |
24,30 |
Из таблицы распределения хи-квадрат Пирсона можно увидеть, что данную гипотезу нельзя принять ни на каком уровне, т.к. 100066,578>24.30.
Опыт 3
Смоделирована выборка из элементов:
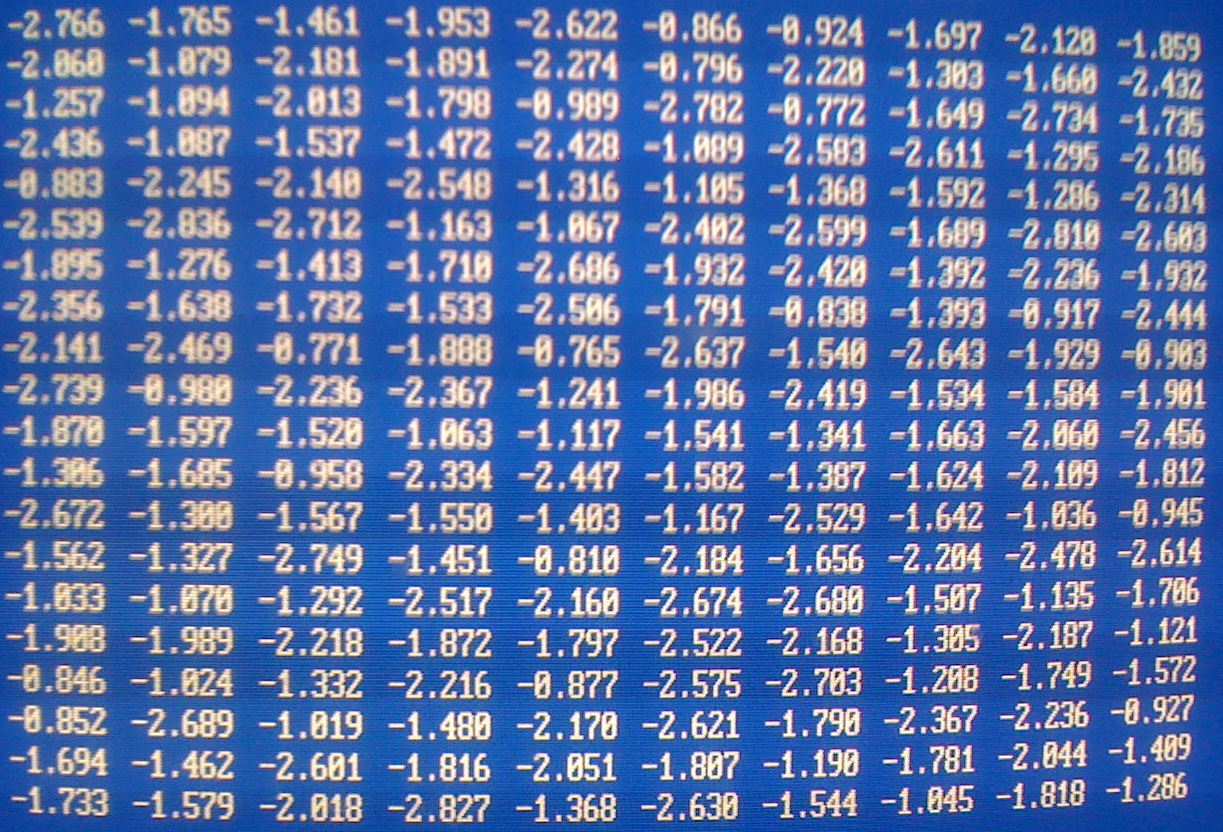
Вариационный ряд выборки:
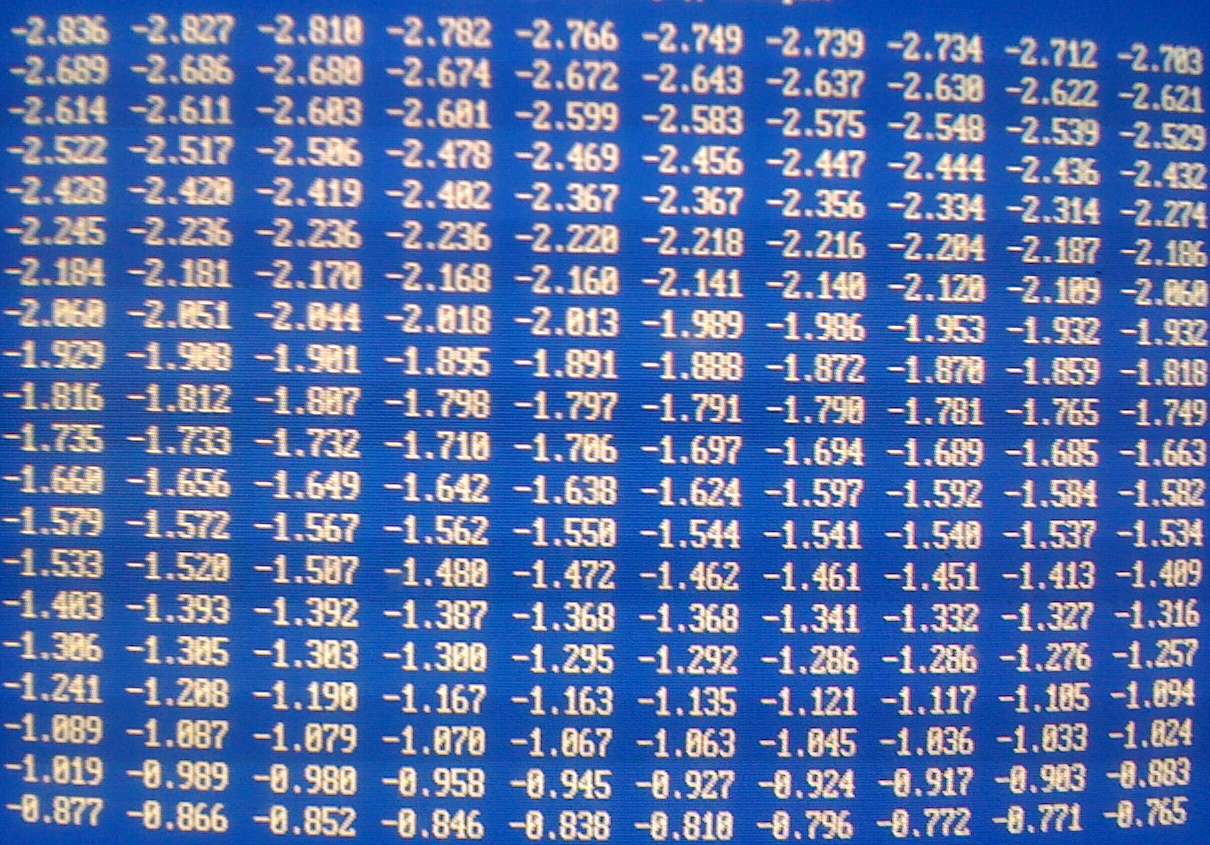
Общие Характеристики набора реализаций:
Число реализаций n=200
Минимальное значение Xmin= -2,8359
Максимальное значение Xmax= -0,7649
Задание:
Найти закон распеределения исследуемой случайной величины, если известно, что он может быть:
Нормальным (гауссовским)
Равномерным на некотором интервале
Экспоненциальным
Оценка моментных характеристик случайной величины:
Оценка математического ожидания: -1,000
Оценка дисперсии: 0.357
Оценка среднего квадратического отклонения: 0.598
График:
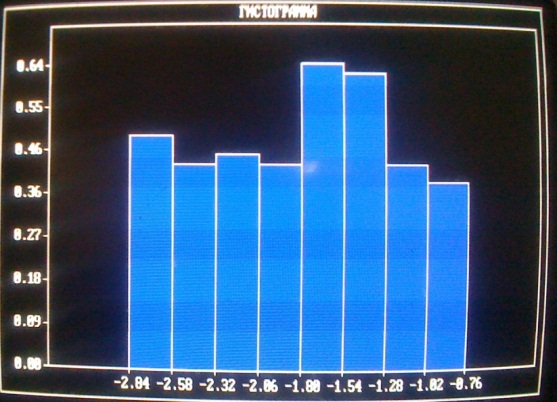
Таблица данных для построения гистограммы:
Интервал разбит [Xmin, Xmax] на 8 подинтервалов:
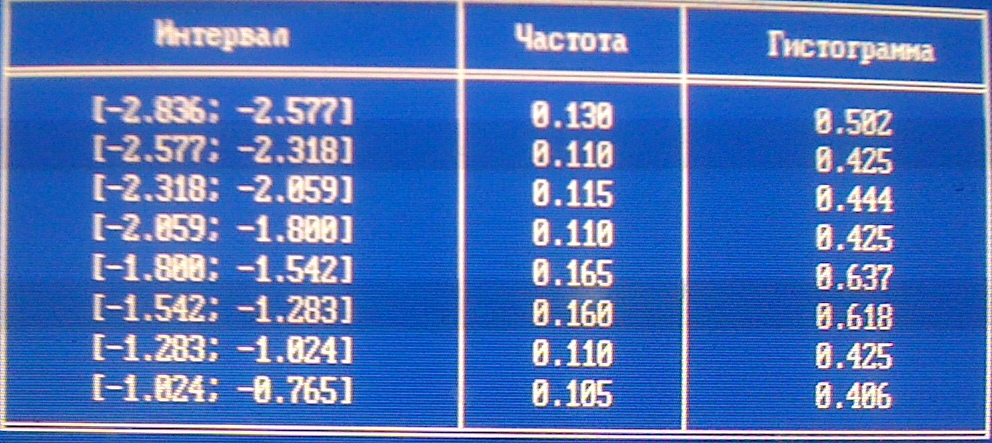
Для проверки предлагаются следущие гипотезы о законе распеределения случайной величины:
Гипотеза 1 нормальное распределение
Гипотеза 2 равномерное распределение
Гипотеза 3 экспоненциальное распределение
Введем номер наиболее правдоподобной гипотезы для ее проверки по критерики хи-квадрат Пирсона:
Гипотеза 1
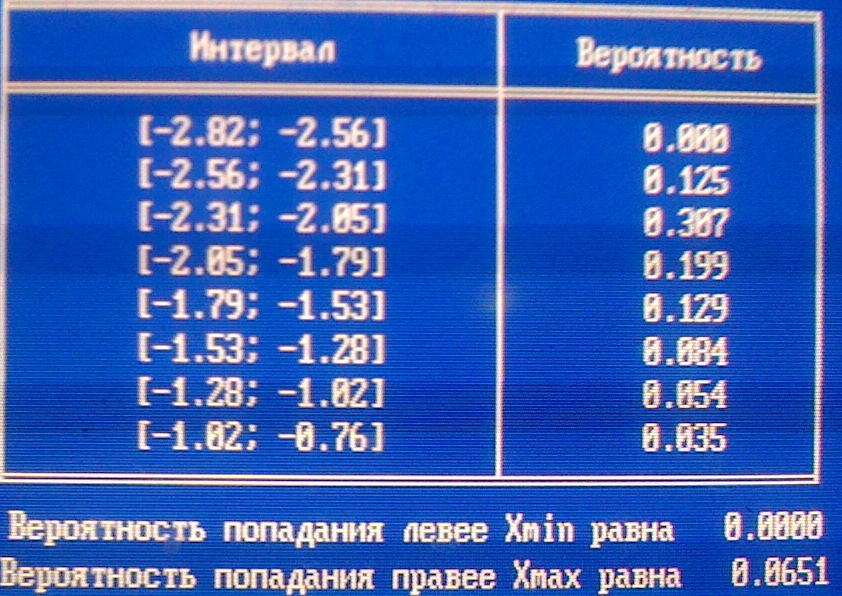
Таблица вероятностей попадания в интервал:
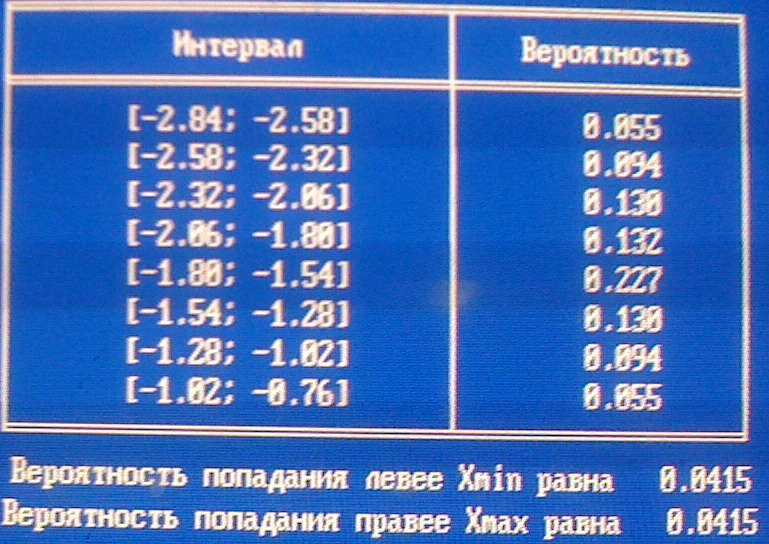
Значение статистики критерия Пирсона: g=69,972
Число степеней свободы равно 7
Нельзя ли принять проверяемую гипотезу на уровне 0.05?
r |
P |
|||||||||||||
0,99 |
0,98 |
0,95 |
0,90 |
0,80 |
0,70 |
0,50 |
0,30 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
0,001 |
|
7 |
1,239 |
1,564 |
2,17 |
2,83 |
3,82 |
4,67 |
6,35 |
8,38 |
9,80 |
12,02 |
14,07 |
16,62 |
18,48 |
24,30 |
Из таблицы распределения хи-квадрат Пирсона можно увидеть, что данную гипотезу нельзя принять ни на каком уровне, т.к. 69.972>24.30.
Проверяем гипотезу 2:
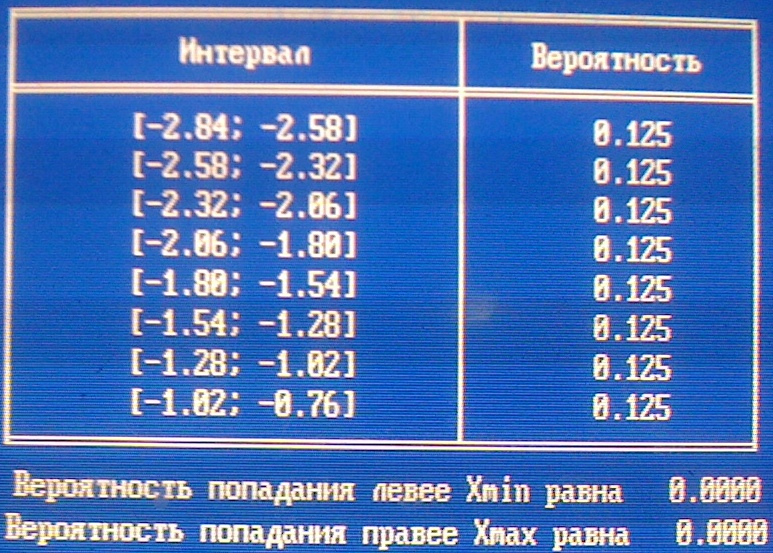
Значение статистики критерия Пирсона: g=6,448
Число степеней свободы равно 7
Нельзя ли принять проверяемую гипотезу на уровне 0.05?
r |
P |
|||||||||||||
0,99 |
0,98 |
0,95 |
0,90 |
0,80 |
0,70 |
0,50 |
0,30 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
0,001 |
|
7 |
1,239 |
1,564 |
2,17 |
2,83 |
3,82 |
4,67 |
6,35 |
8,38 |
9,80 |
12,02 |
14,07 |
16,62 |
18,48 |
24,30 |
Из таблицы распределения хи-квадрат Пирсона можно увидеть, что данную гипотезу нельзя принять на уровне значимости 0.05, но можно принять на уровне значимости 0.30, т.к. 6.35<6.448<8.38. Проверим остальные гипотезы.
Проверяем гипотезу 3:
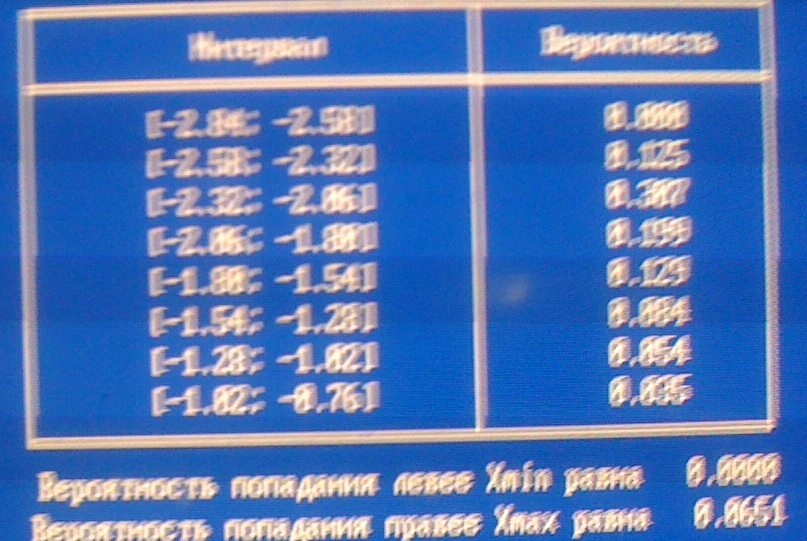
Значение статистики критерия Пирсона: g=200113,266
Число степеней свободы равно 7
Нельзя ли принять проверяемую гипотезу на уровне 0.05?
r |
P |
|||||||||||||
0,99 |
0,98 |
0,95 |
0,90 |
0,80 |
0,70 |
0,50 |
0,30 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
0,001 |
|
7 |
1,239 |
1,564 |
2,17 |
2,83 |
3,82 |
4,67 |
6,35 |
8,38 |
9,80 |
12,02 |
14,07 |
16,62 |
18,48 |
24,30 |
Из таблицы распределения хи-квадрат Пирсона можно увидеть, что данную гипотезу нельзя принять ни на каком уровне, т.к. 200113,266>24.30.
Проанализировав результаты значений статистики критерия Пирсона, можно принять гипотезу о том, что данное распределения является экспоненциальным.
Сделаем параметрическую оценку закона распределения для n=200.
Так как распределение является экспоненциальным, функция будет иметь вид:
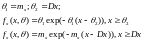
Оценка математического ожидания: -1,000
Оценка дисперсии: 0.357
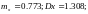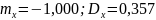то есть
то
есть:
