
- •2. Інтерполяція кубічними сплайнами.
- •3.) Інтерполяційні многочлени Лагранжа.
- •12). Локальне згладжування експериментальних даних.
- •13). Побудова формул для чисельного диференціювання х використанням інтерполяційних многочленів Ньютона.
- •14). Метод невизначених коефіцієнтів отримання формул для чисельного диференціювання.
- •15). Точність формул для чисельного диференціювання.
- •16). Метод Рунге-Ромберга покращення точності формул для апроксимації похідних.
- •17). Метод Ейткена покращення точності формул для апроксимації похідних.
- •21).Побудова квадратурних формул для чисельного інтегрування за допомогою методу невизначених коефіцієнтів.
21).Побудова квадратурних формул для чисельного інтегрування за допомогою методу невизначених коефіцієнтів.
. В залежності від того які ми накладаємо умови на величини і , можна побудувати різні типи квадратурних формул. Якщо ми накладаємо умову, що всі вузли є рівновіддаленими з кроком , а значення ваг шукатимемо з умови, що квадратурна формула була точною для алгебраїчних многочленів якомога вищої степені, то отримаємо формули Ньютона-Котеса.
Розглянемо випадок трьох вузлів .
Накладаємо
умову, то формула має бути точною для
многочленів
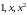 .
Отримаємо систему лінійних алгебраїчних
рівнянь для знаходження коефіцієнтів
:
.
Отримаємо систему лінійних алгебраїчних
рівнянь для знаходження коефіцієнтів
:
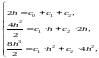

Знаходимо,
що
 ,
,
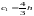 ,
,
 .
Ми вивели формулу Сімпсона.
.
Ми вивели формулу Сімпсона.
Відмітимо деякі загальні властивості квадратурних формул Ньютона-Котеса. Для коефіцієнтів справедливі наступні співвідношення
1. .
.
2.

3.
Коефіцієнтами
не є знаковизначеними при рості
,
що впливає на стійкість сумування при
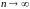 .
.
4.
Формули Ньютона - Котеса для
 вузла (
-парне),
що відповідає відрізку інтегрування
(
вузла (
-парне),
що відповідає відрізку інтегрування
(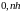 )
є точними для многочленів степені
.
Квадратурні формули, що відповідають
і
є точними для многочленів однакової
степені.
)
є точними для многочленів степені
.
Квадратурні формули, що відповідають
і
є точними для многочленів однакової
степені.
22). Точність квадратурних формул для чисельного інтегрування.
використаємо розклад функції в ряд Тейлора з залишковим членом в інтегральній формі.
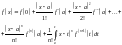
Також використаємо узагальнену теорему про середнє
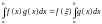 ,
де
,
де
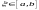
Оцінимо для прикладу точність формули Сімпсона.
 Якщо
функція
Якщо
функція
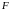 є первісною до функції
є первісною до функції
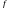 ,
то
,
то
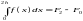
Знаходимо:
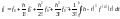
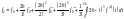 Отримаємо:
Отримаємо:
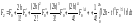 Врахуємо,
що
Врахуємо,
що
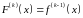
Знаходимо:

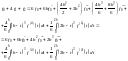
Точність квадратурної формули:

23). Складові квадратурні формули.
Розглянемо метод
побудови складової квадратурної формули
на прикладі складової формули Сімпсона.
Розіб’ємо відрізок інтегрування
 на
на
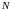 однакових відрізків (
однакових відрізків (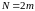 - парне). Довжина кожного відрізка
- парне). Довжина кожного відрізка
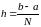 .
Врахувавши властивості означених
інтегралів, представимо вираз для
обчислення інтегралу у вигляді суми
.
Врахувавши властивості означених
інтегралів, представимо вираз для
обчислення інтегралу у вигляді суми
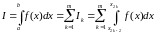 .
.
Для обчислення
кожного інтегралу
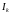 застосуємо квадратурну формулу
Сімпсона
застосуємо квадратурну формулу
Сімпсона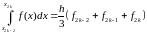 . Виконавши
сумування, отримаємо складову формулу
Сімпсона
. Виконавши
сумування, отримаємо складову формулу
Сімпсона
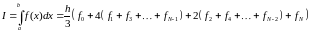 ,
,
де
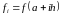 .
Отримаємо вираз оцінки точності
складової формули Сімпсона. Позначимо
залишковий член в квадратурній формулі
Сімпсона для обчислення інтегралу
як
.
Отримаємо вираз оцінки точності
складової формули Сімпсона. Позначимо
залишковий член в квадратурній формулі
Сімпсона для обчислення інтегралу
як
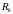 .
Очевидно, що залишковий член складової
формули Сімпсона можна записати як
.
Очевидно, що залишковий член складової
формули Сімпсона можна записати як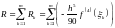
де
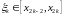 .
Використавши теорему про середнє,
отримаємо
.
Використавши теорему про середнє,
отримаємо

де
 .
Як бачимо складова формула Сімпсона
має 4 порядок точності.
.
Як бачимо складова формула Сімпсона
має 4 порядок точності.
24). Методи Рунге-Ромберга покращення точності квадратурних формул.
Точність кваадратурної
формули визначається залишковим членом,
який в загальному випадку можна записати
як
,
де
-порядок
квадратурної формули. Нехай
 - точне значення інтегралу, а
- точне значення інтегралу, а
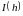 - наближене значення інтегралу обчислене
за допомогою деякої складової квадратурної
формули з кроком
.
В цьому випадку ми можемо записати:
- наближене значення інтегралу обчислене
за допомогою деякої складової квадратурної
формули з кроком
.
В цьому випадку ми можемо записати: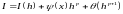 .
.
Обчислимо по цій
самій формулі наближене значення
інтегралу з кроком
: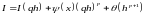 .Знайшовши
з цих двох рівнянь вираз для невідомого
залишкового члена, отримаємо уточнене
значення інтегралу, порядок точності
якого складає
.Знайшовши
з цих двох рівнянь вираз для невідомого
залишкового члена, отримаємо уточнене
значення інтегралу, порядок точності
якого складає
 :
: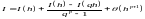
25). Методи Ейткена покращення точності квадратурних формул.
МетодЕйткенаприскореннязбіжності.
Припустимо,що
якийсьітераційнийметодмаєлінійнузбіжність,тобто:
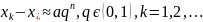
Числаa,
q,
x,
заздалегідь невідомі,алеїх
можназнайти,використовуючи
трипослідовніітерації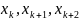 .
.
Складеморівняння:
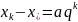 ,
,
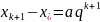 ,
,

(тутрівностітребарозумітияк наближені), з яких знайдемо
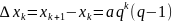 ,
,
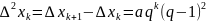 ,
,
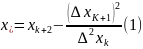
Метод Ейткенаприскореннязбіжностіполягаєв тому,щопісля обчислення проводитьсяперерахунокза формулою
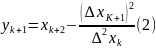
і
значення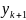 ,приймаєтьсязанове
наближення.
Якбирівність
(1)виконувалосяточно,то
співпалоб
зточнимзначеннямх.Узагальному випадку
дає
кращенаближення до
,приймаєтьсязанове
наближення.
Якбирівність
(1)виконувалосяточно,то
співпалоб
зточнимзначеннямх.Узагальному випадку
дає
кращенаближення до ,
ніж черговаітерація
,
ніж черговаітерація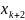 .Підкреслимо,що
головнимприпущеннямтутє
вимогалінійноїзбіжностіосновногоітераційногометоду.У
випадкуметодів,
що мають більш високушвидкістьзбіжності
(наприклад
методуНьютона),
прискорення поЕйткенув
формі (2) є
неефективним.
.Підкреслимо,що
головнимприпущеннямтутє
вимогалінійноїзбіжностіосновногоітераційногометоду.У
випадкуметодів,
що мають більш високушвидкістьзбіжності
(наприклад
методуНьютона),
прискорення поЕйткенув
формі (2) є
неефективним.
На практиці не обов'язково проводити перерахунок за формулою (2) на кожній ітерації k. Натомість вживають методи, в яких та-такий перерахунок здійснюється циклічно, тобто через певне число основних ітерацій. За допомогою методу Ейткена на основі відомих ітераційних методів можна отримати іноді нові ітераційні методи, яким властива висока збіжність.
