Катушка индуктивности с ферромагнитным сердечником.

Цель работы: изучение зависимости параметров катушки с ферромагнитным сердечником от приложенного к ее обмотке напряжения.

В результате выполнения работы каждый студент должен усвоить основные характеристики катушки с ферромагнитным сердечником как нелинейного элемента электрических цепей; понимать физические процессы, обуславливающие нелинейность параметров катушки; уметь опытным путем определять характеристики катушки и представлять эти характеристики в виде таблиц и графиков.

Краткие теоретические и практические сведения.

Изучение свойств катушки с ферромагнитным сердечником представляет в практической электротехнике особый интерес, так как такая катушка является упрощенной моделью многих элементов электрических машин и аппаратов (катушек электроизмерительных приборов, трансформатора, работающего в режиме холостого хода, реле, контакторов и т.д.)

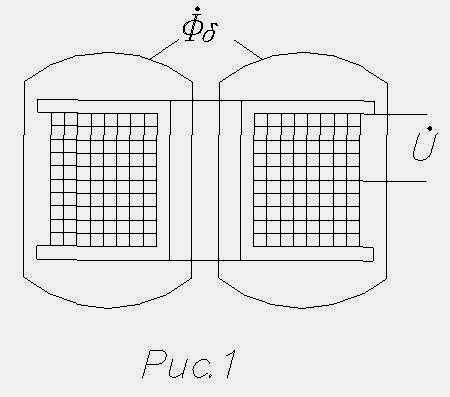На рис.1 изображена катушка, намотанная на каркас, который выполнен из немагнитного материала, магнитная проницаемость (µ_а) которого и окружающего пространства практически равна магнитной проницаемости воздуха: µ₀=4π·10^-7 Гн/м. Поэтому при протекании по катушке синусоидального тока магнитный поток будет также синусоидальным, совпадающим по фазе с током.

Если катушку индуктивности разместить на замкнутом сердечнике (рис.2), выполненном из электротехнической стали и питать ее от источника переменного тока, то магнитодвижущая сила (МДС) катушки i₁w₁ будет возбуждать основной магнитный поток Ф₁ и поток рассеяния Ф_σ. При переменном напряжении U₁, подводимом к катушке, ток i₁, МДС i₁w₁, а также потоки Ф₁ и Ф_σ периодически изменяются по величине и направлению. Магнитным потоком Ф₁ в катушке индуктируется ЭДС самоиндукции е₁, потоком Ф_σ – ЭДС рассеяния е_σ .

На основании второго закона Кирхгофа, при указанных на рис.3 условных положительных направлениях, можно записать

(1)

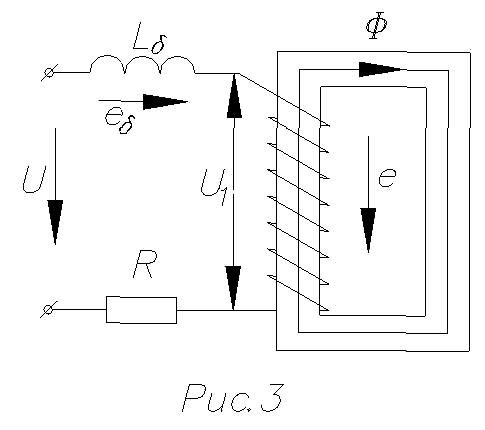Как видно, напряжение u₁, подводимое к катушке, уравновешивается тремя составляющими: ЭДС самоиндукции е₁ и рассеяния е_σ, падением напряжения на активном сопротивлении R катушки индуктивности.

Уравнение, характеризующее электрическое состояние катушки с ферромагнитным сердечником, показывает, что ток зависит не только от приложенного напряжения и сопротивления R обмотки, но также и от характеристик магнитной цепи, влияющих на потокосцепление Ψ₁=w₁Ф₁ и Ψ_σ=L_σ·i₁, которые в свою очередь, влияют на ЭДС е₁ и е_σ.

В линейных цепях (рис.1) ЭДС e₁ заменяется падением напряжения на индуктивности, которое равно по величине и противоположно по фазе ЭДС е₁. Аналогичную операцию можно проделать с ЭДС поля рассеяния е_σ, так как практически она является результатом воздействия поля в немагнитной среде (магнитный поток Ф_σ замыкается по воздуху):

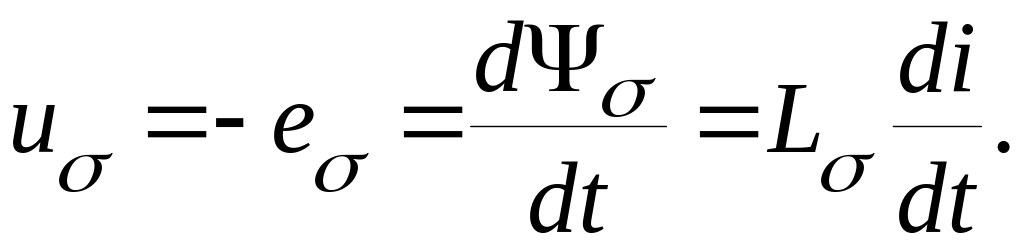
Индуктивность рассеяния L_σ является постоянной величиной вследствие линейной зависимости потоков рассеяния от тока: Поэтому уравнение (1) можно переписать следующим образом:

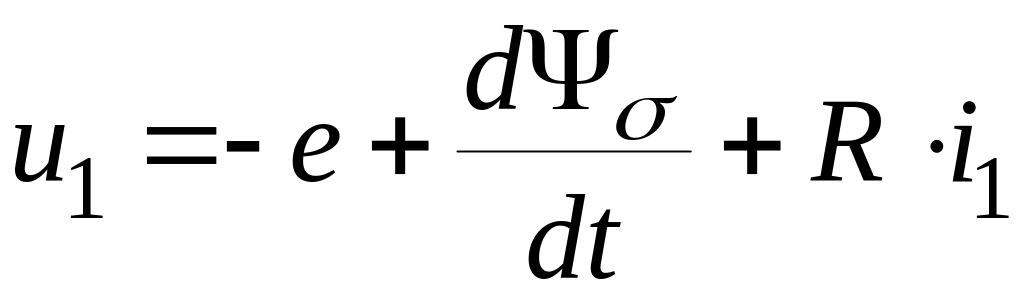(2)

Уравнение (2) позволяет предположить, что реальная катушка индуктивности с ферромагнитным сердечником как бы состоит из двух последовательно соединенных катушек (рис.3). Первая из них является линейной катушкой с активным сопротивлением R и индуктивностью L_σ, а вторая – идеализированной катушкой с числом витков w, активное сопротивление которой равно нулю. Поток этой катушки замыкается только по сердечнику, напряжение на ней u^´₁= -e₁.

Отличительной особенностью идеализированной катушки с ферромагнитным сердечником по сравнению с катушкой, помещенной в не магнитную среду является то, что для нее нельзя найти линейную связь между напряжением u₁ и проходящим по катушке током i₁ аналогичную 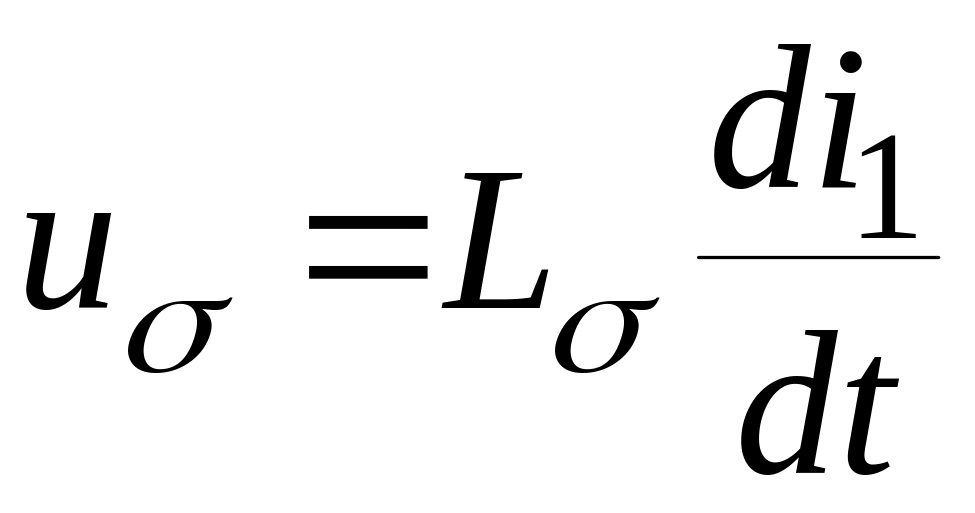, поскольку магнитный поток и намагничивающий ток катушки с ферромагнитным сердечником связаны между собой нелинейной характеристикой , т.е. такую катушку нельзя характеризовать постоянной индуктивностью. Поэтому при анализе электрических цепей переменного тока, содержащих катушку индуктивности с ферромагнитным сердечником, вводятся предпосылки, упрощающие реальный физический процесс, протекающий в катушке.