Двійкова система числення

В аналоговій техніці існує ряд властивих їй недоліків: інформаційні спотворення при передачі, які не підлягаючі виправленню, складність запам’ятовування і невисока точність. Ці недоліки примусили звернутися до нової форми представлення інформації – цифровий.

У цифровій техніці безперервні повідомлення, інформація представляється в дискретній формі. Кожне значення дискретного сигналу можна представити числом. У цифровій техніці такий процес називається кодуванням, а сукупність одержаних чисел – кодом сигналу. Таким чином, дискретне повідомлення складається з набору чисел і символів (наприклад, знаків «+» «–»). Кожне слово складається з цифр. Спосіб запису чисел цифровими знаками називається системою числення. У цифровій техніці використовуються так звані позиційні системи числення. Значення кожної цифри, що входить у склад числа, залежить від її положення у записаному числі. Кількість різних цифр, що вживаються у позиційній системі, називають основою системи. У цифровій техніці найбільшого поширення набула двійкова система числення, що містить тільки цифри 0 і 1, а її основою служить число 2. Наприклад, число 25 в десятковій і двійковій системах може бути представлено у вигляді:

25₁₀ = 2·10¹ + 5·10⁰ = 1·2⁴ + 1·2³ + 0·2² + 0·2¹ + 1·2⁰.

Іноді використовують вісімкову і шістнадцяткову системи. Їх, зокрема, застосовують при складанні програм для зручнішого і коротшого запису двійкових кодів команд, оскільки ці системи не вимагають спеціальних операцій для перекладу в двійкову систему.

Числа десяткової системи числення неважко перевести у числа двійкової системи. Щоб перевести ціле число з основою 10 в систему з основою 2, необхідно послідовно ділити задане число на 2 і число, що було одержано в процесі поділу – частка, знов ділиться на 2 до тих пір, поки остання частка не виявиться менше 2. Результат переводу записують у вигляді послідовності цифр зліва направо, починаючи з останньої частки і кінчаючи першим залишком (при цьому цифра молодшого розряду є перший залишок). Всі дії в процесі ділення числа виконують в десятковій системі.

Перехід від двійкового запису до десяткового виконується порозрядним підсумовуванням.

Правила виконання арифметичних дій над двійковими числами задаються табл. 5.

Таблиця 5

Двійкове складання	Двійкове віднімання	Двійкове множення
0 + 0 = 0	0 – 0 = 0	0 · 0 = 0
0 + 1 = 1	1 – 0 = 1	0 · 1 = 0
1 + 0 = 1	1 – 1 = 0	1 · 0 = 0
1 + 1 = 10	10 – 1 = 1	1 · 1 = 1

Логічні елементи

Всі математичні і логічні перетворення, які відбуваються з інформацією, здійснюються електронними першоцеглинками – логічними елементами.

Логічний елемент – це електрична схема, електронний пристрій, що реалізує одну з логічних функцій. На принциповій схемі логічний елемент зображають прямокутником, всередині якого відповідним значком вказується функція, яку він здійснює. Лінії з лівого боку прямокутника показують входи, а з правого – виходи елементу.

Основних логічних елементів, використовуваних в пристроях, три:

– елемент «АБО»,

– елемент «І»,

– елемент «НЕ»,

Елемент «АБО» (диз’юнктор)

Елемент «АБО» виконує операцію логічного складання:

У = X1 + X2.

Н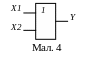 а мал. 4 показане умовне графічне позначення диз’юнктора. Число входів Х у нього може бути два і більше. Сигнали «0» і «1» (низького і високого рівня різко відрізняються за значенням напруги і не можуть бути сплутані між собою. Для мікросхем ТТЛ серій сигнал «1» повинен мати напругу U ¹ = 2,4 … 5 В, а сигнал «0» – U ⁰ = 0 … 0,4 В. Для мікросхем КМОП-структур:

U ¹ = 0,7U _живл ;

U ⁰ = 0,3U _живл.

Сигнал «1» з’явиться на виході Y, якщо на будь-якому одному або декількох входах присутній «1»; сигнал «0» – тільки у тому випадку, коли на всі входи X поступає сигнал «0».

Елемент «І» (кон’юнктор)

Елемент «І» виконує операцію логічного множення:

Y = X1 · X2.

К ількість входів X може бути будь-яким (від двох і більш). У цьому елементі на виході Y з’являється логічна «1» тільки у тому випадку, коли на всі входи X подається сигнал «1». За наявності логічного «0» хоча б на одному з входів на виході буде сигнал «0».

Умовне графічне позначення кон’юнктора виконане на мал. 5.

Елемент «НЕ» (інвертор)

Елемент не виконує операцію логічного заперечення:

.

В ін має лише один вхід. Сигнал «1» на виході Y з’явиться у разі, коли на вхід Х поступає сигнал «0»; коли ж на вхід Х поступає «1», з виходу Y знімається сигнал «0».

На мал. 6 показане умовне графічне позначення інвертування.

На початку були розглянуті електричні схеми, що виконують логічні операції, на електромагнітних реле. Ці ж функції виконують логічні елементи. Наведемо приклади реалізації логічних схем на електронних елементах (мал. 7).

В икористовуючи ці три основні логічні елементи, можна побудувати безліч логічних пристроїв, що виконують будь-які складні перетворення. Ці перетворення є комбінаціями простих логічних операцій. Розглянемо лише два з них, які є універсальними, оскільки, маючи тільки ці елементи, можна побудувати будь-який логічний пристрій. Це елементи «І-НЕ» і «АБО-НЕ».