Логічне множення (кон’юнкція)

При логічному множенні вхідні змінні (число співмножників може бути будь-яким) з’єднуються сполучником «І» і позначають символом «  » або знаком множення (·) і записується вона у вигляді:

Y = Х1  Х2

або:

Y = Х1·Х2.

Запис читається таким чином: Y дорівнює XI І Х2. Така функція Y = Х1·Х2

Х1	Х2	Y = Х1·Х2
0	0	0
1	0	0
0	1	0
1	1	1

Таблиця 2

приймає значення логічної «1» тільки при рівності одиниці всіх вхідних змінних (Х1=Х2 = 1). Якщо хоч одна змінна буде рівна 0, то і вихідна функція теж буде рівна нулю. Таблиця істинності для кон’юнкції має вигляд:

Р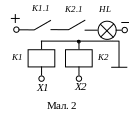 озглянемо електричну схему, що виконує операцію логічного множення. Схема побудована на електромагнітних реле, контакти яких включені, на відміну від схеми, приведеної на мал. 1, не паралельно, а послідовно. Лампочка HL в колі сигналу Y зажевріє тільки тоді, коли всі контакти (К1 і К1) будуть замкнуті, тобто при одночасному спрацьовуванні всіх реле (Х1=1 і Х2 = 1) (мал. 2).

Логічне заперечення (інверсія)

При логічному запереченні (функція «НЕ») значення вихідної функції протилежне вхідній змінній. Операція записується у вигляді:

і читається: Y дорівнює не Х. Це значить, що Y істинно, якщо Х хибне (Х = 0) і навпаки.

Таблиця 3

Х	Y
0	1
1	0

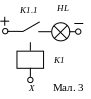О перація логічного заперечення може бути реалізована на одному електромагнітному реле (мал. 3), що має нормально замкнуті контакти (контакти на розмикання), тобто за відсутності сигналу Х (Х =0) коло замкнуто, про що свідчитиме лампочка, що світиться, але коли на вхід X буде поданий сигнал (Х =1) – коло розімкнеться і лампочка потухне.

Схемна реалізація різних функцій дозволяє створювати різні функціональні елементи, на яких побудована сучасна електронно-обчислювальна техніка.

При схемній реалізації ставиться вимога – задіювати якомога менше число елементів, що входять в схему. Щоб це здійснити, треба:

1. перекласти задачу, поставлену перед конструктором, на мову алгебри логіки (задача представляється у вигляді складного вислову, функції перемикача, що описує той або інший функціональний вузол);

2. мінімізувати даний складний вислів, тобто провести тотожні перетворення, які дозволять спростити запис функції перемикача, а, отже, і практично її реалізувати;

3. за спрощеним записом виробити схемну реалізацію поставленої задачі.

При мінімізації логічних функцій використовують наступну основну тотожність і закони алгебри логіки.

Все це властивості операцій « + » і « · »:

Таблиця 4

для диз’юнкції		для кон’юнкції
Х + Х = Х		Х · Х = Х
Х + 1 = 1		Х · 1 = Х
Х + Х = Х		Х · 0 = 0
	= Х

Пересувний закон:

Х1 + Х2 = Х2 + Х1; Х1 · Х2 = Х2 · Х1.

Сполучний закон:

(Х1 + Х2) + Х3 = Х1 + (Х2 + Х3); (Х1 · Х2) · Х3 = Х1 · (Х2 · Х3).

Розподільний закон:

– операції «+» відносно « · »:

Х · (Y + Z) = Х · Y + Х · Z;

– операції « · » відносно « + »:

Х + (Y · Z) = (Х + Y) · (Х + Z);

У останньої формули не зовсім звичний вигляд, але користуюся вказаною вище вказаною тотожністю, можна довести справедливість цієї рівності і сформулювати наступне правило: щоб виконати операцію з комплексом, треба виконати її з кожним учасником комплексу і результати об’єднати операцією комплексу.

Для мінімізації логічних функцій перемикачів користуються ще такими формулами:

– формула поглинання: X + X · Y = X,

– формула склеювання: X · Y + X ·· = X.

Важливе значення при тотожних перетвореннях має співвідношення подвійності (теореми де Моргана):

,

.

Це допомагають взаємно замінювати операції диз’юнкції і кон’юнкції, а це дає можливість побудувати будь-яку логічну функцію, використовуючи тільки дві операції «І» та «НЕ» або «АБО» і «НЕ».

Перевірити справедливість всіх виразів можна за допомогою таблиць істинності.