4. Предложение «Некоторый s не есть р» истинно тогда и только тогда, когда классы s и р находятся в одном из следующих отношений:
№ 1 № 2
S Р
№ 3 № 4
S Р
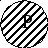
№ 5
№ 5
П
римерами
соответствующих высказываний для каждой
модельной схемы будут высказывания:1)
«Некоторое натуральное число, меньшее
100, не является натуральным числом,
большим 80», 2) «Некоторый учащийся не
является спортсменом», 3) «Некоторый
юридически ненаказуемый поступок не
есть преступление», 4) «Некоторое
натуральное число не является
иррациональным», 5) «Некоторый писатель
не является поэтом».
5. Предложение «а есть р» истинно тогда и только тогда, когда между предметом, обозначенным термином «а», и классом р существует отношение, соответствующее схеме №1:
Это значит, что предмет а является элементом класса Р. Например: «Д.И.Менделеев – химик», «2 – четное число», «Лондон – город» и т.д.
6. Предложение «а не есть р» истинно тогда и только тогда, когда между предметом, обозначенным термином «а», и классом р существует отношение, соответствующее схеме №2:
№ 1 № 2
а
Это значит, что предмет а не является элементом класса Р. Например: «5 не является четным числом», «Наполеон не является англичанином» и др.
Распределенность терминов в суждениях
В модельных схемах мы штрихуем те классы, которые являются «объемом сказывания», то есть те множества предметов из класса S, для которых предицируемое в соответствующих предложениях наличие или отсутствие свойства Р оказывается выполненным.
Понятие распределенности терминов – очень важное семантическое понятие – его можно ввести через эту штриховку.
Термин, входящий в состав категорического атрибутивного высказывания, распределен в нем, если и только если в каждой модельной схеме, которая является условием истинности высказываний этого типа, класс предметов, обозначенный данным термином, полностью заштрихован или полностью не заштрихован. В противном случае будем говорить, что термин нераспределен.
Теперь мы можем рассмотреть модельные схемы для высказываний типа а, е, i, о. Распределенные термины обозначаются знаком «+», а нераспределенные термины – «–». Соответственно получаем следующий список:
Всякий S+ есть Р–.
Всякий S+ не есть Р+.
Некоторый S– есть Р–.
Некоторый S– не есть Р+.
а+ есть Р–
а+ не есть Р+
Термины единичных высказываний распределены точно так же, как они распределены в соответствующих общих высказываниях. Это и позволяет считать, что высказывания единичноутвердительные – аналоги общеутвердительных, а единичноотрицательные – аналоги общеотрицательных. Поэтому единичные утверждения не играют самостоятельной роли и всегда трактуются как высказывания общие.
Сложные суждения и их логическая структура
Сложные суждения – это суждения, которые содержат в качестве своей правильной части некоторое (по крайней мере одно) другое суждение.
Отношения между суждениями. Различают отношения логические и фактические. Для каждого вида логического отношения есть некоторый аналог фактического отношения. Первые зависят от логических форм высказываний, вторые – от их конкретных содержаний.
Высказывания А и В находятся в отношении контрарной противоположности, если и только если В эквивалентно отрицанию С. Высказывания А и В контрарно противоположны, если и только если никакие высказывания, которые имеют те же логические формы, что А и В, не могут быть вместе истинными, но могут быть вместе ложными. Таковы, например, высказывания вида «Все S есть Р» и «Ни одно S не есть Р». Очевидно, что здесь «Ни одно S не есть Р» эквивалентно отрицанию «Некоторые S есть Р».
Суждение вида «Все S есть Р» и «Ни одно S не есть Р» не могут быть оба истинными, но могут быть оба ложными. Отличие контрарной противоположности от контрадикторной состоит в том, что контрадикторно противоположные суждения не могут быть не только оба истинными, но и оба ложными. Для контрарных же суждений возможность ложности обоих не исключена.
Отношения совместимости/несовместимости высказываний по истинности, а также совместимости их по ложности.
Совместимы по истинности такие высказывания А и В, которые могут быть оба истинными.
Высказывания А и В совместимы по ложности, если и только если они могут быть оба ложными.
Отношения логического следования и эквивалентности – это виды отношения совместимости по истинности, а контрарная и контрадикторная противоположности – виды отношения несовместимости по истинности.