2.2.2. Матрицы переходов, выходов

Матрицы в отличие от таблиц характеризуются однородностью обозна -чений строк и столбцов. Строки матриц соответствуют предыдущим состоя-

ниям (ПС), а столбцы - данным состояниям (ДС).

Р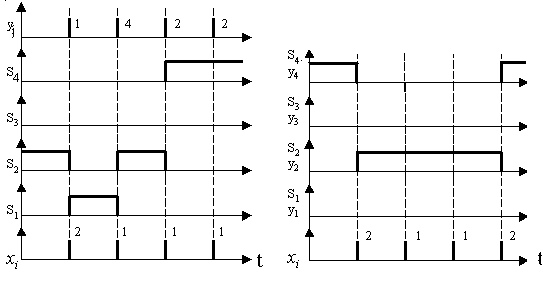ис.13. Диаграммы работы ЦА Мили Рис.14. Диаграммы работы ЦА Мура

Матрицы переходов (МП) для обоих автоматов аналогичны, применительно к рассматриваемым примерам они должны иметь по 4 строки и по 4 столбца. На пересечениях МП размещаются входные сигналы.

Табл.10 является МП ЦА Мили , а табл.11 - МП ЦА Мура. Видно, что имеются пустые пересечения. В строке не могут использоваться одинаковые элементы. Этого ограничения нет для столбцов.

Очевидно, что чистой МВ для автоматов не получится, так как без входных сигналов x_i матрица теряет смысл. Поэтому МВ на рис.9 зачеркнута.

Если в матрицах переходов автоматов Мили и Мура на пересечениях разместить и выходные сигналы (x_i / y_j и x_i / y_t), то получатся совмещенные матрицы переходов и выходов (СМП и В).

Такая матрица для ЦА Мили показана в табл.12. В ней по отношению к выходным сигналам никаких ограничений нет.

СМП и В для ЦА Мура представлена табл.13. Естественно, что в ней имеется ограничение на выходные сигналы: индексы у выходных сигналов в столбце являются одинаковыми, они совпадают с индексом данного состояния, соответствующему рассматриваемому столбцу.

Так фиксировать выходные сигналы не только нецелесообразно, но даже и некрасиво. С учетом этого СМП и В для ЦА Мура на рис.9 обведена пунктирно.

Поэтому для ЦА Мура целесообразна отмеченная матрица переходов (ОМП). Переходы в такой матрице фиксируются на пересечениях, а выходные сигналы - под обозначениями данных состояний в верхней части матрицы (табл.14).

Условия корректности отмеченной матрицы переходов по отношению к входным сигналам совпадают с условиями корректности СМП и В ЦА Мили.

Таблица 10

МП ЦА Мили

ДС ПС	s1	s2	s3	s4
s1		x1	x2
s2	x2			x1
s3		x1	x2
s4	x2			x1

Таблица 11

МП ЦА Мура

ДС ПС	s1	s2	s3	s4
S1		x2	x1
s2		x1		x2
s3	x1		x2
s4	x1	x2

2.2.3. Графы автоматов

Граф ЦА (ГА) - ориентированный граф, у которого в качестве вершин используются состояния, а в качестве дуг - переходы. В начале дуги фиксируется входной сигнал. Что касается выходного сигнала, то он для ЦА Мили ставится на конце дуги (рис.15), а для ЦА Мура внутри вершины (рис.16).

Таблица 12

СТП и В ЦА Мили

ДС ПС	s1	s2	s3	s4
s1		x1 y4	x2 y3
s2	x2 y1			x1 y2
s3		x1 y4	x2 y3
s4	x2 y1			x1 y2

Таблица 13

СТП и В ЦА Мура

ДС ПС	s1	s2	s3	s4
s1		x2 y2	x1 y3
s2		x1 y2		x2 y4
s3	x1 y1		x2 y2
s4	x1 y1	x2 y2

Таблица 14

ОМП

ДС ПС	s1 y1	s2 y2	s3 y3	s4 y4
s1		х2	х1
s2		х1		х2
s3	х1		х2
s4	х1	х2

Рис.15. ГА Мили Рис.16. ГА Мура

Условия корректности для ГА Мили можно сформулировать следующим образом:

1) при выходе из данного состояния должны использоваться разные входные сигналы;

2) при заходе в данные состояния допускаются одинаковые входные сигналы;

3) при заходе в данное состояние разрешаются одинаковые выходные сигналы.

Условия корректности для ГА Мура являются не сколько другими:

1) при выходе из данного состояния должны использоваться разные входные сигналы;

2) при заходе в данные состояния могут использоваться одинаковые входные сигналы;

3) при заходе в данное состояние должны быть одинаковые выходные сигналы.

Можно заметить, что если в ЦА Мили при заходе в каждое состояние имеются одинаковые выходные сигналы, то такой ЦА можно легко преобразовать в автомат Мура. Что касается преобразования автомата Мура в автомат Мили, то для этого достаточно перенести выходные сигналы из вершин на концы дуг.