Доказательство:

В правой части стоит сумма из n(n-1)!=n! произведений различных элементов матрицы A, причем, в силу леммы, они входят с тем знаком, с каким они входят в detA.

В правой части не может быть одинаковых слагаемых, т.к. например, все слагаемые, содержащие a_i1, могут быть только в a_i1A_i1. Внутри суммы a_i1A_i1 тоже не может быть повторов. => Левая и правая части состоят из n! одних и тех же слагаемых без пропусков и повторений => (_*) справедливо:

Определитель произведения двух матриц равен произведению их определителей

Билет 13 – обратная матрица:

Обра́тная ма́трица — такая матрица A^-1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

Обратная матрица существует тогда и только тогда когда матрица А невыродженная

Необходимость.

Пусть существует А^(-1) тогда А невыродженная.

Если есть А^(-1) то det(A*A^(-1))=det A*det A^(-1)=1

Det A не равен 0

Достаточность.

Пусть det A не равен 0 то есть A^(-1)

Рассмотрим В=1/det A[A11 A21…An1] 1/det A[A11……A1n](T)

[A12 A22…An2]= [A21……A2n]

[A1n A21n..Ann] [An1……Ann]

докажем что В является левой обратной к А.

вычислим А*В

1/det A[A11 A21….An1] [a11 a1j a1n]

[A1i A2i…...Ani] [a21 a2j a2n]=C

[A1n A21n..Ann] [an1 anj ann]

Cij=1/detA(A1i*a1j+…+Ani*anj)=1/det A*det A*δij(1,i=g|0,i≠g) следовательно С=E

B есть левая обратная к А, аналогично что В является правой обратной к А.

A^(-1)=(1/det A)*(A(v))(T)

A(v)-союзная матрица из алгебраических дополнений.

Если матрица невырожденная, то существует и притом единственная матрица а-1.

14 Правило крамера решения СЛАУ.

Система линейных уравнений:

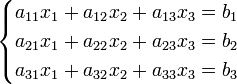
Определители:

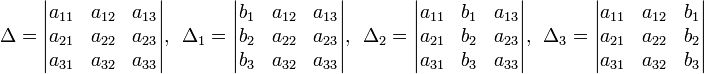
Решение:

Пример:

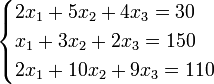
Определители:

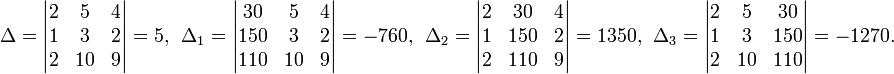
15. Линейная зависимость системы столбцов)строк) матрицы. Критерий линейной зависимости

Пусть матрица A=||a_ij|| (mxn)

Обозначим B₁,B₂,..,B_k – столбцы матрицы A

Определение: Столбцы B₁,..,B_k называются линейно зависимыми, если существуют числа , такие, что

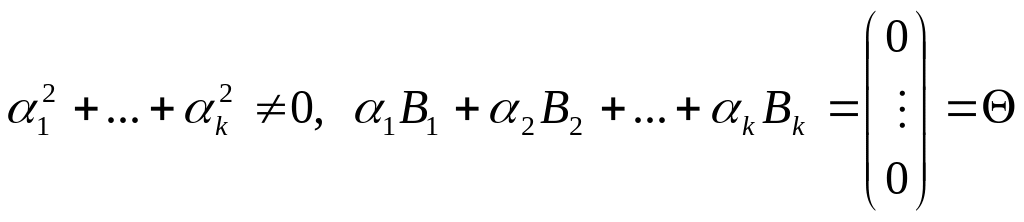
Определение: Столбцы B₁,…,B_k называются линейно независмыми, если равенство выполняется тогда и только тогда, когда α₁=α₂=α_k=0.

Утверждение: Столбцы B₁,…,B_k линейно зависимы тогда и только тогда, когда хотя бы один из них является линейной комбинацией других столбцов. Т.е. например, B₁=α₂B₂+…+α_kB_k.

16. Ранг матрицы. Теорема о базисном миноре.

Определение: Ранг матрицы A – максимальный порядок неравного нулю минора.

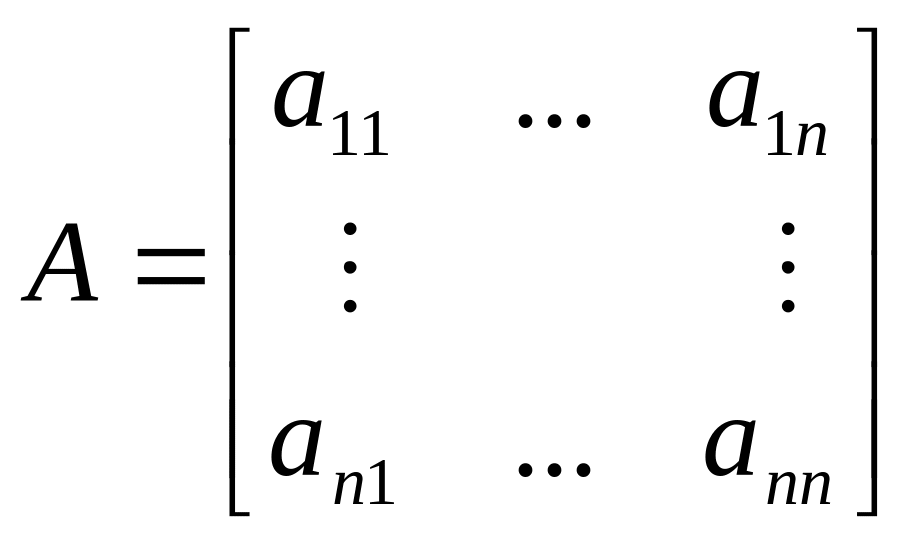Обозначается: RangA, r(A).

Определение: Минор, определяющий ранг матрицы, называется базисным. Строки и столбцы, формирующий базисный минор, называются базисными строками и столбцами.

Теорема (о базисном миноре): Базисные строки (столбцы) линейно независимы. Остальные строки (столбцы) являются линейными комбинациями базисных строк (столбцов).   Теорема. В произвольной матрице А каждый столбец (строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.Таким образом, ранг произвольной матрицы А равен максимальному числу линейно независимых строк (столбцов) в матриц

еДоказательство: Для столбца B

Пусть для определенности базисный минор (минор порядка r(≠0)) расположен в верхнем левом углу. Этот минор равен D≠0; все миноры порядка выше r равны нулю.

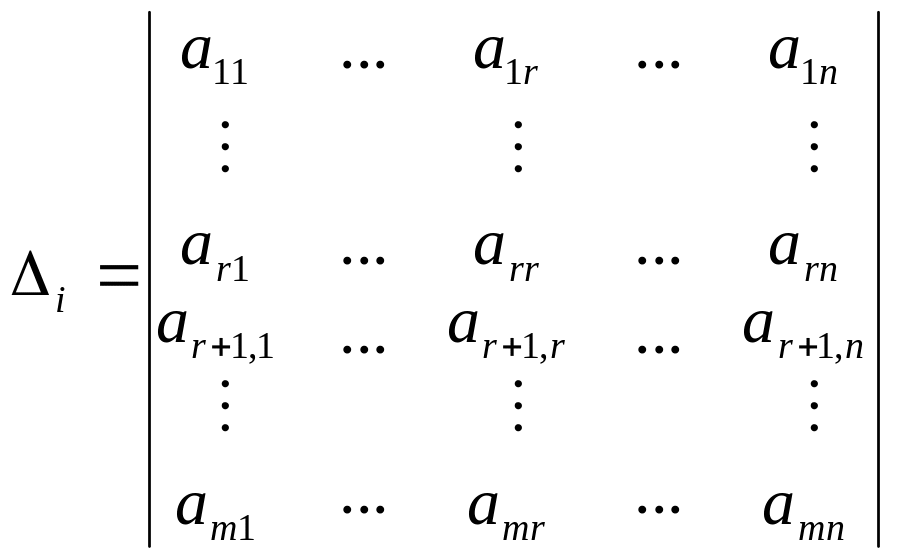
Предположим, что базисные столбцы линейно зависимы. Тогда бы базисный минор состоял из столбцов, один из которых является линейной комбинацией остальных столбцов в D (см. утверждение). Тогда в силу свойств определителя D=0 – пришли к противоречию => базисные столбцы линейно независимы. Докажем, что другие столбцы есть линейная комбинация базисных столбцов. Докажем это для l-того столбца . Рассмотрим вспомогательные определители порядка (r+1) вида:

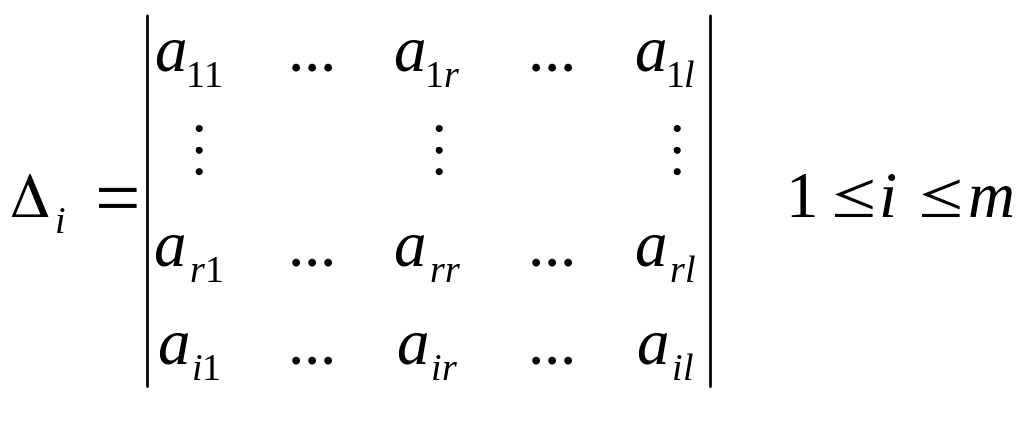
для т.к. две одинаковые строки

для т.к. в этом случае есть минор (r+1) порядка у матрицы A rangk<n

Выпишем разложение определителей по i-той строке:

Алгебраические дополнения A₁,…,A_r не зависят от индекса:

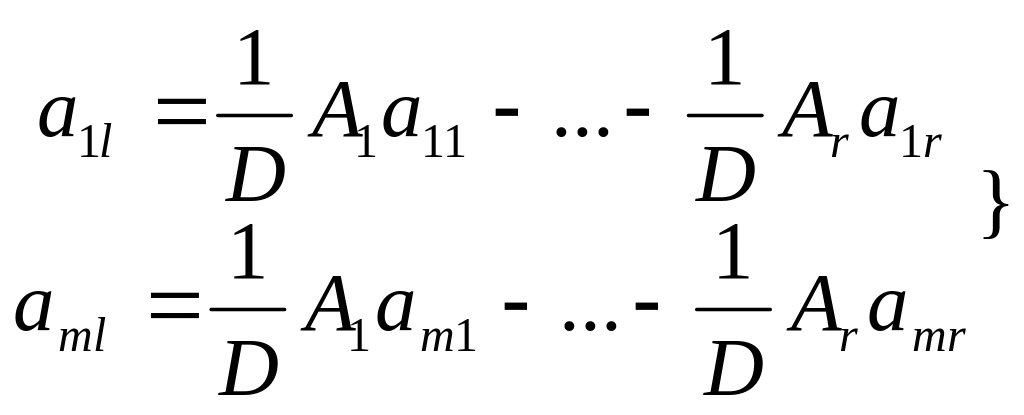m равно B

=> l-тый (l>r) есть линейная комбинация базисных столбцов B₁,…,B_r с коэффициентами

17.Следствие из теоремы о базисном миноре: о линейной зависимости системы строк определителя, равного нулю: аналогичный результат для столбцов

Если A — квадратная матрица, и det A = 0 <=> строки и столбцы этой матрицы линейно зависимы.

18. Следствие из теоремы о заданном миноре: О линейной зависимости системы из (n+1) строки длинною из n элементов

Ответ:

Ранг матрицы равен максимальному числу линейно независимых строк (столбцов) матрицы, т.е. если r — ранг матрицы, то в матрице есть r линейно независимых строк (столбцов), а любые r+1 строк (столбцов) — линейно зависимы.

19.Следствие ищ теоремы о базисном миноре: критерий линейной зависимости системы из m строк или столбцов

Ответ: Пусть r = rang A, тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно r.

20. Понятие ранга системы столбцов(строк) матрицы. Теорема о ранге матрицы

Определение: Ранг матрицы A – максимальный порядок неравного нулю минора.

Обозначается: RangA, r(A).

Ответ: Теорема (о ранге матрицы): Ранг матрицы равен максимальному числу линейно независимых строк (столбцов).

Доказательство: Докажем для столбцов. Пусть RangA=r. Надо доказать, что r=k, где k – максимальное число независимых столбцов любого множеств, состоящего из больше, чем k столбцов.

Предположим, что k<r. Это невозможно, т.к. существует к линейно независимых базисных столбцов. Следовательно R≥r.

Предположим, что k>r. Докажем, что это невозможно.

Пусть столбцы C₁,…,C_k – линейно независимы. Обозначим B₁,…,B_k – базисные столбцы (может быть, некоторые из столбцов C совпадают с столбцами B). Каждый из столбцов C₁,…,C_k может быть записан в виде линейной комбинации базисных столбцов:

Составим некоторую линейную комбинацию из столбцов. Тогда достаточно будет выражения равенства:

матричное равенство. m уравнений в правой части – 0, относительно k неизвестных β₁,…,β_k, k>m

При рассмотрении метода Гаусса докажем, что ненулевое решение такой системы. Т.е.

не все равны нулю: . Но это противоречит предположению о линейной независимости столбцов C₁,…,C_k

Вывод: k<r – невозможно, k>r – невозможно, следовательно, k=r.

21

Элементарными преобразованиями матрицы называют следующие:

1. Перестановка строк (столбцов).

2. Умножение строки (столбца) на число, отличное от нуля.

3. Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.

4. Вычёркивание строки (столбца), все элементы которой равны нулю.

22. Метод Гаусса вычисления ранга матрицы

Метод Гаусса вычисления ранга матрицы заключается в том, что путем элементарных преобразований можно привести данную матрицу А к виду

b_1l b₁₂ … b_1r … b_1n

B = 0 b₂₂ … b_2r … b_2n

…………………………… ,

0 0 … b_rr … b_rn

в котором все диагональные элементы b_1l, b₂₂, …, b_rr отличны от нуля, а элементы других строк, расположенные ниже диагональных, равны нулю.

Учитывая, что ранг не меняется при элементарных преобразованиях, имеем rang A = rang B.

Короче чтобы треугольный вид, и сколько единичек, такой и ранг

23. Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

RgA = RgA^*.

 

            Очевидно, что система (1) может быть записана в виде:

x₁  + x₂ + … + x_n

 

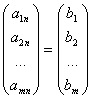
            Доказательство.

            1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход АА^* не изменяют ранга.

            2) Если RgA = RgA^*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

 

Пример. Определить совместность системы линейных уравнений:

 

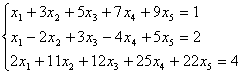
A =

 

~ .                            RgA = 2.

A* = 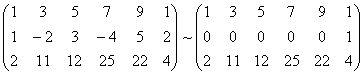          RgA* = 3.

24. Однородные системы линейных алгебраических уравнений: Свойства решений, эквивалентное преобразование системы.

Однородной системой линейных уравнений называется система вида:

Нулевое решение системы (1) называется тривиальным решением.

Однородные системы всегда совместны, т.к. всегда существует тривиальное решение.

Если существует любое ненулевое решение системы, то оно называется нетривиальным.