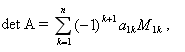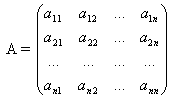1. Матрицы. Операция сложения и умножения матрицы на число

Ответ:

Опр1. Матрицей A размерности Sxn называется прямоугольная таблица из чисел, состоящая из S строк и n столбцов.

- элемент матрицы,

i – номер строки,

j – номер столбца.

Типы матриц:

1. квадратная матрица;

2. нульматрица;

3. ; A – диагональная матрица элементы главной диагонали.

4. единичная матрица.

5.

верхняя треугольная матрица.

6.

нижняя треугольная матрица

Определение2 Пусть матрицы А и В имеют одинаковую размерность, тогда

Пусть для , тогда говорят, что матрицы А и В равны: А=В.

Определение3 Пусть матрицы А и В имеют одинаковую размерность, тогда суммой матриц А и В называется матрица

С=А+В;

Определение4 Пусть , а вещественное число, тогда произведением матрицы А на число называется матрица

Свойства линейных операций над матрицами

Перестановочность:

1. А+В=В+А

2. (А+В)+С=А+(В+С);

Распределительный закон умножения

3.

4.

5. Определение5 Пусть существуют матрицы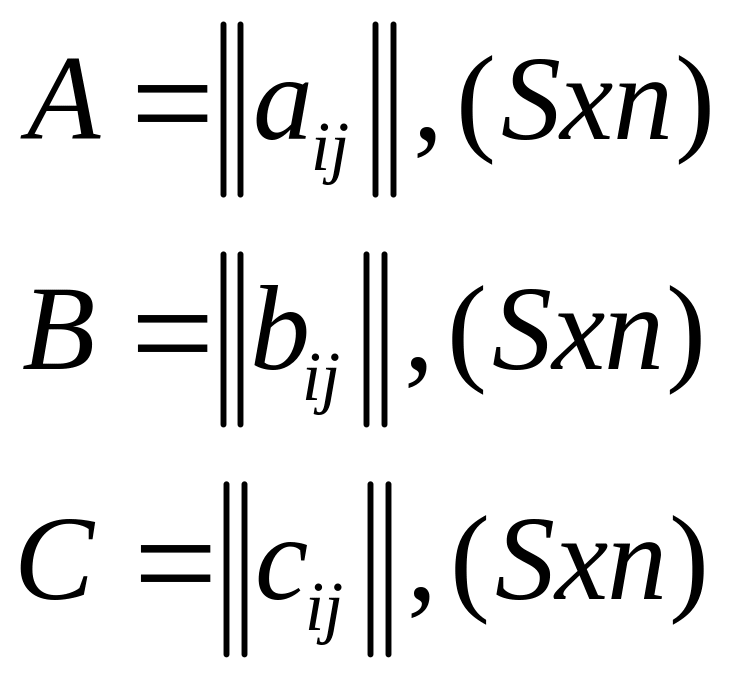

С – разность А и В, если можно записать А=В+С; обозначается С=А-В.

Определение6 Пусть матрицы

Матрица называется произведением матриц А и В (обозначается С=АВ), если

Определение7 Транспонированная матрица. Транспонировать матрицу А значит записать столбцы матрицы А строками с теми же номерами.

Вопрос 2: Операция умножения матриц и ее свойства

Определение6 Пусть матрицы

Матрица называется произведением матриц А и В (обозначается С=АВ), если

Свойства:

Сочетательное свойство:

Распределительное свойство:

.

Произведение матрицы на единичную матрицу подходящего порядка равно самой матрице:

Произведение матрицы на нулевую матрицу подходящей размерности равно нулевой матрице:

Если и — квадратные одного и того же порядка, то произведение матриц обладает ещё рядом свойств.

Умножение матриц в целом некоммутативно:

Если , то матрицы и называются перестановочными или коммутирующими между собой.

Определитель и след произведения не зависят от порядка умножения матриц:

Билет 3. Перестановки и их четность. Изменение четности при транспозиции.

Перестановки, подстановки. Понятие инверсии и четности.

Опр1. Перестановкой n-го порядка называется упорядоченная последовательность элемент перестановки элементов множества М.

Запишем все перестановки n=3 M={1,2,3}

6 – различных перестановок 3-го порядка

Утверждение существует n! различных перестановок n-го порядка.

Опр2 Говорят что элементы и образуют беспорядок(инверсию) в перестановке, если но при этом .

Пример 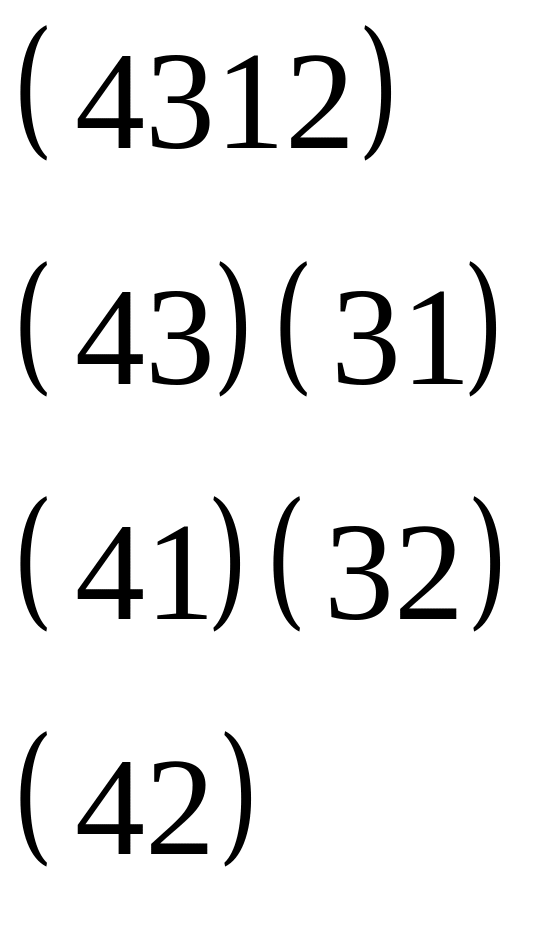всего 5 инверсий N(4312)=5.

Опр3. Транспонизацией элементов и называется перемена их местами при этом все остальные элементы фиксированы.

Утверждение Любая транспонизация элементов меняет четность перестановки.

Опр4. Подстановкой n-го порядка называется однозначное отображение множества M

Это отображение записывается в виде ;

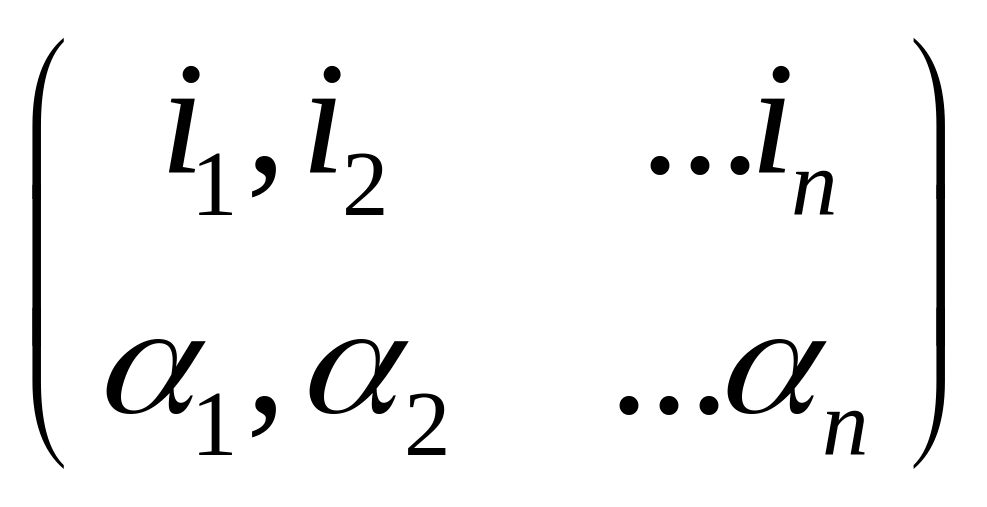Если N(p) – чётное(нечётное) число, то подстановка p называется чётной(нечётной).

Билет 4. Определители 2, 3 порядков. Определние определителя порядка n. Единичная матрица и ее определитель

Определителем квадратной матрицы (det A) называется число, которое может быть вычислено по элементам матрицы по формуле:

, где М_1k - определитель матрицы (детерминант), полученной из исходной матрицы вычеркиванием первой строки и k - oго столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов. \

В частности, формула вычисления определителя матрицы такова:

= a₁₁a₂₂a₃₃ − a₁₁a₂₃a₃₂ − a₁₂a₂₁a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂ − a₁₃a₂₂a₃₁

Определитель единичной матрицы равен 1

Билет 5.

Неизменность определителя при транспонировании его матрицы

1.Определитель не меняется при транспонировании.

Пусть А(nxn), пусть В=А^T

А=||a,ig|| , B=||b,gi||

a,ig = b,gi – очевидно.

Рассмотрим слагаемое в detB (-1)^N(P)*a£₁₁*a£₂₂*…*a£_nn

Здесь P=(1 2 … n)

(£1 £2 … £n)

произведение a£₁₁*a£₂₂*…*a£_nn входит в det A со знаком

P`=(£1 £2 … £n)

(1 2 … n)

Очевидно, что четности подстановок совпадают

(-1)^N(P)=(-1)^N(P`) по этому det A b det B состоят из одних и тех же

слагаемых произведений.

Билет 6.

Разложение определителя в сумму определителей, если какой-либо столбец определяется суммой столбцов

Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же. Например,

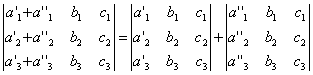
Билет 7. Свойства определителя – вынесение за знак определителя общего множителя из строки или стобца, перестановка двух строк или столбцов

Ответ:.Общий множитель элементов некоторой строки можно вынести за знак определителя.