Контрольная ОКТ, 14 вариант

В-14

1. Перевести данное число из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления. В задании д получить пять знаков после запятой в двоичном представлении.

Теоретические сведения:

Один из алгоритмов получения двоичного числа из десятичного можно описать следующим образом:

1. Исходное десятичное число делится на два (основание двоичной системы счисления).

2. В одну переменную записывается частное в виде целого числа, в другую – остаток в виде строки (если остатка нет, то записывается ноль).

3. Если частное не было равно нулю, то оно снова делится на два. Переменная, связанная со старым частным связывается с новым (прежнее частное теряется). Новый остаток с помощью операции конкатенации добавляется в начало строковой переменной, где хранятся остатки.

4. п. 3 продолжает повторяться до тех пор, пока частное не станет равно нулю.

5. Остатки от деления, записанные в обратном порядке, представляют собой двоичное представление заданного десятичного числа.

В случае перевода чисел из десятичной системы счисления в восьмеричную и шестнадцатеричную системы счисления алгоритм действий остается таким же. Но десятичное число делиться на 8 и 16 в соответствии с основанием системы счисления, в которую осуществляется перевод, а деление продолжается до тех пор, пока в результате не получиться частное равное 0 и остаток меньше 8 (при переводе в восьмеричную систему счисления) или меньше 16 (при переводе в шестнадцатеричную систему счисления).

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

1. Вначале переводится целая часть десятичной дроби в двоичную систему счисления по представленному выше алгоритму;

2. Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;

3. В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;

4. Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

В случае перевода дробного числа из десятичной системы счисления в восьмеричную и шестнадцатеричную системы счисления алгоритм действий остается таким же. Но дробная часть десятичной дроби умножается уже на 8 или 16 в соответствии с основанием системы счисления, в которую осуществляется перевод.

Решение:

а) 1047₁₀ = 10000010111₂

_ 1047 2

1046 _ 523 2

1 522 ­­­_ 261 2

1 260 _ 130 2

1 130 _ 65 2

1. 64 _ 32 2

1 32 _ 16 2

0 16 _ 8 2

0 8 _4 2

0 4 _ 2 2

0 2 1

0

1047₁₀ = 2027₈

_ 1047 8

1040 _130 8

7 128 _16 8

2 16 2

0

1047₁₀ = 417₁₆

_ 1047 16

1040 _65 16

7 64 4

1

б) 335₁₀ = 101001111₂

_ 335 2

334 _ 167 2

1 166 ­­­_ 83 2

1 82 _ 41 2

1 40 _ 20 2

1 20 _ 10 2

0 10 _ 5 2

0 4 _ 2 2

1 2 1

0

335₁₀ = 517₈

_ 335 8

328 _41 8

7 40 5

1

335₁₀ = 14F₁₆

_ 335 16

320 _ 20 16

15 16 1

4

в) 814,5₁₀ = 1100101110,1₂

_ 814 2

814 _ 407 2

0 406 _ 203 2

1 202 _101 2

1 100 _ 50 2

1 50 _25 2

0 24 _ 12 2

1 12 _ 6 2

0 6 _3 2

0 2 1

1

0,5 × 2 = 1,00

814,5₁₀ = 1456,4₈

_ 814 8

808 _ 101 8

6 96 _ 12 8

5 8 1

4

0,5 × 8 = 4,00

814,5₁₀ = 32E,8₁₆

_ 814 16

800 _ 50 16

14 48 3

2

0,5 × 16 = 8,00

г) 518,625₁₀ = 1000000110,101₂

_ 518 2

518 _ 259 2

0 258 _ 129 2

1 128 _ 64 2

1 64 _ 32 2

0 32 _16 2

0 16 _ 8 2

0 8 _ 4 2

0 4 _2 2

0 2 1

0

0,625 × 2 =1,25

0,25 × 2 = 0,50

0,5 × 2 = 1,00

518,625₁₀ = 1006,5₈

_ 518 8

512 _ 64 8

6 64 _ 8 8

0 8 1

0

0,625 × 8 = 5,00

518,625₁₀ = 206,A₁₆

_ 518 16

512 _ 32 16

6 32 2

0

0,625 × 16 = 10 = А

д) 198,91₁₀ = 11000110,11101₂

_ 198 2

198 _ 99 2

0 98 ­­­ _ 49 2

1 48 _ 24 2

1 24 _ 12 2

0 12 _ 6 2

0 6 _ 3 2

0 2 1

1

0,91 × 2 = 1,82

0,82 × 2 = 1,64

0,64 × 2 = 1,28

0,28 × 2 = 0,56

0,56 × 2 = 1,12

198,91₁₀ = 306,7217270₈

_ 198 8

192 _ 24 8

6 24 3

0

0,91 × 8 = 7,28

0,28 × 8 = 2,24

0,24 × 8 = 1,92

0,92 × 8 = 7,36

0,36 × 8 = 2,88

0,88 × 8 = 7,04

0,04 × 8 = 0,32

198,91₁₀ = C6,E8F5C2₁₆

_ 198 16

192 12

6

0,91 × 16 = 14,56 (14 = E)

0,56 × 16 = 8,96

0,96 × 16 = 15,36 (15 = F)

0,36 × 16 = 5,76

0,76 × 16 = 12,16 (12 = C)

0,16 × 16 = 2,56

2. Перевести данное число в десятичную систему счисления.

Теоретические сведения:

При переводе чисел из двоичной, восьмеричной или шестнадцатеричной систем счисления в десятичную систему счисления необходимо пронумеровать разряды целой части справа налево, начиная с нулевого, и в дробной части, начиная с разряда сразу после запятой слева направо (начальный номер -1). Затем вычислить сумму произведений соответствующих значений разрядов на основание системы счисления в степени, равной номеру разряда. Это и есть представление исходного числа в десятичной системе счисления.

Решение:

а) 1101100000₂ = 864₁₀

1101100000₂ = 1×2⁹+1×2⁸+0×2⁷+1×2⁶+1×2⁵+0×2⁴+0×2³+0×2²+0×2¹+0×2⁰ = 512 +256+0+64+32+0+0+0+0+0 = 864₁₀

б) 100001010₂ = 266₁₀

100001010₂ = 1×2⁸+0×2⁷+0×2⁶+0×2⁵+0×2⁴+1×2³+0×2²+1×2¹+0×2⁰ = 256+0+0+0+0 + 8+0+2+0 = 266₁₀

в) 1011010101₂ = 725₁₀

1011010101₂ = 1×2⁹+0×2⁸+1×2⁷+1×2⁶+0×2⁵+1×2⁴+0×2³+1×2²+0×2¹+1×2⁰ = 512+0+ 128+64+0+16+0+4+1 =725₁₀

г) 1010011111,1101₂ = 671,8125₁₀

1010011111,1101₂ = 1×2⁹+0×2⁸+1×2⁷+0×2⁶+0×2⁵+1×2⁴+1×2³+1×2²+1×2¹+1×2⁰+ 1×2^-1+1×2^-2+0×2^-3+1×2^-4 = 512+0+128+0+0+16+8+4+2+1+0,5+0,25+0+0,0625 = 671,8125₁₀

д) 452,63₈ = 298,796875₁₀

452,63₈ = 4×8²+5×8¹+2×8⁰+6×8^-1+3×8^-2 = 256+40+2+0,75+0,046875 = 298,796875₁₀

е) 1E7,08₁₆ = 487,03125₁₀

1E7,08₁₆ = 1×16²+14(E)×16¹+7×16⁰+0×16^-1+8×16^-2 = 256+224+7+0+0,03125 = 487,03125₁₀

3. Сложить числа. Проверить правильность вычислений переводом исходных данных и вычислений в десятичную систему счисления.

Теоретические сведения:

При сложении двух чисел в системе счисления с основанием q необходимо записать их столбиком одно над другим так, чтобы соответствующие разряды одного слагаемого располагался под соответствующими разрядами другого слагаемого. Сложение производится поразрядно справа налево, начиная с младших разрядов слагаемых.

Рассмотрим сложение в разряде с номером i. Введем обозначения: ai и bi - цифры соответственно первого и второго слагаемых i -го разряда, pi -признак переноса единицы из i - 1 разряда в i-ый разряд. Признак переноса pi равен 1, если в i -1 разряде сформирована единица переноса в i-ый разряд и равен 0 в противном случае. Всегда: p 0 =0. Найдем сумму: S = a + b + pi; a и b - десятичные числа, которые соответствуют цифрам ai и bi. Сложение производиться в десятичной системе счисления.

Возможны два случая: 1) S = q. Из S вычтем основание системы счисления q. Сформируем признак переноса pi+1 в следующий i +1 разряд, равный 1. Разности, полученной в результате вычитания, поставим в соответствие цифру si системы счисления с основанием q. 2) S < q. Сформируем признак переноса pi+1 в следующий i +1 разряд, равный 0. Поставим в соответствие десятичному числу S цифру si системы счисления с основанием q. Полученная цифра si является цифрой i -го разряда суммы. Аналогично производится сложение в каждом разряде.

Решение:

а) 1101100101­_2­+100010001₂

10001110110

Ответ: 1101100101­_2­+100010001₂ = 10001110110₂

Проверка:

1101100101­₂= 1×2⁹+1×2⁸+0×2⁷+1×2⁶+1×2⁵+0×2⁴+0×2³+1×2²+0×2¹+ 1×2⁰ = 512+256+0+64+32+0+0+4+0+1 = 869₁₀

100010001₂ = 1×2⁸+0×2⁷+0×2⁶+0×2⁵+1×2⁴+0×2³+0×2²+0×2¹+1×2⁰ = 256+0+ 0+0+16+0+0+0+1 = 273₁₀

10001110110₂ = 1×2¹⁰+0×2⁹+0×2⁸+0×2⁷+1×2⁶+1×2⁵+1×2⁴+0×2³+1×2²+1×2¹+ 0×2⁰ = 1024+0+0+0+64+32+16+0+4+2+0 = 1142₁₀

869₁₀+273₁₀ = 1142₁₀

б) 1100011₂+110111011₂

1000011110

Ответ: 110111011­_2­+1100011₂ = 1000011110₂

Проверка:

1100011­₂= 1×2⁶+1×2⁵+0×2⁴+0×2³+0×2²+1×2¹+1×2⁰ = 64+32+0+0+0+2+1 = 99₁₀

110111011₂ = 1×2⁸+1×2⁷+0×2⁶+1×2⁵+1×2⁴+1×2³+0×2²+1×2¹+1×2⁰ = 256+128+ 0+32+16+8+0+2+1 = 443₁₀

1000011110₂ = 1×2⁹+0×2⁸+0×2⁷+0×2⁶+0×2⁵+1×2⁴+1×2³+1×2²+1×2¹+0×2⁰ = 512+0+0+0+0+16+8+4+2+0 = 542₁₀

99₁₀+443₁₀ = 542₁₀

в) 1010101001,01₂+10011110,11₂

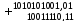
1101001000,00

Ответ: 1010101001,01₂+10011110,11₂= 1101001000,00₂

Проверка:

1010101001,01₂ = 1×2⁹+0×2⁸+1×2⁷+0×2⁶+1×2⁵+0×2⁴+1×2³ +0×2²+0×2¹+1×2⁰ +0×2^-1+1×2^-2 = 512+0+128+0+32+0+8+0+0+1+0+0,25 = 681,25₁₀

10011110,11₂ = 1×2⁷+0×2⁶+0×2⁵+1×2⁴+1×2³+1×2²+1×2¹+0×2⁰+1×2^-1 +1×2^-2 = 128+ 0+0+16+8+4+2+0+0,5+0,25 = 158,75₁₀

1101001000,00₂ = 1×2⁹+1×2⁸+0×2⁷+1×2⁶+0×2⁵+0×2⁴+1×2³+0×2²+0×2¹+0×2⁰+ 0×2^-1 +0×2^-2 = 512+256+0+64+0+0+8+0+0+0+0+0 = 840₁₀

681,25₁₀+158,75₁₀ = 840₁₀

г) 1672,2₈+266,2₈

2160,4

Ответ: 1672,2₈+266,2₈= 2160,4₈

Проверка:

1672,2₈ = 1×8³+6×8²+7×8¹+2×8⁰+2×8^-1 = 512+384+56+0,25 = 954,25₁₀

266,2₈ = 2×8²+6×8¹+6×8⁰+2×8^-1 =128+48+6+0,25 = 182,25₁₀

2160,4₈ = 2×8³+1×8²+6×8¹+0×8⁰+4×8^-1 = 1024+64+48+0+0,5 = 1136,5₁₀

954,25₁₀+182,25₁₀ = 1136,5₁₀

д) 18B,A₁₆+2E9,2₁₆

474,C

Ответ: 18B,A₁₆+2E9,2₁₆ = 474,C₁₆

Проверка:

18B,A₁₆ = 1×16²+8×16¹+11(B)×16⁰+10(A)×16^-1 = 256+128+11+0,625 = 395,625₁₀

2E9,2₁₆ = 2×16²+14(E)×16¹+9×16⁰+2×16^-1 = 512+224+9+ 0,125 = 745,125₁₀

474,C₁₆ = 4×16²+7×16¹+4×16⁰+12(C)×16^-1 = 1024+112+4+ 0,75 = 1140,75₁₀

395,625₁₀+745,125₁₀ = 1140,75₁₀

4. Выполнить вычитание. Проверить правильность вычислений переводом исходных данных и вычислений в десятичную систему счисления.

Теоретические сведения:

Для того чтобы вычесть числа в системе счисления с основанием q , необходимо записать одно число под другим столбиком, чтобы разряды вычитаемого располагались под соответствующими разрядами уменьшаемого. Вычитание производиться поразрядно, начиная с младшего разряда.

Рассмотрим вычитание в i -ом разряде. Введем обозначения: ai и bi - цифры соответствующие уменьшаемому и вычитаемому i -го разряда, p - признак единицы заёма в i –ом разряде. Признак заёма p равен - 1, если возникла необходимость в заёме единицы в i + 1 разряде и признак pi равен 0 в противном случае. Для нулевого разряда всегда выполняется p 0 =0. Поставим в соответствии ai и bi десятичные числа a и b. Найдем значение выражения R = a - b + p .

Возможны два случая : 1) R < 0. Признаку заема присвоим значение равное –1: pi+1 = -1, т.е. возникает заем единицы из следующего разряд а. Найдем сумму R + q. Полученной сумме поставим в соответствие цифру ri системы счисления с основанием q. 2) R = 0 . Значению r необходимо поставить в соответствие цифру ri. Признаку заема присвоить значение равное нулю: pi+1 = 0. Полученная цифра ri является цифрой i -го разряда разности. Аналогично производится вычитание в каждом разряде.

Решение:

а) 1110111011₂ – 100110111₂

1010000100

Ответ: 1110111011₂ – 100110111₂ = 1010000100₂

Проверка:

1110111011₂ = 1×2⁹+1×2⁸+1×2⁷+0×2⁶+1×2⁵+1×2⁴+1×2³ +0×2²+1×2¹+1×2⁰ = 512+256+128+0+32+16+8+0+2+1 = 955₁₀

100110111₂ = 1×2⁸+0×2⁷+0×2⁶+1×2⁵+1×2⁴+0×2³+1×2²+1×2¹+1×2⁰= 256+ 0+0+32+16+0+4+2+1 = 311₁₀

1010000100₂ = 1×2⁹+0×2⁸+1×2⁷+0×2⁶+0×2⁵+0×2⁴+0×2³+1×2²+0×2¹+0×2⁰ = 512+0+128+0+0+0+0+4+0+0= 644₁₀

955₁₀ – 311₁₀ = 644₁₀

б) 1110000101₂ – 1001110₂

1100110111

Ответ: 1110000101₂ – 1001110₂ = 1100110111₂

Проверка:

1110000101₂ = 1×2⁹+1×2⁸+1×2⁷+0×2⁶+0×2⁵+0×2⁴+0×2³ +1×2²+0×2¹+1×2⁰ = 512+256+128+0+0+0+0+4+0+1 = 901₁₀

1001110₂ = 1×2⁶+0×2⁵+0×2⁴+1×2³+1×2²+1×2¹+0×2⁰= 64+ 0+0+8+4+2+0 = 78₁₀

1100110111₂ = 1×2⁹+1×2⁸+0×2⁷+0×2⁶+1×2⁵+1×2⁴+0×2³+1×2²+1×2¹+1×2⁰ = 512+256+0+0+32+16+0+4+2+1= 823₁₀

901₁₀ – 78₁₀ = 823₁₀

в) 1011110100,0011₂ – 101001011,001₂

110101001,0001

Ответ: 1011110100,0011₂ – 101001011,001₂ = 110101001,0001₂

Проверка:

1011110100,0011₂ = 1×2⁹+0×2⁸+1×2⁷+1×2⁶+1×2⁵+1×2⁴+0×2³ +1×2²+0×2¹+0×2⁰ +0×2^-1 +0×2^-2+1×2^-3+1×2^-4 = 512+0+128+64+32+16+0+4+0+0+0+0+0,125+

0,0625 = 756,1875₁₀

101001011,001₂ = 1×2⁸+0×2⁷+1×2⁶+0×2⁵+0×2⁴+1×2³ +0×2²+1×2¹+1×2⁰ +0×2^-1 +0×2^-2+1×2^-3 = 256+0+64+0+0+8+0+2+1+0+0+0,125 = 331,125₁₀

110101001,0001₂= 1×2⁸+1×2⁷+0×2⁶+1×2⁵+0×2⁴+1×2³ +0×2²+0×2¹+1×2⁰ +0×2^-1 +0×2^-2+0×2^-3+1×2^-4 = 256+128+0+32+0+8+0+0+1+0+0+0 +0,0625 = 425,0625₁₀

756,1875₁₀ –331,125₁₀ = 425,0625₁₀

г) 1560,22₈ – 1142,2₈

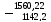
416,02

Ответ: 1560,22₈ – 1142,2₈= 416,02₈

Проверка:

1560,22₈ = 1×8³+5×8²+6×8¹+0×8⁰+2×8^-1+2×8^-2 = 512+320+48+0,25+0,03125 = 880,28125₁₀

1142,2 ₈ = 1×8³+1×8²+4×8¹+2×8⁰+2×8^-1=512+64+32+2+0,25 = 610,25₁₀

416,02₈ = 4×8²+1×8¹+6×8⁰+0×8^-1+2×8^-2 = 256+8+48+0+0,03125 = 270,03125₁₀

880,28125₁₀+610,25₁₀= 270,03125₁₀

д) 1A5,8₁₆ – 7D,A₁₆

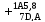
127,E

Ответ: 1A5,8₁₆ – 7D,A₁₆ = 127,E ₁₆

Проверка:

1A5,8₁₆ = 1×16²+10(A)×16¹+5×16⁰+8×16^-1 = 256+160+5+0,5 = 421,5₁₀

7D,A₁₆ = 7×16¹+13(D)×16⁰+10(A)×16^-1 = 112+13+ 0,625 = 125,625₁₀

127,E₁₆ = 1×16²+2×16¹+7×16⁰+14(E)×16^-1 = 256+32+7+ 0,875 = 295,875₁₀

421,5₁₀ – 125,625₁₀ = 295,875₁₀

5. Выполнить умножение. Проверить правильность вычислений переводом исходных данных и вычислений в десятичную систему счисления.

Теоретические сведения:

Для выполнения умножения в различных системах счисления необходимо иметь соответствующие таблицы умножения. Для двоичной, восьмиричной и шестнадцатиричной систем счисления таблицы представлены ниже.

Рисунок 1 – Таблица умножения для двоичной системы счисления

Рисунок 2 – Таблица умножения для восьмеричной системы счисления

Рисунок 3 – Таблица умножения для шестнадцатеричной системы счисления

Решение:

а) 111100₂×111100₂

000000

000000

111100

111100

111100

111100

111000010000

Ответ: 111100₂×111100₂ = 111000010000₂

Проверка:

111100₂ = 1×2⁵+1×2⁴+1×2³+1×2²+0×2¹+0×2⁰= 32+ 16+8+4+0+0 = 60₁₀

111000010000₂ = 1×2¹¹+1×2¹⁰+1×2⁹+0×2⁸+0×2⁷+0×2⁶+0×2⁵+1×2⁴+0×2³+0×2²+0×2¹+0×2⁰ = 2048+1024+512+0+0+0+0+16+0+0+0+0= 3600₁₀

60₁₀ × 60₁₀ = 3600₁₀

б) 274,5₈×31,34₈

13624

10657

2745

10657

11276,114

Ответ: 274,5₈×31,34₈= 11276,114₈

Проверка:

274,5₈ = 2×8²+7×8¹+4×8⁰+5×8^-1 = 128+56+4+0,625 = 188,625₁₀

31,34₈ = 3×8¹+1×8⁰+3×8^-1+4×8^-2 =24+1+0,375+0,0625= 25,4375₁₀

11276,114₈= 1×8⁴+1×8³+2×8²+7×8¹+6×8⁰+1×8^-1+1×8^-2+4×8^-3 = 4096+512+128+56+6+0,125+0,015625+0,0078125= 4798,1484375₁₀

188,625₁₀×25,4375₁₀= 4798,1484375₁₀

в) 13,4₁₆×38,48₁₆

9A0

4D0

9A0

39C

43B,6A0

Ответ: 13,4₁₆×38,48₁₆= 43B,6A₁₆

Проверка:

13,4₁₆= 1×16¹+3×16⁰+4×16^-1 = 16+3+0,25 = 19,25₁₀

38,48₁₆= 3×16¹+8×16⁰+4×16^-1+8×16^-2 = 48+8+0,25+ 0,03125= 56,28125₁₀

43B,6A₁₆= 4×16²+3×16¹+11(B)×16⁰+6×16^-1 +10(A)×16^-2 = 1024+48+11+ 0,375+0,0390625= 1083,4140625 ₁₀

19,25₁₀×56,28125₁₀= 1083,4140625 ₁₀

6. Выполнить деление. Проверить правильность вычислений переводом исходных данных и вычислений в десятичную систему счисления.

Теоретические сведения:

Для выполнения деления можно использовать таблицы умножения, представленные на рисунках 1, 2 и 3.

Решение:

a) 10011101100₂ : 1110₂

_10011101100 1110

1110 1011010

_10110

1110

_10001

1110

_1110

1110

0

Ответ: 10011101100₂ : 1110₂= 1011010₂

Проверка:

10011101100₂ = 1×2¹⁰+0×2⁹+0×2⁸+1×2⁷+1×2⁶+1×2⁵+0×2⁴+1×2³+1×2²+0×2¹+ 0×2⁰ = 1024+0+0+128+64+32+0+8+4+0+0= 1260₁₀

1110₂ = 1×2³+1×2²+1×2¹+0×2⁰= 8+4+2+0 = 14₁₀

1011010₂ = 1×2⁶+0×2⁵+1×2⁴+1×2³+0×2²+1×2¹+0×2⁰ = 64+0+16+8+0+2+0= 90₁₀

1260₁₀ × 14₁₀ = 90₁₀

б) 1436₈ : 23₈

_1436 23

137 52

_46

46

0

Ответ: 1436₈ : 23₈= 52 ₈

Проверка:

1436₈= 1×8³+4×8²+3×8¹+6×8⁰ = 512+256+24+6 = 798₁₀

23₈ = 2×8¹+3×8⁰ = 16+3= 19₁₀

52₈= 5×8¹+2×8⁰ = 40+2= 42₁₀

798₁₀: 19₁₀= 42₁₀

в) CD6₁₆ : 1F₁₆

_CD6 1F

BA 6A

_136 _

136

0

Ответ: CD6₁₆ : 1F₁₆= 6A₁₆

Проверка:

CD6₁₆= 12(C)×16²+D(13)×16¹+6×16⁰= 3072+208+6 = 3286₁₀

1F₁₆= 1×16¹+15(F)×16⁰ = 16+15= 31₁₀

6A₁₆= 6×16¹+10(A)×16⁰ = 96+10= 106 ₁₀

3286₁₀ : 31₁₀= 106 ₁₀

Список литературы

1. Ковриженко, Г. А. Системы счисления и двоичная арифметика: Радянська школа, 1984. – 82 с.

2. Арифметические операции в позиционных системах счисления, электронное пособие http://www.5byte.ru

3. Дидактические материалы по информатике и математике http://comp-science.narod.ru

Контрольная работа выполнена 25.10.2011