
-
Предопределенные процессы. Рекурсия.
Рекурсия — это такой способ организации подпрограммы, при котором эта подпрограмма (процедура или функция) в ходе выполнения ее операторов обращается сама к себе. Такая рекурсия называется прямой. Есть также косвенная рекурсия, когда две или более подпрограмм вызывают друг друга.
Для выражения рекурсивных программ удобнее пользоваться процедурами или функциями.
Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.
Следует избегать избыточной глубины рекурсии, так как это может вызвать переполнение стека вызовов.
Максимальная глубина рекурсии должна быть не только конечна, но и достаточно мала. Так как каждая рекурсивная активация подпрограммы требует памяти для размещения ее переменных. Кроме этих переменных нужно еще сохранять текущее "состояние вычислений", чтобы можно было вернуться в него по окончании новой активации этой подпрограммы.
При обращении подпрограммы самой к себе происходит то же самое, что и при обращении к любой другой функции или процедуре: в стек записывается адрес возврата, резервируется место под локальные переменные, происходит передача параметров, после чего управление передается первому исполняемому оператору подпрограммы. При повторном вызове этот процесс повторяется. Ясно, что для завершения вычислений каждая рекурсивная подпрограмма должна содержать хотя бы одну нерекурсивную ветвь алгоритма, заканчивающуюся возвратом в вызывающую программу.
При завершении подпрограммы область её локальных переменных освобождается, а управление передается на оператор, следующий за рекурсивным вызовом.
Алгоритм, который содержит обращение к самому себе, называется рекурсивным алгоритмом.
В таких алгоритмах выделяется два этапа выполнения:
1) «погружение» алгоритма в себя, то есть использование определения «в другую сторону», пока не будет найдено начальное определение, не являющееся рекурсивным;
2) последовательное выполнение операций от начального определения до определения с введенным в алгоритм значением.
Задачи:
1. Задан целочисленный одномерный массив a из n элементов. Найти номер последнего максимального элемента среди положительных элементов, начиная с первого элемента, большего заданного числа Т.












i < n







i=i+1




i








i<n



i=i+1




i 





var=a[0]

number=-1






i< n



нет да




var=a[i]
number=i






i=i+1





 i
i


нет да










29. Дана целочисленная квадратная матрица. Определить сумму элементов в тех строках, которые не содержат отрицательных элементов.

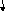








 i<
n
i<
n







j< n




j=j+1





 j
j


i=i+1





 i
i



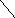


 i<
n
i<
n














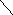
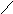























j< n







j=j+1





 j
j


i=i+1





 i
i


count=0

summa=0




 i<
n
i<
n





 j<
n
j<
n



нет да




count ++






j=j+1





 j
j



нет да








 j<
n
j<
n


summa+=mass[i][j]

j=j+1





 j
j




summa=0



count=0

i=i+1




i




