
- •Ограниченные и неограниченные множества. Примеры.
- •2) Для любого положительного числа в множестве m можно найти число , такое что
- •Арифметика бесконечно малых последовательностей.
- •Доказательство:
- •9) Свойства сходящихся последовательностей: предельный переход в неравенства.
- •13) Подпоследовательности, частичные пределы. Связь предела последовательности с частичными пределами.
- •Доказательство: (метод деления пополам).
- •Доказательство:
- •Доказательство:
Доказательство:
Возьмем
число
>0.
Так как функция
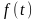 непрерывна
в точке
то
можно подобрать такое число
непрерывна
в точке
то
можно подобрать такое число
 ,
что
,
что
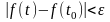 для
любого
для
любого
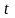 ,
такого, что
,
такого, что
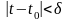 .
(1)
.
(1)
А
так как функция
непрерывна в точке
,
то для положительного числа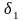 можно подобрать такое число
можно подобрать такое число
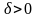 ,
что
,
что
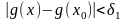 для
любого
,
такого, что
.
(2)
для
любого
,
такого, что
.
(2)
Возьмем
любое число
такое, что
.
Тогда в силу (2)
число
удовлетворяет неравенству
,
и поэтому в силу (1)
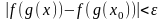 .
Так как все эти вычисления проведены
для любого
>0,
то непрерывность функции
в точке
доказана.
.
Так как все эти вычисления проведены
для любого
>0,
то непрерывность функции
в точке
доказана.
30) Классификация точек разрыва.
Определение: -точка разрыва функции , если в точке функция не является непрерывной.
Определение:
точка
-точка
устранимого разрыва функции
,
если существует
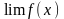 ,
но
не
определена в точке
,
либо
,
но
не
определена в точке
,
либо
 .
.
Замечание: Если в точке устранимого разрыва доопределить (переопределить) функцию:

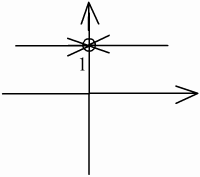 -
непрерывна в точке
.
-
непрерывна в точке
.
Пример:
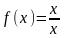 .
.
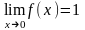 ,
,
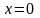 -
точка устранимого разрыва
.
-
точка устранимого разрыва
.
Если не существует, то -точка неустранимого
разрыва .
Определение: Пусть точка -точка неустранимого разрыва функции , тогда:
если существует
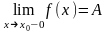 ,
то
,
то
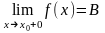 .
.если
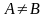 ,
то
-точка
разрыва функции
1-го рода.
,
то
-точка
разрыва функции
1-го рода.если
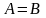 ,
то
-точка
разрыва функции
2-го рода.
,
то
-точка
разрыва функции
2-го рода.
П римеры:
римеры:
1).
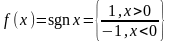 .
.
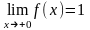 ,
,
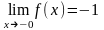
- точка разрыва 1-го рода.
2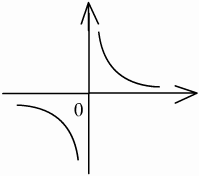 ).
).
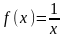 .
.
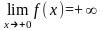 ,
,
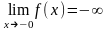
- точка разрыва 2-го рода.
3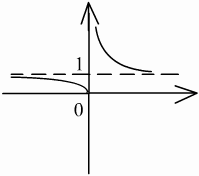 ).
).
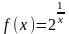
,
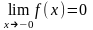
- точка разрыва 2-го рода.
4 ).
).
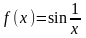
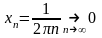
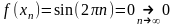
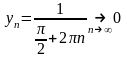
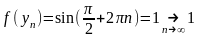
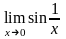 не
существует
точка
-
точка разрыва
2-го
рода.
не
существует
точка
-
точка разрыва
2-го
рода.
, . Точка - точка разрыва 2-го рода.
31) Точки разрыва монотонной функции.
32)
Первая теорема Вейерштрасса.
Пусть
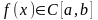 .
Тогда
ограничена
на
.
Тогда
ограничена
на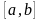 .
.
Доказательство:
Докажем,
что
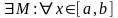
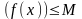 .
.
Предположим
противное, то есть
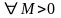
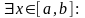
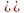 .
Возьмем
=1,2,3…
.
Возьмем
=1,2,3…
Получим :
1)
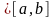
2)
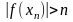
Из
этих определений получаем
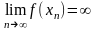 .
.
=>
 -подпоследовательность
последовательности
:
-подпоследовательность
последовательности
:
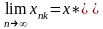 .
.
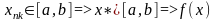 -непрерывна
в точке
-непрерывна
в точке
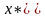 =>
=>
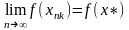 .
.
-подпоследовательность
последовательности
:
=>
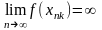 .
Противоречие.
.
Противоречие.
Замечание:
Замкнутость
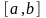 по
существу.
по
существу.
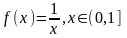 ,
,
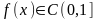 ,
но
,
но
Не
является ограниченной на
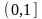 .
.
33) Вторая теорема Вейерштрасса.
Пусть
.
Тогда
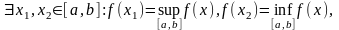
Замечание: Непрерывная на отрезке функция на этом отрезке достигает своего наибольшего и наименьшего значения, причем в условиях теоремы отрезок по существу.
Доказательство:
По
условию теоремы
=>
ограничена
на
=>
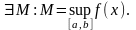 Докажем, что
Докажем, что
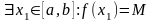 .
Предположим противное, то есть
.
Предположим противное, то есть
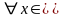
 .
Рассмотрим вспомогательную функцию
.
Рассмотрим вспомогательную функцию
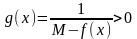 на
.
По 1 теореме Вейерштрасса
на
.
По 1 теореме Вейерштрасса
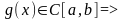 ограничена
на
,
то есть
ограничена
на
,
то есть
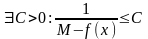 .
.
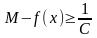
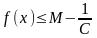
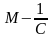 (<
)-
верхняя граница.
(<
)-
верхняя граница.
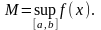 ,
то есть
,
то есть
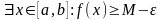 .
.
Противоречие.
Следствие:
если
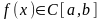 ,
то
,
то
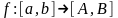 .
.
34) Теорема о нуле непрерывной функции.
35) Теорема Больцано-Коши, ее следствия.
36) Критерий непрерывности монотонной функции.
37) Непрерывность обратной функции.
