Арифметика бес­конечно малых последовательностей.

Теорема: сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.

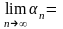
Пусть . Возьмем произвольный .

Аналогично

.

Обозначим .

Тогда .

То есть

Теорема: произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.

, - ограниченная, то есть .

Возьмем произвольный .

- бесконечно малая.

.

Обозначим . Тогда

.

То есть

Замечание: сходимость ограниченной последовательности здесь не требуется.

5) Б.б. последовательности и их связь с б.м. Определение. Последовательность {x_n} называется бесконечно большой, если для любого положительного числа A можно указать номер N такой, что при   все элементы x_n этой последовательности удовлетворяют неравенству   .

Любая бесконечно большая последовательность является неограниченной. Но не каждая неограниченная последовательность является бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3, ... 1, n, ... не является бесконечно большой, так как при A > 1 неравенство   не выполняется для x_n с нечетными номерами.

6) Арифметические свойства пределов последовательностей (предел суммы, предел произведения).

Определение.

Последовательность называется сходящейся, если она имеет конечный предел. В противном случае (если предел бесконечный или не существует)- расходящаяся последовательность

Теорема 1.

Пусть { }, { } – сходящиеся последовательности, тогда последовательности { };{ };{ }-сходятся, причем ; .

Доказательство.

1. Для { } .

Последовательность { } сходится , где { } – бесконечно малая последовательность.

Последовательность { } сходится , где { } – бесконечно малая последовательность(б.м.п.).

Рассмотрим . Обозначим . { }, { } - б.м.п. б.м.п. - б.м.п..

Таким образом

2. Для { }.

Аналогично: , { }- б.м.п., , { }- б.м.п. . Обозначим . { },{ } - б.м.п. - б.м.п. - б.м.п..

Таким образом - б.м.п. .

7) Арифметические свойства пределов последовательностей (предел частного).

если то существует .

Док-во: где

- бесконечно малая последовательность.

По условию

-ограниченная.

бесконечно малая.

.

8) Свойства сходящихся последовательностей: единственность предела, ограниченность сходящейся последовательности.

Теорема: (о единственности предела): Если -сходящаяся, то предел единственный.

Доказательство:

Пусть , , .

Для определенности имеем:

.

< <

< . < .

Противоречие.

Теорема: (об ограниченности сходящейся последовательности): Если -сходится, то она ограничена.

- сходящаяся : .

Возьмем =1 .

Обозначим , тогда

, тогда

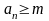
Отсюда для обоих случаев

Замечание: обратное не верно.