
- •Ограниченные и неограниченные множества. Примеры.
- •2) Для любого положительного числа в множестве m можно найти число , такое что
- •Арифметика бесконечно малых последовательностей.
- •Доказательство:
- •9) Свойства сходящихся последовательностей: предельный переход в неравенства.
- •13) Подпоследовательности, частичные пределы. Связь предела последовательности с частичными пределами.
- •Доказательство: (метод деления пополам).
- •Доказательство:
- •Доказательство:
13) Подпоследовательности, частичные пределы. Связь предела последовательности с частичными пределами.
Билет № 13. Подпосл-ти, частичные пределы, связь предела посл-тей с частичным пределом.
Пусть
дана посл-ть {
}.
Выбираем элементы с номером
![]() <
<![]() <
<![]() <
<![]() => числа {
=> числа {![]() ,
,![]() ,
,…}
образуют посл-ть {
,
,…}
образуют посл-ть {![]() }.
}.
Утверждение.
![]() =a}{для
любой её подпосл-ти {
=a}{для
любой её подпосл-ти {![]() }
}
![]() }.
}.
Доказательство.
=>![]() =a
=>
=a
=> ![]()
Рассмотрим
![]() }.
}.
![]() |
-a|<
|
-a|<![]()
![]() .
.
Таким образом
![]() =>
=>![]()
<= Для
}
![]() =a.
=a.
{
}
также подпосл-ть посл-ти {
}=>![]() .
.
Замечание 1. Аналогичное утверждение для бесконечно больших посл-тей, т.е. посл-ть { } явл. б.б. => } явл. б.б.
Замечание 2.
Пусть {![]() }
имеет две сх-ся подпосл-ти {
}
имеет две сх-ся подпосл-ти {![]() }
и {
}
и {![]() },
такие что
},
такие что ![]() ,
тогда
,
тогда ![]() .
.
Предположим
противное, т.е. ![]() =a
=> тогда по теорме
=a
=> тогда по теорме ![]() =a,
получаем противоречие, след-но
=a,
получаем противоречие, след-но ![]() .
.
Частичный предел пол-ти.
Определение. Бесконечный и конечный предел определённого знака наз-ся частичным пределом посл-ти { }.
Понятие о верхнем и нижнем пределе.
Мн-во
действительных чисел R,
заполненное эл-ми {+![]() }
и {-
}
пределов, наз-ся расширенным мн-вом
действительных чисел.
}
и {-
}
пределов, наз-ся расширенным мн-вом
действительных чисел.
Определение.
Наибольшим в ![]() частичный предел посл-ти наз-ся её
верхним пределом и обозначается
частичный предел посл-ти наз-ся её
верхним пределом и обозначается ![]() .
Наименьшим в
частичным пределом посл-ти наз-ся её
нижним пределом и обозначается
.
Наименьшим в
частичным пределом посл-ти наз-ся её
нижним пределом и обозначается ![]() .
.
14) Теорема Больцано-Вейерштрасса.
Теорема: Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Доказательство: (метод деления пополам).
I). Проведем построение системы отрезков.
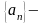 ограниченная
ограниченная

 .
.
Рассмотрим
точку
 -
середину отрезка
-
середину отрезка
 .
.
1)
В отрезке содержится бесконечное число элементов
.
содержится бесконечное число элементов
.
Тогда
 ,
,
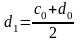 .
.
2)
В противном случае
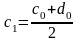 ,
,
 ,
,
 -содержит бесконечное число элементов
.
-содержит бесконечное число элементов
.
Рассмотрим
точку
 -
середину
-
середину
 и
так далее.
и
так далее.
1.
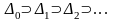
2.
в
 содержится бесконечное число элементов
.
содержится бесконечное число элементов
.
3.
 .
.
II). Выбор подпоследовательности
По
лемме о вложенных отрезках:
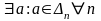
1)
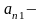 произвольный
элемент из
произвольный
элемент из
2)
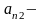 элемент
из
элемент
из
 :
:
………………………………………………….
k)
 элемент
из
элемент
из
 :
:

Докажем,
что
 .
.

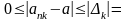
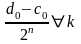
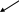
0
( ).
).
.
15) Критерий Коши сходимости числовой последовательности.
Теорема (критерий Коши): Числовая последовательность сходится тогда и только тогда, когда она фундаментальна.
Замечание: Условие необходимости (=>), условие достаточности (<=), критерий- условие необходимости и достаточности (<=>).
1) Необходимость: (=>).
Пусть
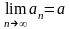 .
Возьмем произвольный
.
Возьмем произвольный
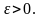 Тогда
Тогда

 .
.
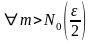
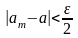 .
Обозначим
.
Обозначим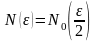 ,
тогда
,
тогда

 .
.
фундаментальна.
2) Достаточность: (<=).
1.
фундаментальна
=>
ограниченная

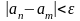 .
.
Возьмем
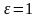 ,
,
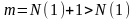 ,
тогда
,
тогда
 .
.
Обозначим
 .
.
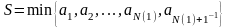 .
.
 ограничена.
ограничена.
2. Теорема Больцано-Вейерштрасса.
ограниченная
=>
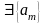 -
сходящаяся. Обозначим
-
сходящаяся. Обозначим

3. Докажем, что
Возьмем
произвольный
.
фундаментальная
=>

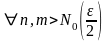
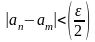 .
.




Обозначим
и выберем
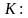
k>K

Тогда
 .
.
 .
То есть
.
То есть
16) Предел функции: два определения и их эквивалентность.
Пусть
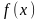 определена
в некоторой выколотой
определена
в некоторой выколотой
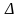 окрестности
т.
окрестности
т.

Определение
1 (Гейне):
 ,
если
,
если
 ,
,
 ,
,

Замечание:
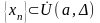
Определение
2 (Коши):
,
если

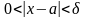 .
.
 .
.
Замечание:
 ,
то есть
,
то есть
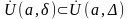 .
.
Теорема: Определение 1 <=> Определение 2.
Имеем
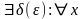 .
.
.
.
Возьмем
произвольную
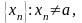
 =
=>
=
=>
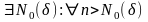
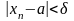 .
.
Обозначим
 .
Тогда
0<
.
Тогда
0< .
.
Т.обр.

 .,
то есть
.,
то есть
17) Арифметические свойства предела функции.
Теорема:
Если существуют
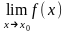 и
и
 ,
то:
,
то:
1).
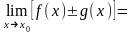
 .
.
2).
 =
=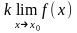 (
(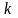 -
постоянная).
-
постоянная).
3).
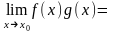 *
.
*
.
4).


 ,
если
,
если
 .
.
Доказательства:
Доопределив
по непрерывности функции
и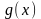 в точке
в точке
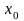 ,
положив
,
положив
 =
и
=
и
 =
(это изменение функций не влияет на их
пределы). В точке
будут непрерывны функции
=
(это изменение функций не влияет на их
пределы). В точке
будут непрерывны функции
 ,
,
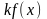 ,
,
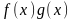 ,
,
 (так как
=
.
Поэтому в силу равенства
=
получим:
(так как
=
.
Поэтому в силу равенства
=
получим:
1).
 =
.
=
.
2).
= =
=
3).
 =
*
.
=
*
.
4).
 =
.
=
.
18) Свойства предела функции: единственность предела; ограниченность функции, имеющей предел.
19) Свойства предела функции: предельные переходы в неравенства.
20) Односторонние пределы.
21) Первый замечательный предел.
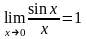
Для
доказательства возьмем вектор
 окружности радиуса 1 с центральным
углом, равным
окружности радиуса 1 с центральным
углом, равным
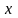 (радиан),
(радиан),
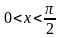 и проведем
и проведем
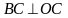 .
Тогда пл.
<
пл. сект.
<
пл.
.
Тогда пл.
<
пл. сект.
<
пл.
 или
или
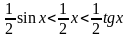 .
Разделив все части этого неравенства
на
.
Разделив все части этого неравенства
на
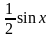 >
0, получим
>
0, получим
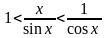 или
или
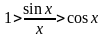 .
Это неравенство, доказанное для любых
из интервала (0;
.
Это неравенство, доказанное для любых
из интервала (0;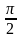 ),
верно для любого
),
верно для любого
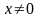 из
интервала (-
;
)
в силу четности функций, входящих в это
неравенство.
из
интервала (-
;
)
в силу четности функций, входящих в это
неравенство.
Докажем,
что
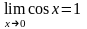
( )
при
)
при
А
раз
и
 ,
то
.
,
то
.
Кроме
того:
 =
=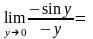 1
1
22) Второй замечательный предел.
.
На
первый взгляд кажется, что
при
имеет пределом единицу (так как 1+
при
имеет пределом единицу, а единица в
любой степени есть единица). Но в степень
 возводится
1+
,
а не единица. И вот из-за этой бесконечно
малой добавки
предел не равен единице. Чтобы
приблизительно представить себе
поведение функции
при
малых
приведем таблицу значений этой функции:
возводится
1+
,
а не единица. И вот из-за этой бесконечно
малой добавки
предел не равен единице. Чтобы
приблизительно представить себе
поведение функции
при
малых
приведем таблицу значений этой функции:
|
1/2 |
1/3 |
1/4 |
0.01 |
0.001 |
|
2.25 |
2.37… |
2.44… |
2.7047… |
2.7169… |
Из этой таблицы видно, что с уменьшением функция увеличивается. Оказывается, что это имеет место для всех >0, а из этого следует, что функция имеет предел.
Доказательство:
Рассмотрим этот предел, как предел функции натурального аргумента на бесконечность. Тогда:
По определению Гейне:
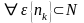

 =
=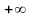

 =
=
Вычислим
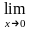 .
Рассмотрим
=
.
Рассмотрим
=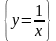 =
=
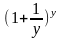 .
.
По
определению Гейне рассмотрим
 .
.





 *
*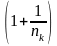
То
есть
=
=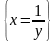 =
.
=
.
Т акже
=
акже
= =
=
 =
=
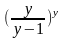 =
=

1
23) Б.м. функции и их свойства.
Определение:
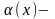 бесконечно
малая функция при
бесконечно
малая функция при
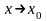 ,
если
,
если
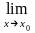
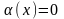 .
.
Определение:
Пусть
 и
и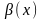 -
бесконечно малые функции при
.
Тогда:
-
бесконечно малые функции при
.
Тогда:
1)
и
эквивалентны при
(
~
,
),
если
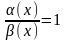 .
.
2)
,
-
бесконечно малые одного порядка малости
при
,
если
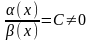 .
3)
-
бесконечно малая более высокого порядка
малость, чем
.
.
3)
-
бесконечно малая более высокого порядка
малость, чем
.
(
=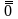 (
),
),
если
(
),
),
если
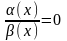 .
.
4).
имеет
-й
порядок малости относительно
при
,
если
 .
.
5).
называется ограниченной относительно
бесконечно малой функции
при
,
если

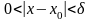
 .
.
Примеры:
1).
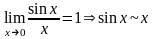 при
при
 .
.
2).
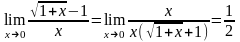 (
( ,
-бесконечные
малости одного порядка).
,
-бесконечные
малости одного порядка).
3
).
 (
(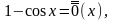
 )
)
1 0
4). …
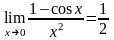 (
( )-
2-й порядок малости относительно
при
.
)-
2-й порядок малости относительно
при
.
5).

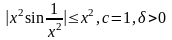 -
произвольная.
-
произвольная.
24) Б.б. функции и их связь с б.м. функциями.
25) Сравнение б.м. функций. Примеры.
Определение: бесконечно малая функция при , если .
Определение: Пусть и - бесконечно малые функции при . Тогда:
1) и эквивалентны при ( ~ , ), если .
2) , - бесконечно малые одного порядка малости при , если . 3) - бесконечно малая более высокого порядка малость, чем .
( = ( ), ), если .
4). имеет -й порядок малости относительно при , если .
5). называется ограниченной относительно бесконечно малой функции при , если .
Примеры:
1). при .
2). ( , -бесконечные малости одного порядка).
3 ). ( )
1 0
4). …
( )- 2-й порядок малости относительно при .
5).
- произвольная.
26) Эквивалентные б.м. функции (таблица). Теорема об эквивалентных б.м. функциях.
Определение:
функция
называется
бесконечно
малой
при
,
если
 =0.
=0.
Теорема (критерий эквивалентности):
Пусть , -бесконечно малые функции при .
 -
.
Тогда
~
при
-
.
Тогда
~
при
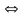
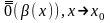 .
.
Доказательства:
( ). Пусть ~ , , то есть .
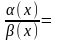

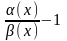 =0,
=0,
то есть .
(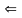 ).
.,
.
).
.,
.
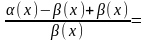
 =1.
=1.
Теорема (о замене на эквивалентные):
Пусть
функция
~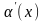 ,
~
,
~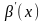 при
и существует
при
и существует
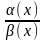 ,
тогда существует и
,
тогда существует и
 =
.
То есть выражение или функцию можно
заменять на эквивалентное.
=
.
То есть выражение или функцию можно
заменять на эквивалентное.
=
* *
* =
.
=
.

1 1
27) Сравнение б.б. функций. Примеры.
28) Непрерывность функции в точке (3 определения). Свойства функций, непрерывных в точке.
Определение
1:
Функция
непрерывна
в точке
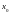 ,
если
,
если
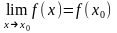 .
.
Определение
2:
Функция
непрерывна
в точке
,
если

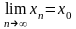 ,
,
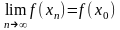 .
.
Определение
3:
Функция
непрерывна
в точке
,
если

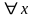
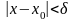
 .
.
Свойства непрерывных функций:
Теорема
1 (локальная огр.): Пусть
функция
непрерывна
в точке
,
тогда
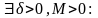
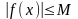 .
.
Теорема
2 (отделимость от 0): Пусть
функция
непрерывна
в точке
и
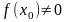 ,
тогда
,
тогда
.
 .
.
Теорема 3 (арифметика непрерывных функций): Пусть , непрерывны в точке , тогда:
1). непрерывна в точке .
2).
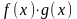 непрерывно в точке
.
непрерывно в точке
.
3).
Если
 ,
то
,
то
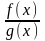 непрерывно
в точке
.
непрерывно
в точке
.
29) Непрерывность сложной функции.
Теорема:
если функция
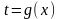 непрерывна
в точке
,
а функция
непрерывна
в точке
,
а функция
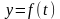 непрерывна
в точке
непрерывна
в точке
 то сложная функция
то сложная функция
 непрерывна в точке
.
непрерывна в точке
.
