9) Свойства сходящихся последовательностей: предельный переход в неравенства.
Теорема: (о предельном переходе в неравенство):
Пусть
,
.
.
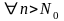
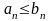Тогда
.
Замечание:
.
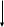
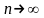
Доказательство (от противного):
Пусть
.
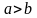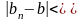
Возьмем
.
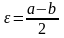Обозначим
.
-
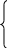
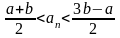
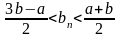
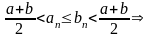
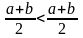противоречие.
Замечание:
Если для элементов последовательности
выполняется
,
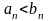то отсюда не следует, что
.
.
=
,
=
,
.
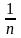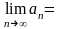
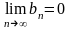Теорема (о промежуточной последовательности).
Пусть
,
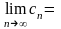и
.
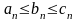Тогда существует
.
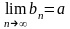Замечание:
( ).
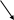
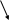
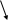
Доказательство:
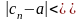
Возьмем произвольный .
.
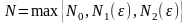Тогда
.
.
(
).
.
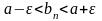Теорема: (об отделимости от нуля).
Пусть
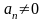и
.
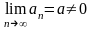Тогда
.
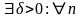
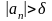Замечание:
-
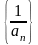ограниченная.
(
).
.
.
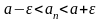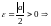
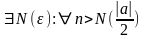
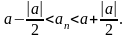
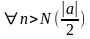
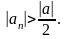
10) Монотонные последовательности. Теорема о пределе монотонной последовательности.
Определение:
-монотонно
возрастающая (монотонно убывающая),
если
(
).
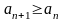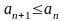Если неравенства строгие, то
последовательности строго возрастающие
(убывающие).
Теорема
(о пределе монотонной последовательности).
Пусть
-монотонно
возрастает и ограничена сверху. Тогда
она сходится, причем
.
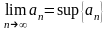Доказательство:
ограничена
сверху =>по теореме существования
точной верхней грани
.
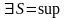Докажем, что
.
:
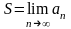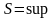1)
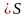
2)
.
Возьмем
произвольный
,
обозначим
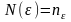из
2).
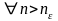1)=>
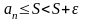
2)=>
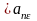(монот.
возр).
Из
этого следует, что
,
=>
.
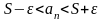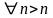
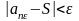Мы доказали достаточное условие числовой сходимости последовательности (монот. и огр.)
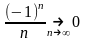(огр.
на б.м.).
11) Число е (доказательство теоремы о существовании предела).
Сложно
доказать, что функция
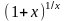при
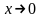имеет предел. Этот предел обозначается
буквой
в
честь открывшего его петербургского
математика Леонарда Эйлера. Установлено,
что это- иррациональное число и что
=2,718281828459….
Формула, определяющая число
по
традиции называется второй замечательный
предел.
.
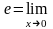Также число
-основание
натуральных логарифмов.
Рассмотрим
.
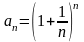1. Ограниченность.
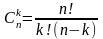-биноминальный
коэффициент.
+
<
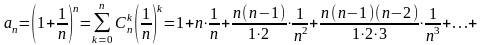
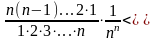
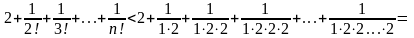
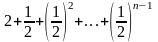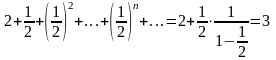
2. Монотонность.
+
.
…
.
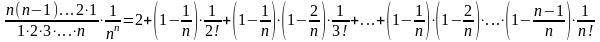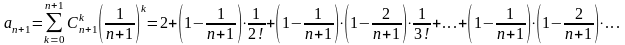
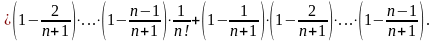
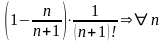По теореме о монотонности последовательности - сходится.
12) Лемма о вложенных отрезках.
Лемма о вложенных отрезках.
Последовательность
отрезков {
}={[
,
]}
наз-ся послед. Вложенных отрезков, если
>
для
любого n.
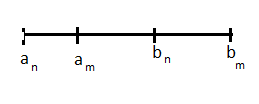
Лемма. { } =={[an,bn]} посл-ть вложенных отрезков, причем {dn} стремится к нулю, где dn=bn-an.
Тогда
существует единственная C
принадлежащая множеству вещественных
чисел, С
для
любого n.
Док-во.
Обозначим A={a1,a2,a3...}-
мн-во левых концов отрезка.
B={b1,b2,b3...}-мн-во
правых концов отрезка, заметим, что
A
.
Док-м
что 
.
1.
=>
=
>
=>
2.
=>
=
>
=>
След-но
A, B
– непустые мн-ва, т.ч.
,
=>
по св-вам действительных чисел 
В
частности при 
=>
, 
.
Д-м,
что C-
единственная точка, принадлежащая
другим отрезкам. Предположим , что 
=>
.
Пусть,
например, 
.
=>
=>
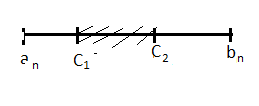->0
=> по св-вам пределов 
,
но 
,
при nстремящемся
к бесконечности =>
=>
=>
=>
C-единственная
точка 
Замечание. Заметим, что С=sup A(inf A).
Д-м,
что C=sup
A 
=>
C-верхняя
грань A.
Нужно док-ть что C-наименьшая верхняя грань A.
Предположим,
что C- не
наименьшая верхняя грань,т. е.
Существует верхняя грань 
:
=>
Повторим
док-во леммы (см. 
И
С) получаемЮ что 
-
получаем противоречие с выбором
,
след-но С наименьшая верхняя грань A,
C=sup
A.Аналогично
док-ся, что C=inf
B.