
- •Ограниченные и неограниченные множества. Примеры.
- •2) Для любого положительного числа в множестве m можно найти число , такое что
- •Арифметика бесконечно малых последовательностей.
- •Доказательство:
- •9) Свойства сходящихся последовательностей: предельный переход в неравенства.
- •13) Подпоследовательности, частичные пределы. Связь предела последовательности с частичными пределами.
- •Доказательство: (метод деления пополам).
- •Доказательство:
- •Доказательство:
Ограниченные и неограниченные множества. Примеры.
Множество
вещественных чисел ![]() называется ограниченным
сверху,
если существует число b,
такое что все элементы X не
превосходят b:
называется ограниченным
сверху,
если существует число b,
такое что все элементы X не
превосходят b:
![]() Множество вещественных
чисел
называется ограниченным
снизу,
если существует число b,
такое что все элементы X не
меньше :b:
Множество вещественных
чисел
называется ограниченным
снизу,
если существует число b,
такое что все элементы X не
меньше :b: ![]()
Множество , ограниченное сверху и снизу, называется ограниченным.
Множество , не являющееся ограниченным, называется неограниченным. Как следует из определения, множество не ограничено тогда и только тогда, когда оно не ограничено сверху или не ограничено снизу.
Примером
ограниченного множества является
отрезок ![]() ,
,
неограниченного —
множество всех целых чисел ![]() ,
,
ограниченного сверху, но неограниченного снизу — луч x < 0,
ограниченного снизу, но неограниченного сверху — луч x > 0.
2) Верхняя и нижняя грани числового множества. Теорема о существовании точной верхней (точной нижней) грани множества //только II определение, эквивалентность не надо.
Точной
верхней гранью
числового множества
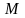 (
(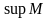 )
называется число
)
называется число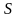 ,
такое что:
,
такое что:
1)
S-
верхняя граница
(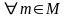
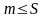 ).
).
2)
Для любого положительного числа
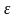 в множестве M
можно найти число
в множестве M
можно найти число
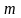 ,
такое что
,
такое что
>
-
.
(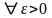
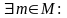 >
-
)
>
-
)
Точной
нижней гранью
числового множества
(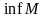 )
называется число
,
такое что:
)
называется число
,
такое что:
1)
S-
нижняя граница
(
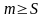 ).
).
2) Для любого положительного числа в множестве m можно найти число , такое что
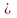 +
.
(
+
)
+
.
(
+
)
Теорема
существования: Пусть
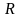 ,
,
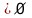 ,
ограниченное сверху (снизу), тогда
существует точная верхняя (нижняя)
грань.
,
ограниченное сверху (снизу), тогда
существует точная верхняя (нижняя)
грань.
Замечание: (аксиома непрерывности множества действительных чисел).
Пусть
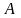 ,
,
и
,
,
и
 ,
,
причем
,
,
причем
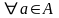 и
и
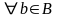 :
:
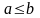 .
Тогда
.
Тогда
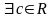 :
:
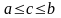 и
.
и
.
, , ограничено сверху.

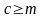
 ,
,
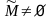 .
.
,
и
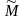 ,
.
,
.
и
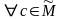
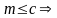
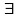
1)
2) > -
Предположим противное:
: .
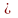 -
-
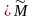 ,
,
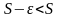 .
Получили
противоречие.
.
Получили
противоречие.
Аналогично для = .
Теорема единственности: Если числовое множество не пусто и ограничено сверху (снизу), то у него есть единственная ( ).
Введем следующие условия:
1)
числовое множество
ограничено
сверху, если можно указать такое число
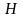 ,
что
для всех чисел
из множества
.
,
что
для всех чисел
из множества
.
2)
числовое множество
ограничено
снизу, если можно указать такое число
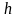 ,
что
для всех чисел
из множества
.
,
что
для всех чисел
из множества
.
Доказательство:
Рассмотрим
множество
,
состоящее из всех чисел
,
таких что для любого числа
из
множества
будет
.
Такие числа
существуют, так как множество
ограничено
сверху. В силу непрерывности множества
действительных чисел существует такое
число
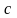 ,
что
,
что
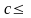 для
любых чисел
(из
)
и
(из
).
для
любых чисел
(из
)
и
(из
).
Покажем,
что
=
.
По определению
,
для всех чисел
из множества
будет
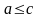 ,
так что первое условие выполнено.
Проверим, что выполнено и второе условие.
Предположим, что оно не выполнено, т.е.
есть такое положительное число
,
так что первое условие выполнено.
Проверим, что выполнено и второе условие.
Предположим, что оно не выполнено, т.е.
есть такое положительное число
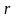 (
>0),
что для всех чисел
из множества
будет
(
>0),
что для всех чисел
из множества
будет
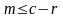 .
Так как
.
Так как
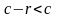 ,
то число
,
то число
 не принадлежит множеству
.
Но это противоречит определению множества
,
которое было множеством всех
чисел
,
таких что для любого числа
из множества
будет
,
а мы нашли число
,
тоже обладающее таким же свойством и
не принадлежащее множеству
.
Полученное противоречие показывает,
что для числа
выполнено
и второе условие из определения верхней
грани.
не принадлежит множеству
.
Но это противоречит определению множества
,
которое было множеством всех
чисел
,
таких что для любого числа
из множества
будет
,
а мы нашли число
,
тоже обладающее таким же свойством и
не принадлежащее множеству
.
Полученное противоречие показывает,
что для числа
выполнено
и второе условие из определения верхней
грани.
3) Числовая последовательность. Предел числовой последовательности. Связь сходящейся и б.м. последовательнсти.
Определение:
функцию
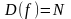 называют
числовой последовательностью.
называют
числовой последовательностью.
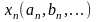 -
члены числовой последовательности.
-
члены числовой последовательности.
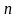 -
номер члена числовой последовательности.
-
номер члена числовой последовательности.
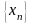 или
или
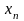 ,
,
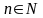
= ,
-общий
член.
,
-общий
член.
Определение:
Число
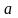 называется пределом последовательности
называется пределом последовательности
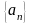 (пишут
(пишут
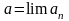 ),
если для любого положительного числа
(
>0)
можно указать такое число
),
если для любого положительного числа
(
>0)
можно указать такое число
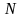 ,
зависящее от
,
что
,
зависящее от
,
что
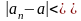 для всех
для всех
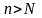 .
.
4) Б.м. последовательности и их свойства.
Определение:
Последовательность
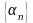 будем
называть бесконечно
малой
последовательностью, если
будем
называть бесконечно
малой
последовательностью, если
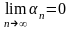 ,
то есть
,
то есть
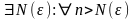
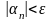 .
.
Теорема:
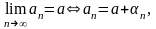
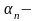 бесконечно
малая последовательность.
бесконечно
малая последовательность.
(I)-
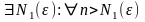
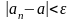
(II)-
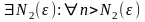
(I)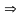 (II)
(II)

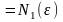
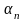 =
=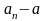
(II)
(I)
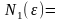
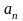 =
=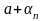
Замечание: Фактически мы дали эквивалентность определений сходящейся последовательности.
