3. Функция вероятности для микроканонического ансамбля.

В основу поиска функции вероятности положим постулат максимума энтропии системы в положении равновесия и вариационный принцип.

Пусть замкнутая дискретная система имеет некоторое равновесное распределение вероятности. Запишем энтропию и условие нормировки, которому подчиняется функция вероятности

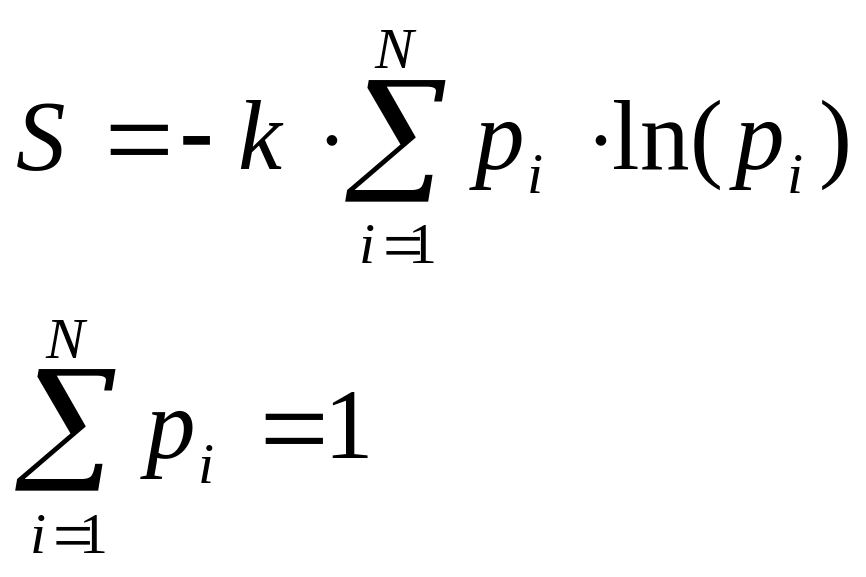. (12) Очевидно, что в положении равновесия вариация энтропии в силу ее экстремальности должна быть равна нулю. Условие нормировки дает дополнительное условие, которому подчиняются вариации вероятностей.

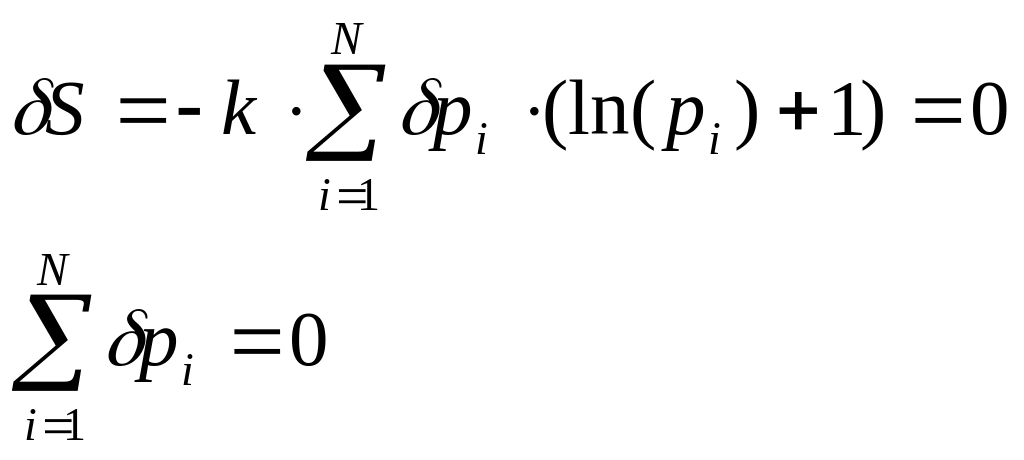. (13) Далее применяем метод неопределенных множителей Лагранжа.¹⁵ Умножаем условие нормировки на некоторый коэффициент  и складываем с вариацией энтропии.

. (14) Метод неопределенных множителей Лагранжа позволяет в полученном выражении все вариации вероятностей формально считать независимыми. Поэтому равенство нулю выражения (14) должно выполняться тождественно. То есть, множители при всех вариациях должны быть равны нулю. Это приводит к уравнению для вероятности

.

Отсюда получаем

. (15) Таким образом, в замкнутой системе все разрешенные состояния имеют одинаковую вероятность (равномерное распределение).

4. Ф ункция вероятности для канонического ансамбля. Статистическая сумма. Связь статистической суммы с термодинамическими величинами.

Рассмотрим систему, помещенную в термостат. Система имеет возможность обмениваться энергией с термостатом. Пусть система имеет дискретный набор состояний с соответствующими вероятностями. К уравнению энтропии и условию нормировки теперь следует дописать формулу средней энергии системы

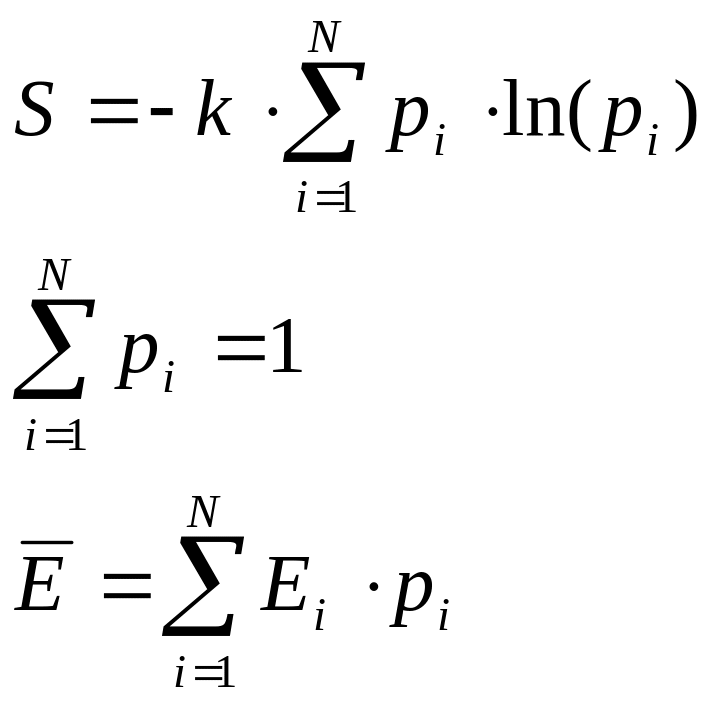. (16) Вычисляем вариацию энтропии и два дополнительных условия, которым подчиняются вариации вероятностей.

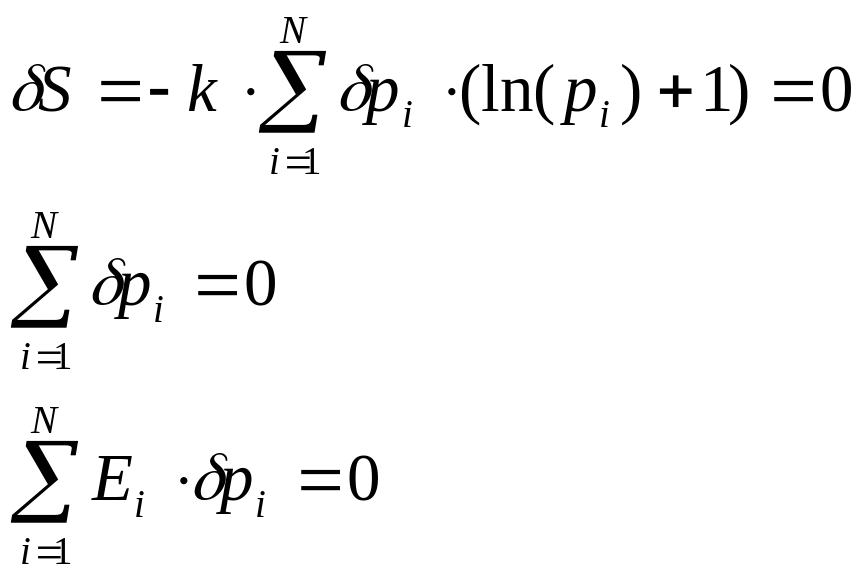. (17) Три уравнения объединяем (складываем) умножая два последних на неопределенные множители Лагранжа  и .

. (18) В этой сумме независимыми являются N – 2 вариаций вероятностей ( и определяются двумя последними уравнениями в (17)). Неопределенные множители  и  выбираем таким образом, чтобы обнулить первые два слагаемых в сумме (18). Остальные слагаемые должны обнуляться в силу тождественности «нулевого» равенства. Таким образом, для определения функции вероятности имеем соотношение

.

Отсюда получаем

.

Константу определяем из условия нормировки функции вероятности

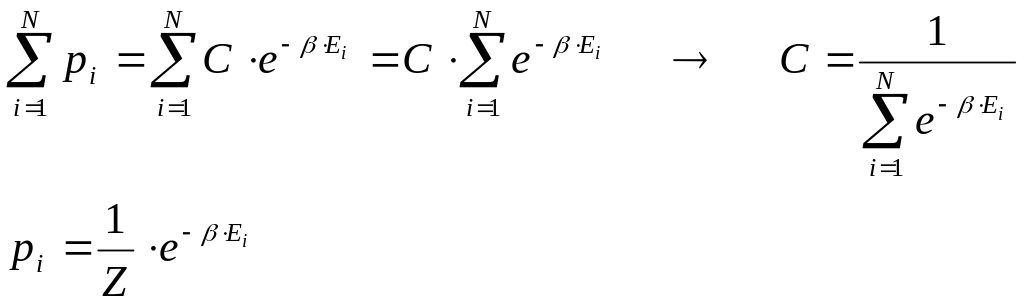. (19) Величину называют статистической суммой канонического ансамбля. В формуле вероятности (19) неизвестным остается неопределенный множитель Лагранжа . Определить его можно методом согласования формул термодинамики и статистической термодинамики.

Вычислим энтропию, используя вероятность (19).

. (20) Сравниваем это выражение с определением свободной энергии Гельмгольца (см. (8))

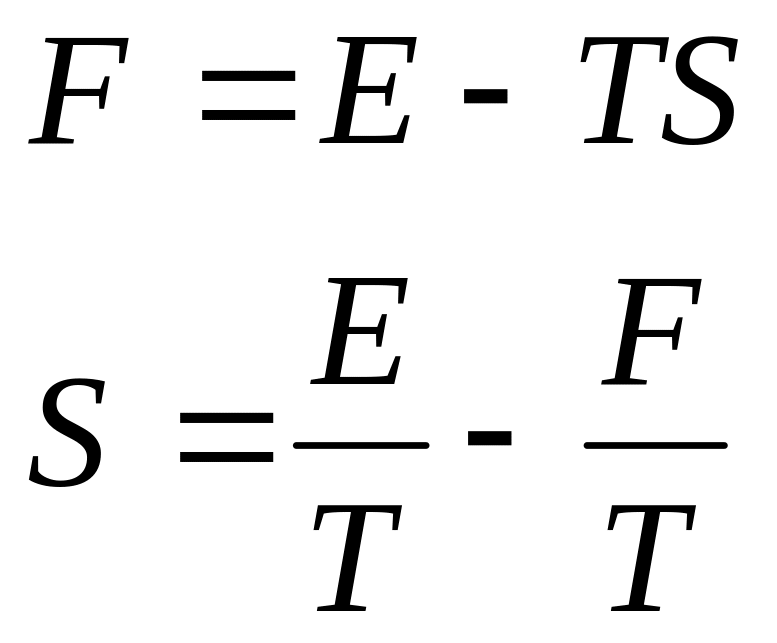. (21) «Совмещая» эти формулы (20 и 21) получаем

, (22) . (23) Окончательно функцию вероятности состояния для канонического ансамбля записываем в виде

. (24) Используя дифференциал свободной энергии (9)

Можно получить формулы, связывающие статистическую сумму с параметрами системы.

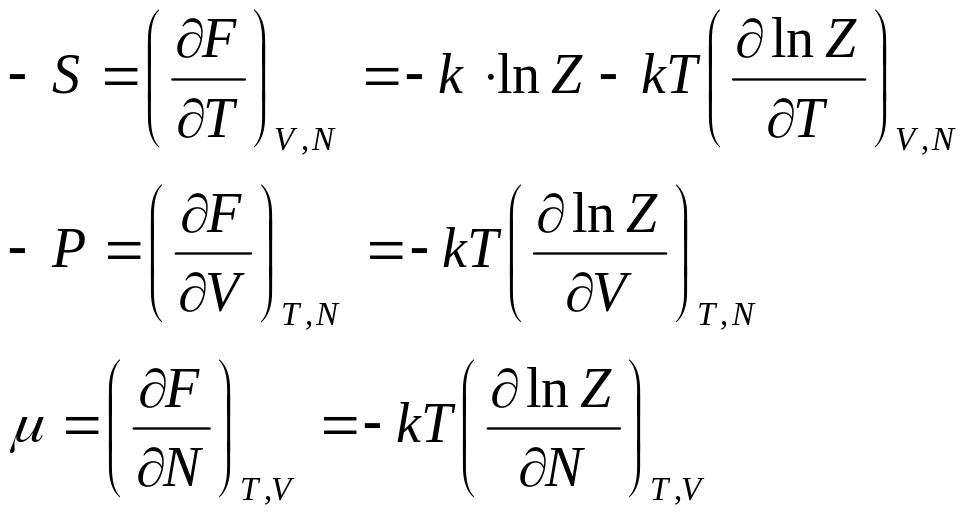. (25) Если умножить первое уравнение на T, то получим формулу (8) для свободной энергии, из которой получаем формулу для энергии системы

. (26)