8. Теплоемкость.

Теплоемкость определяет «температурную инерционность» системы.

.

X - условия теплообмена. Удельные теплоемкости

- массовая удельная теплоемкость

- мольная удельная теплоемкость.¹²

В справочной литературе обычно приводятся значения теплоемкостей при постоянном объеме C_V и постоянном давлении C_P. Величина теплоемкости может быть любой (положительной, отрицательной, нулевой, бесконечной). Величина определяется условиями теплообмена.

 Задача. Определите величину теплоемкости моля идеального одноатомного газа на прямой линии диаграммы P – V.

Уравнение прямой линии в координатах P – V

.

Используемые уравнения (термическое и калорическое уравнения газа, первый закон термодинамики)

.

Из последнего уравнения

.

Производную на прямой линии p₀ – v₀ определяем, используя уравнение прямой и термическое уравнение.

.

. .

График полученного результата показывает диапазон изменения теплоемкости вдоль прямой. В середине линии теплоемкость терпит разрыв. Граничные теплоемкости соответственно равны 5/2 и 3/2. В точке теплоемкость равна 0.

 Задача. Получить уравнение политропического процесса. Политропическим процессом называется процесс при постоянной теплоемкости.

Будем использовать

.

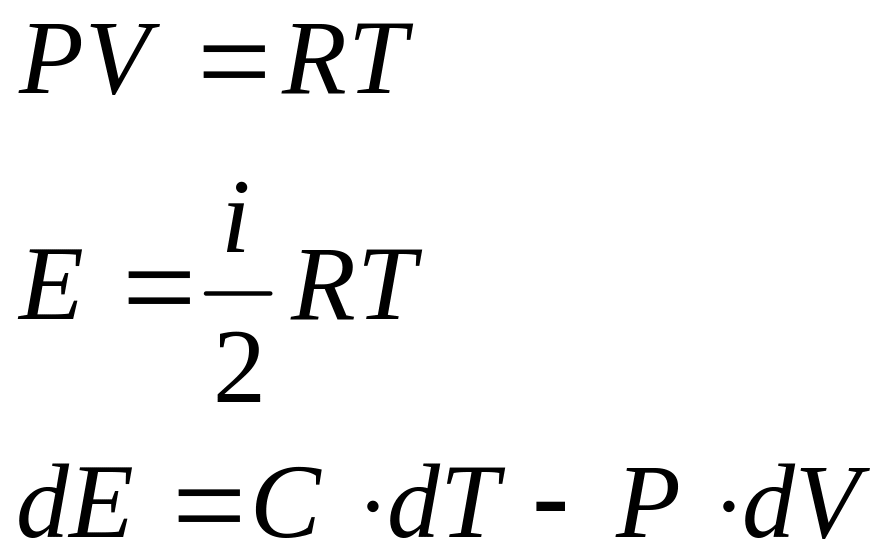Используя первые два уравнения, преобразуем дифференциальное уравнение первого закона термодинамики

.

Обозначим . Дифференциальное уравнение политропы переписывается

. Интегрирование приводит к уравнению

. (10) Здесь и далее теплоемкость выражена в единицах R.

• Изохорный процесс. Очевидно, что в этом случае .

• Изобарный процесс. В формуле (10) перейдем к давлению

.

Очевидно, что давление будет постоянным при условии . Отсюда

.

• Адиабатный процесс. C = 0. Подстановка в (10) определяет уравнение адиабаты

.

• Изотермический процесс. Преобразуем формулу (10) к виду .

Температура будет константой при условии .

• Процесс с линейной зависимостью давления от объема. В формуле (10) избавляемся от температуры

.

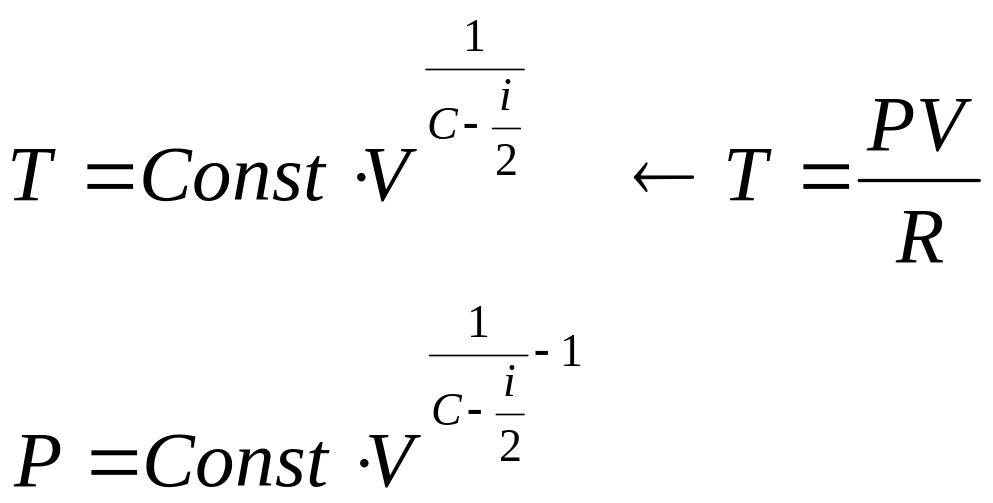Для линейной зависимости давления от объема необходимо выполнения условия

. Отсюда получаем .

Рисунок иллюстрирует спектр политропных процессов с различными теплоемкостями. Процессы идущие вблизи изотермы имеют бесконечные теплоемкости.

2. С татистическая термодинамика.

1. Энтропия. Вероятностная формула энтропии.

Для системы с дискретным набором состояний энтропия определяется в соответствии с формулой¹³

(11) Структура формулы соответствует среднему значению логарифма вероятности. Энтропия обладает свойством аддитивности. Пусть имеем две невзаимодействующие дискретные системы. Тогда вероятность состояния общей системы определяется произведением вероятностей . Энтропия общей системы запишется формулой

.

После преобразования

.

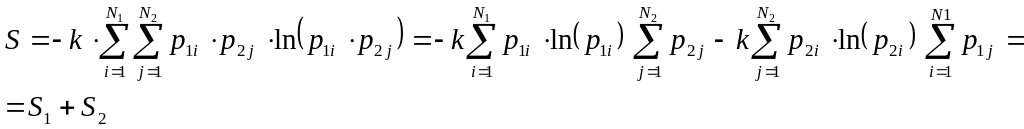Энтропия общей системы равна сумме энтропий ее частей.

2. Термодинамические системы. Классификация по степени изолированности.

   • Полностью изолированная система. Ансамбль изолированных систем называется микроканоническим ансамблем.¹⁴

   • Система, погруженная в термостат (открыта по теплообмену и закрыта по объему и числу частиц) сохраняет постоянную температуру. Ансамбль систем в термостате называется каноническим ансамблем.

   • Система погружена в термостат и открыта по числу частиц. Ансамбль таких систем называется большим каноническим ансамблем.

   • Система, открытая по объему (цилиндр имеет подвижный поршень) сохраняет постоянным давление.

   • Полностью открытая система. Такая система погружена в термостат, имеет подвижный пористый поршень. В ней сохраняется температура, поддерживается постоянным давление и не сохраняется число частиц.