
Прикладная математика 14вар
.docМинистерство образования Республики Беларусь
учреждение образования
Белорусский государственный университет
информатики и радиоэлектроники
Кафедра ПОИТ
Контрольная работа
по предмету:
ПРИКЛАДНАЯ МАТЕМАТИКА
Выполнил: Проверил:
Студент гр. 701022-14 Летохо А. С.
Романюк А.М.
Минск 2009
14 вариант
З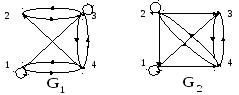 адача № 1.
Для графов G1
и G2
(рис. 14.1)
построить графы G1G2,
G1G2,
G1(G2),
G2(G1),
матрицы смежности вершин А(G1),
А(G2)
и матрицы инцидентности В(G1),
В(G2),
введя предварительно нумерацию дуг. По
матрицам смежности вершин исходных
графов построить матрицы смежности
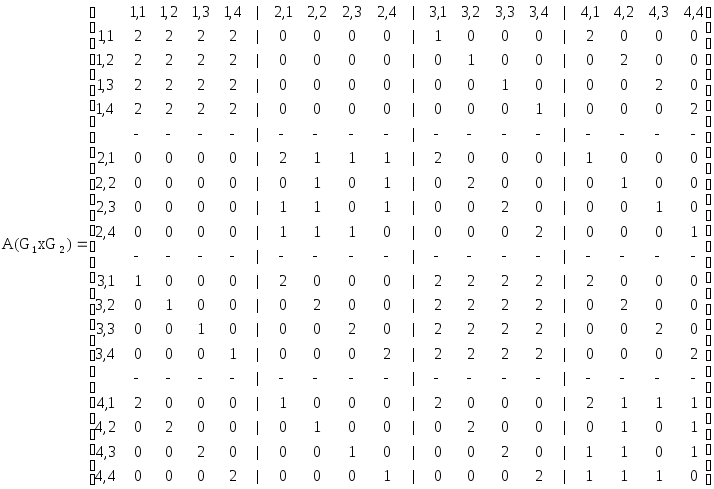
вершин А(G1G2),
А(G1G2),
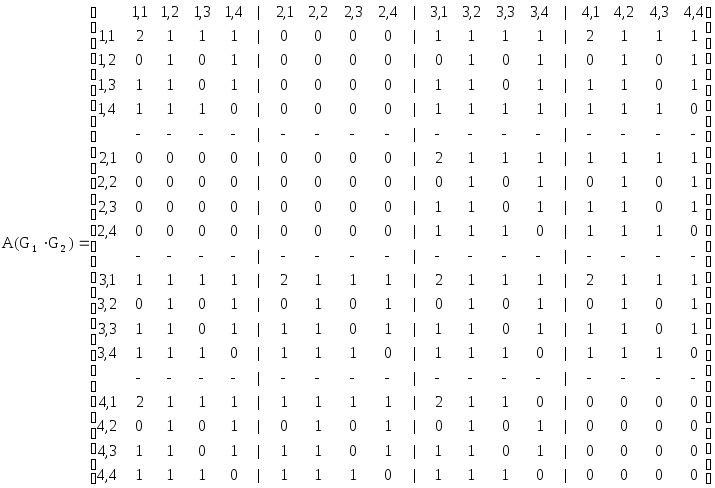
А(G1(G2)),
А(G2(G1)).
Будут ли изоморфны графы G1(G2)
и G2(G1)?
адача № 1.
Для графов G1
и G2
(рис. 14.1)
построить графы G1G2,
G1G2,
G1(G2),
G2(G1),
матрицы смежности вершин А(G1),
А(G2)
и матрицы инцидентности В(G1),
В(G2),
введя предварительно нумерацию дуг. По
матрицам смежности вершин исходных
графов построить матрицы смежности
вершин А(G1G2),
А(G1G2),
А(G1(G2)),
А(G2(G1)).
Будут ли изоморфны графы G1(G2)
и G2(G1)?
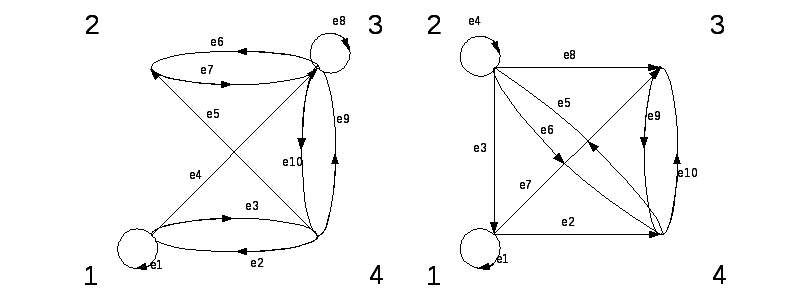
Рис. 14.1
Решение:
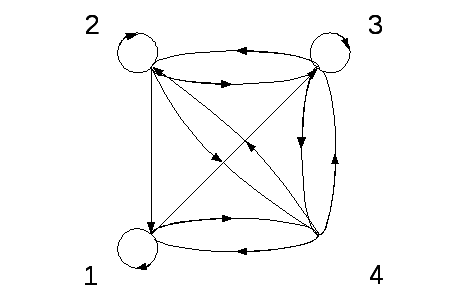
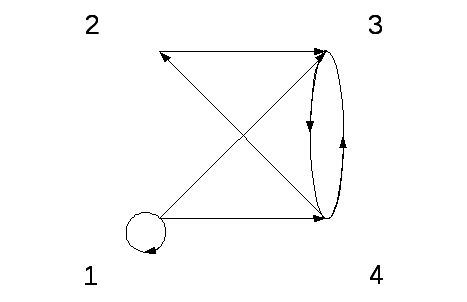
G1G2 G1∩G2

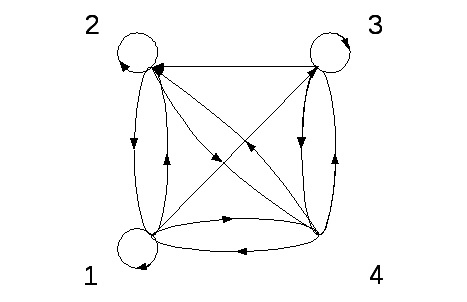
G1(G2) G2(G1)
Таблицы 1.1 и 1.2 для нахождения дуг графов G1(G2) G2(G1) приведены ниже:
Таблица 1.1
|
G1 |
G2 |
G1(G2) |
|
(1, 1) |
(1, 1) (1, 3) (1, 4) |
(1, 1) (1, 3) (1, 4) |
|
(1, 3) |
(3, 4) |
(1, 4) |
|
(1, 4) |
(4, 2) (4, 3) |
(1, 2) (1, 3) |
|
(2, 3) |
(3, 4) |
(2, 4) |
|
(3, 3) |
(3, 4) |
(3, 4) |
|
(3, 4) |
(4, 2) (4, 3) |
(3, 2) (3, 3) |
|
(3, 2) |
(2, 1) (2, 2) (2, 3) (2, 4) |
(3, 1) (3, 2) (3, 3) (3, 4) |
|
(4, 1) |
(1, 1) (1, 3) (1, 4) |
(4, 1) (4, 3) (4, 4) |
|
(4, 2) |
(2, 1) (2, 2) (2, 3) (2, 4) |
(4, 1) (4, 2) (4, 3) (4, 4) |
|
(4, 3) |
(3, 4) |
(4, 4) |
Таблица 1.2
|
G2 |
G1 |
G2(G1) |
|
(1, 1) |
(1, 2) (1, 3) (1, 4) |
(1, 2) (1, 3) (1, 4) |
|
(1, 3) |
(3, 2) (3, 3) (3, 4) |
(1, 2) (1, 3) (1, 4) |
|
(1, 4) |
(4, 1) (4, 2) (4, 3) |
(1, 1) (1, 2) (1, 3) |
|
(2, 1) |
(1, 2) (1, 3) (1, 4) |
(2, 2) (2, 3) (2, 4) |
|
(2, 2) |
(2, 1) (2, 2) (2, 3) (2, 4) |
(2, 1) (2, 2) (2, 3) (2, 4) |
|
(2, 3) |
(3, 2) (3, 3) (3, 4) |
(2, 2) (2, 3) (2, 4) |
|
(2, 4) |
(4, 1) (4, 2) (4, 3) |
(2, 1) (2, 2) (4, 3) |
|
(3, 4) |
(4, 1) (4, 2) (4, 3) |
(4, 1) (4, 2) (4, 3) |
|
(4, 2) |
(2, 1) (2, 2) (2, 3) (2, 4) |
(2, 1) (2, 2) (2, 3) (2, 4) |
|
(4, 3) |
(3, 2) (3, 3) (3, 4) |
(3, 2) (3, 3) (3, 4) |
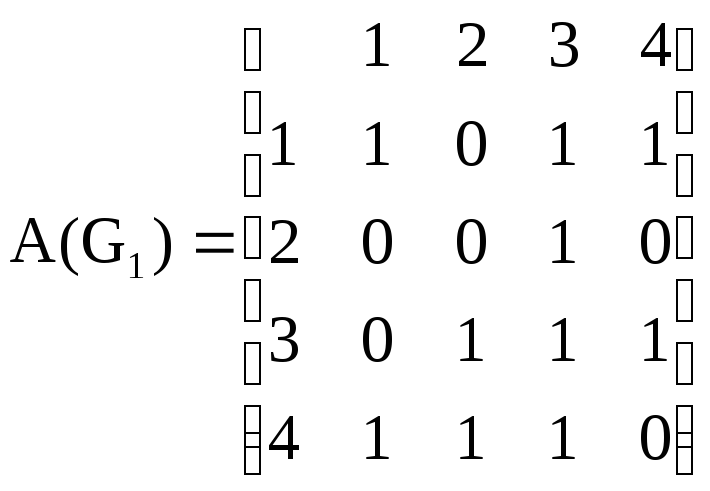


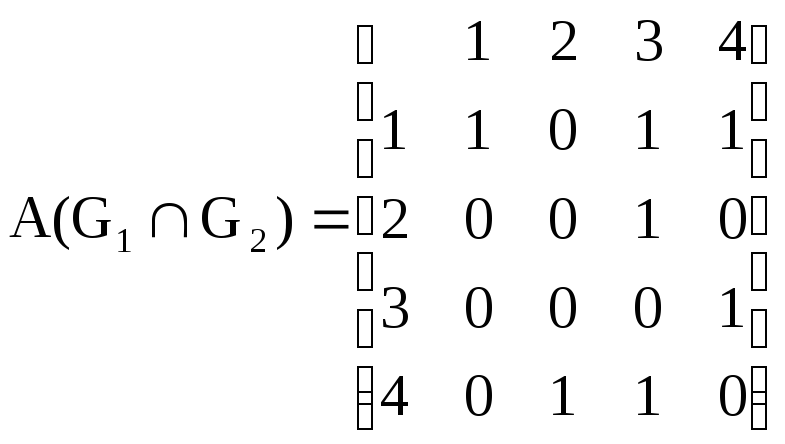
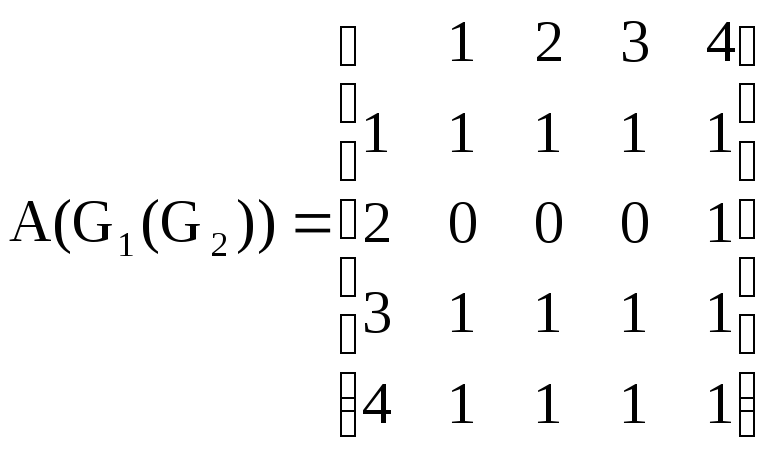
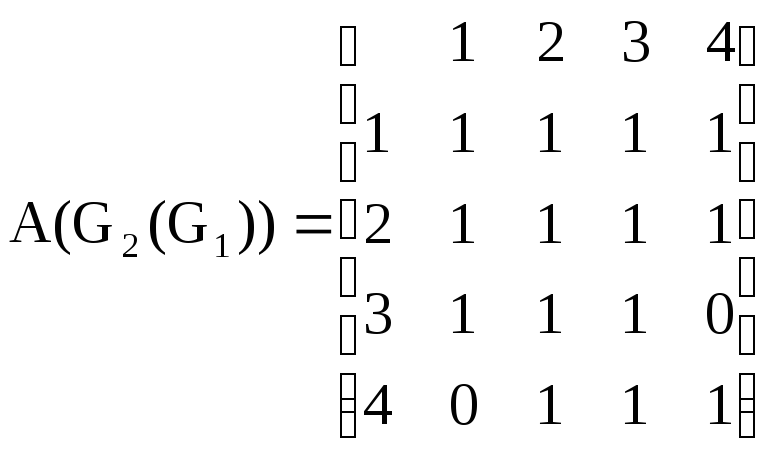
Графы G1(G2) и G2(G1) не изоморфны так как перестановкой строк и столбцов A(G1(G2)) и A(G2(G1)) нельзя добиться их эквивалентности.


З адача № 2.
При условии, что петля считается двойным
ребром, для графов G1
и G2
(рис. 14.2)
построить матрицы смежности вершин
А(G1)
и А(G2),
введя предварительно нумерацию рёбер,
построить матрицы инцидентности В(G1)
и В(G2).
По матрицам смежности вершин исходных
графов построить матрицы смежности
вершин А(G1G2)
и А(G1G2).
адача № 2.
При условии, что петля считается двойным
ребром, для графов G1
и G2
(рис. 14.2)
построить матрицы смежности вершин
А(G1)
и А(G2),
введя предварительно нумерацию рёбер,
построить матрицы инцидентности В(G1)
и В(G2).
По матрицам смежности вершин исходных
графов построить матрицы смежности
вершин А(G1G2)
и А(G1G2).
Рис. 14.2
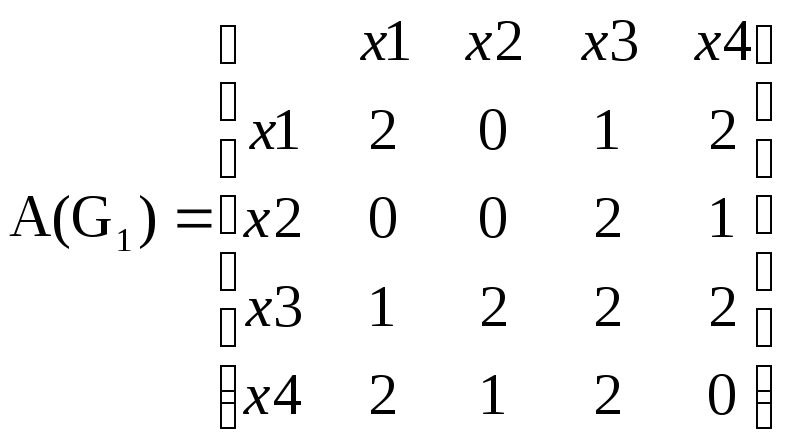
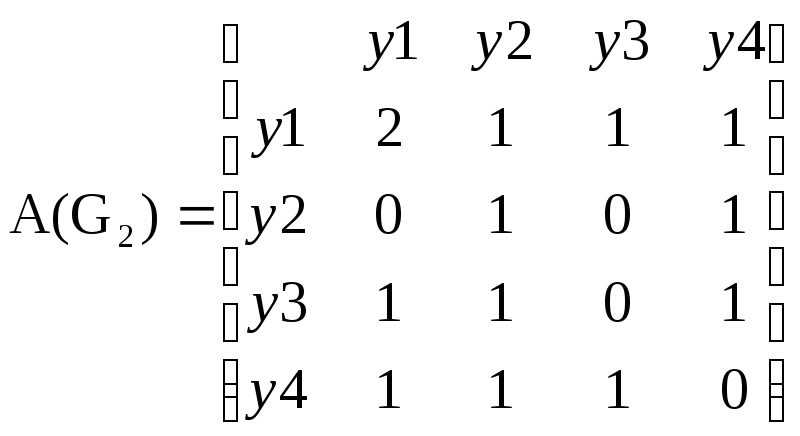


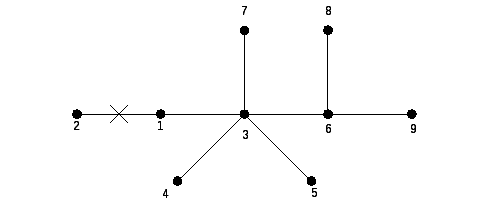
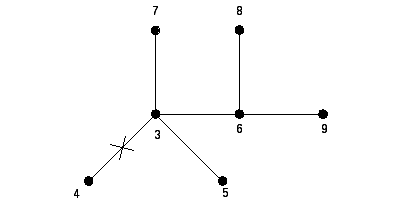
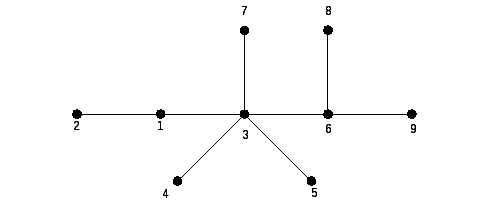
Задача № 3. Построить код (G) по дереву G (рис. 14.3) и восстановить G.
 7
8
7
8
2 1 3 6 9
4 5
Рис. 14.3
Построение
 (1)
(1)
 (1,3)
(1,3)
 (1,3,3)
(1,3,3)
 (1,3,3,3)
(1,3,3,3)
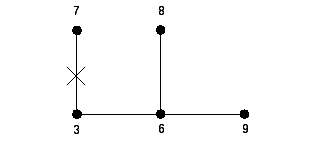 (1,3,3,3,3)
(1,3,3,3,3)
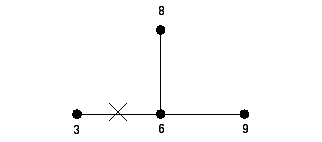 (1,3,3,3,3,6)
(1,3,3,3,3,6)
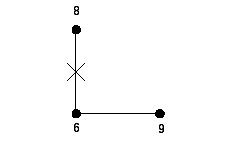 (1,3,3,3,3,6,6)
(1,3,3,3,3,6,6)
Востановление
1333366
123456789
![]()
333366
13456789
![]()
33366
3456789
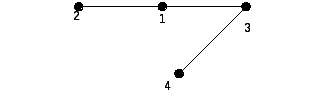
3366
356789
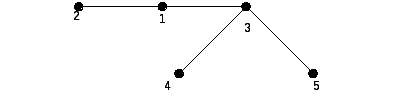
366
36789
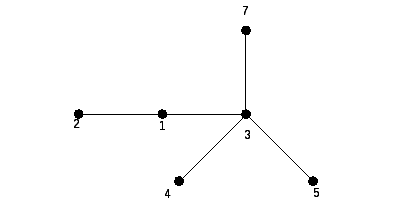
66
3689
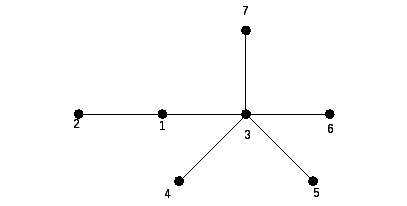
6
689
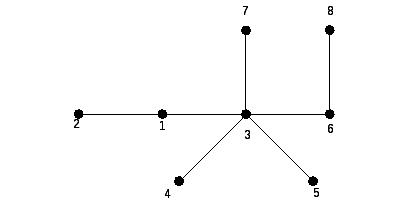
69
Задача № 4. По алгоритму Краскала построить для нагруженного графа G, изображенного на рис. 14.4, минимальный каркас G1 с указанием последовательности выбора рёбер ei. Определить вес построенного каркаса (G1).
 v2
4 v4
v2
4 v4
2 1 8 v3 2 3 3
v1 3 v5 v6
2
7 5 3 6
v9 4 v8 8 v7
4
Рис. 14.4
µ(G1) = 1 + 2 + 2 + 3 + 3 + 3 + 4 = 18
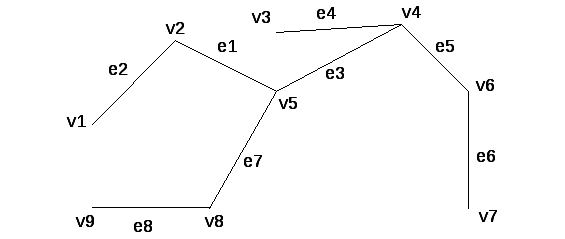
Задача № 5. В графе G, изображённом на рис. 14.5, найти все максимальные внутренне устойчивые множества вершин, наибольшие независимые множества и число внутренней устойчивости (G).
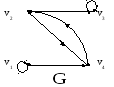
Рис. 14.5
Построим матрицу смежности графа:

Найдем множество внутренней устойчивости методом Магу
1. По единицам матрицы строим парные дизъюнкты:
![]()
2. преобразуем в ДНФ, выполнив все возможные поглощения и операции идемпотентности:
![]()
3. Для полученной конъюнкции выписываем недостающие вершины, образующие множество внутренней устойчивости: {v2},{v4}
Максимальное из таких множеств дает число внутренней устойчивости (здесь число внутренней устойчивости (G)=1)
Найдем множество внешней устойчивости методом Магу:
1. по главной диагонали матрицы смежности проставляем единицы:

2. выписываем построчные дизъюнкции:
![]()
3. Преобразуем в ДНФ, выполняя все возможные поглощения и операции идемпотентности:
![]()
Эти конъюнкции и дают множества внешней устойчивости:
{v1, v2}, { v1, v2, v4}, { v1, v2, v3}, { v1, v2, v3, v4}, { v1, v3, v4}, { v2, v3, v4}, }, {v2, v4}, {v3, v4}, минимальные из них - множества {v1, v2}, {v2, v4} и {v3, v4}.
Задача № 6. Построить максимальный поток и разрез с минимальной пропускной способностью в транспортной сети, приведённой на рис. 14.6, по алгоритму Форда-Фалкерсона.
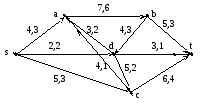
Рис. 14.6
Шаг 0. В сети пропущен поток f величиной ft=5.
Шаг 1. Помечаем узел s пометкой (s+, +).
Шаг 2. Из узла s можно пометить узел c пометкой (s+, 2), из узла c можно пометить узел t пометкой (c+, 2).
Шаг 3. Построен (s, t)-путь, насыщающий поток, {s, c, t}, состоящий из двух прямых дуг. 1=2, 2=2, следовательно, =2. На дугах (s, c) и (c, t) увеличиваем значение потока на 2, тем самым построен новый поток f1 (см. рис. 14.7).
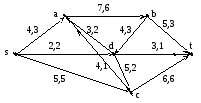
Рис. 14.7
Шаг 1. Помечаем узел a пометкой (s+, +).
Шаг 2. Из узла s можно пометить узел a пометкой (a+, 1), из узла a можно пометить узел b пометкой (a+, 1), и узел t получает пометку (b+, 2).
Шаг 3. Построен (s, t)-путь, насыщающий поток, {s, a, b, t}, состоящий из трёх прямых дуг. 1=1, 2=1, 3=2, следовательно, =1. На дугах (s, a), (a, b), (b, t) увеличиваем значение потока на 1, тем самым построен новый поток f2 (см. рис.14.8).

Рис. 14.8
Шаг 1. Помечаем узел t пометкой (t+, +).
Шаг 2. По рис. 14.11 видно, что узел s помечен быть не может, т.к. на всех дугах, входящих в s, т.е. (s, a), (s, d) (s, c), c(e)=f5(e). Из узла t можно пометить узел b с пометкой (t–, 4) и d с пометкой (t-, 1). Из узла d можно пометить узел a пометкой (d+, 1) и c с пометкой (d+, 3). Для выделения подчеркнём все помеченные и просмотренные узлы.
s
a (d+, 1)
b (t-, 4)
c (d+, 3)
d (t-, 1)
t (t+, +∞)
Таким образом, в
сети построен разрез (Х,
![]() )={(s,
a),
(s,
d)
(s,
c)},
где X={
a,
b,
c,
d,
t},
)={(s,
a),
(s,
d)
(s,
c)},
где X={
a,
b,
c,
d,
t},
![]() ={s},
с пропускной способностью c(X,
={s},
с пропускной способностью c(X,
![]() )
= 4+2+5 = 11 и максимальный поток f5
величиной 11.
)
= 4+2+5 = 11 и максимальный поток f5
величиной 11.
Задача № 7. Доказать справедливость тождества для произвольных множеств А и В:
А\В=(АВ)А.
(АВ)А = ((A∩B)UA)\((A∩B)∩A)
А\В

A∩B

(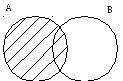 (A∩B)UA)
(A∩B)UA)
((A∩B)∩A)

((A∩B)UA)\((A∩B)∩A)

Откуда видно что (АВ)А = ((A∩B)UA)\((A∩B)∩A) =(АВ)А
Задача № 8. Доказать, что множества Х и Y равномощны, построив взаимно-однозначное соответствие между ними.
Х=[0,1], Y=[10,11]{12}.
Выделим в множестве Y =[10,11]{12} подмножество Y1=[10,11],а в множестве X=[0,1] подмножество X1=[0, 0,5]{1}.
Множество X равномощно подмножеству Y1 так как зависимость между ними Y1=X+10, а множество Y равномощно подмножеству X1 так как Y = 2*X1+10
Согласно теореме 1.5.,если множество А равномощно подмножеству В1 множества В, а множество В равномощно подмножеству А1 множества А, то множества А и В равномощны, множества X Y – равномощны.
Задача № 9. Даны три вещественных функции:
f(x)= –3х4+6, g(x)= –5x+12, h(x)=7x+29.
1) Найти заданные композиции функций: fgh, hgf, hff.
2) Являются ли f, g, h инъекциями, сюръекциями, биекциями на R?
3) Найти обратные функции к f, g, h. Если функции со своими областями определения обратных не имеют, то найти обратные функции к их сужениям.
1) D(f)=D(g)=D(h)=R, поэтому все три указанные композиции функций определены на R.
fgh(x)=f(gh(x))=-3(gh(x))4+6=-3(-5h(x)+12)+2)4+6=-3(-5(7x+29)+2)4+6
hgf(x)=h(gf(x))= 7gf(x)+29 =7-5f(x)+12+29=7-5f(x)+12+29
hff(x)= 7ff(x)+29=7-3f(x)4+6+29 =7-3(-3x4+6)4+6+29.
2) Рассмотрим
функцию f(x)=-3x4+6.
Производная функции
![]() =-12x3
не является
больше 0 на интервале (-;+∞).
Поэтому f
не инъективна.
=-12x3
не является
больше 0 на интервале (-;+∞).
Поэтому f
не инъективна.
Функция f по теореме 3.2 не является сюръекцией на R. Итак, f: RR – не биекция.
Рассмотрим функцию
g(x)=-5x+12.
Производная функции g
:![]() для любого xR},
поэтому g
является строго убывающей функцией на
(–,+).
Поэтому f
инъективна
Итак, g:
RR
является
биекцией.
для любого xR},
поэтому g
является строго убывающей функцией на
(–,+).
Поэтому f
инъективна
Итак, g:
RR
является
биекцией.
Рассмотрим функцию
f(x)=2x9–7.
Производная функции
![]() =18x8>0
для всех xR\{0},
поэтому f
является строго возрастающей функцией
на (–,0)(0,+).
=18x8>0
для всех xR\{0},
поэтому f
является строго возрастающей функцией
на (–,0)(0,+).
![]() =0,
f(0)= –7f()
для 0.
Поэтому f
инъективна.
=0,
f(0)= –7f()
для 0.
Поэтому f
инъективна.
Функция f
непрерывна на R.
![]() и
и
![]() .
Поэтому f
является сюръекцией на R.
Итак, f:
RR
– биекция.
.
Поэтому f
является сюръекцией на R.
Итак, f:
RR
– биекция.
Рассмотрим функцию
h(x)=![]() .
Производная функции h
:
.
Производная функции h
:![]() для xR,
следовательно, h(x)
строго возрастает на R,
значит, h(x)
– инъекция. 0<7x<+
для всех xR,
, -29<
для xR,
следовательно, h(x)
строго возрастает на R,
значит, h(x)
– инъекция. 0<7x<+
для всех xR,
, -29<![]() <+
для всех xR.
Значит, h
не является сюръекцией на R.
Итак, h:
RR
не является
биекцией.
<+
для всех xR.
Значит, h
не является сюръекцией на R.
Итак, h:
RR
не является
биекцией.
3) Поскольку f не инъекция то найдём обратную функцию к сужению:
–3х4+6 =y
–3х4=y-6
х4 =(-y/3)+2
![]()
Итак,
![]() ,
xR.
,
xR.
Поскольку g: RR – биекция, то по теореме 3.1 на R существует обратная функция к g – g –1: RR.
–5x+12=y
–5x=y-12
x=-0.2y+2.4
Итак,
![]() .
.
Е(h)=(–29;+). Поскольку h – инъекция на R, то h: RE(h) – биекция. Тогда по теореме 3.1 для функции h существует обратная функция h –1: E(h)R.
5x+29=y;
5x=(y-29);
x=log7(y-29).
Итак, h –1(x)=log7(x-29), x(–29;+).
Задача № 10. Является ли транзитивным бинарное отношение R1R2, если отношения R1 и R2 транзитивны? В случае отрицательного ответа необходимо привести конкретный пример.
Не является. Покажем это на примере:
Для транзитивного R1 для параллельных прямых a1 b1 c1 : a1||b1 b1||c1 то и a1||c1.
Для транзитивного R2 для параллельных прямых a2 b2 c2 : a2||b2 b2||c2 то и a2||c2.
Для R1R2 в общем случае не являются параллельными a1 a2 ,b1 b2, c1 c2 , a1 b2 и т. д.
