
Матан(ответы,)
.docxНеобходимый минимум определений и утверждений
Отображение (функция).
Пусть имеются 2 множества Х и У. Говорят, что имеется функция, определенная на Х, если в силу некоторого закона(правила) f каждому элементу х из Х соответствует элемент у из У
Взаимообратное отображение (биективное отображение).
f(X)=Y(сюръективность)
Если для любых х1 и х2 из Х f(x1)=f(x2) следует, что х1=х2. То есть различные элементы имеют различные образы. (инъективность)
f(x)=y, то f-1(y)=x
Равномощные множества.
Это множества, между которыми можно установить взаимооднозначное соответствие.
Счетные и несчетные множества.
Всякое множество, эквивалентное множеству натуральных чисел называется счетным. Если бесконечное множество неэквивалентно множеству натуральных чисел, то оно называется бесконечным.
Верхняя (нижняя) грань.
Не пустое множество А из R называется ограниченным сверху, если существует число b из R, такое, что для любого а из R a<=b. b называют верхней гранью.
Принцип вложенных отрезков.
Пусть М – система вложенных отрезков, тогда существует ч такой, что для любого I из М все отрезки из М имеют общую точку.
Предел числовой последовательности.
Число А называется пределом числовой последовательности {Xn}, если для любого E(эпсилон)>0 найдется такой номер, начиная с которого выполняется неравенство |Xn-A|<E.
Критерий Вейерштрасса сходимости числовой последовательности.
Пусть {Xn}-неубывающая(невозрастающая) последовательность. Тогда Хn сходится тогда и только тогда Хn ограничена сверху(снизу).
Число e.
e =
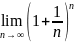
Лемма Больцано-Вейерштрасса.
Любая ограниченная последовательность содержит сходящуюся подпоследовательность.
Критерий Коши сходимости числовой последовательности.
{Xn} сходится ↔ для любого Е>0 существует N такое что для любого n>N для любого n’>N
|xn-xn’|<E
Верхний и нижний пределы числовой последовательности.
Число α(конечное, +∞ или -∞) называется верхним (нижним) пределом последовательности {Xn}, если существует подпоследовательность {Xnk}, сходящийся к нему и при этом всякая другая подпоследовательность последовательности {Xn} сходится к числу не большему(не меньшему) чем α.
Элементарные функции (определение, графики).
Целая и дробные рациональные функции.
Степенная функция.
Показательная функция.
Логарифмическая функция.
Тригонометрические функции.
Обратные тригонометрические функции.
(написать все возможные функции каждого вида и построить графики)
Предел функции.
Говорят, что функция f(x) имеет предел, конечный или нет, при xa, если какую бы последовательность с пределом а, извлеченную из Х, не пробегала независимая переменная х, соответствующая последовательность значений функций f(x1),f(x2)…f(xn)… всегда имела предел А.
Критерий Коши существования предела функции.
Функция f(x) имеет пределом число А при xa, если для каждой δ>0 |f(x)-A|<E лишь только |x-a|<δ.
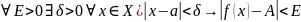
Два замечательных предела.
1ой замечательный предел:
 =1
=1
2ой замечательный предел:
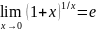
Понятие непрерывности функции в точке.
-Функция f(x) называется непрерывной в точке х=х 0
Если
 =f(x0).
=f(x0).
Если это соотношение не выполняется, то в этой точке функция имеет разрыв.
- Функция f(x) называется непрерывной в точке х=х 0
Если бесконечно малому приращению аргумента соответствует бесконечно малое при ращение функции.
Классификация точек разрыва.
Точка разрыва х0 называется точкой разрыва 1ого рода, если существуют конечные, односторонние пределы f(x-0) и f(x+0). Если один из указанных пределов не существует, то точка разрыва называется точкой разрыва 2ого рода.
Теорема Вейерштрасса о максимальном значении.
Если функция f(x) непрерывна на отрезке с то:
Она ограничена, то есть существует конечное m и M, такое, что m≤f(x)≤M, при a≤x≤b.
f(x) достигает на этом отрезке точных верхней и нижней границ, то есть точка, где функция принимает максимальное значение и есть точка, где функция принимает минимальное значение.
Равномерная непрерывность.
Функция f(x)
называется равномерно непрерывной на
Х, если
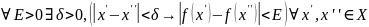 .
.
Теорема Кантора о равномерной непрерывности.
Пусть f(x) непрерывна на [a,b], тогда f(x)-равномерно непрерывна на [a,b].
Дифференцируемость функции в точке.
Говорят, что функция f(x) дифференцируема в точке x0,
Если:
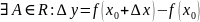
Модно представить в виде:
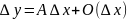
Производная в точке, дифференциал.
Если существует
предел отношения приращения функции
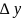 к вызвавшему его приращению независимой
переменной
к вызвавшему его приращению независимой
переменной
 х
при
х
при
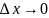 :
:

То он называется производной f(x) по независимой переменной х в точке х=х0
Дифференциалом
функции f(x)
называется выражение 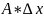 =dy=df
=dy=df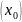 (из
предыдущего определения)
(из
предыдущего определения)
Геометрический смысл производной и дифференциала.
Геометрический смысл производной
y’(x)=tgα, где α-это угол между касательной к графику y(x) и положительным направление оси OX.
Геометрический смысл дифференциала.
Дифференциал dy есть приращение ординаты касательной.
Таблица производных.
Дифференцирование композиции функций.
Производные арифметических операций.
Требуется дифференцируемость функций f(x) и g(x) в точке х. Тогда:
1) (с*f(x))’=c*f’(x), c=const.
2) (f(x)+(-)g(x))’=f’(x)+(-)g’(x)
3) (f(x)*g(x))’=f’(x)g(x)+f(x)g’(x)
4)
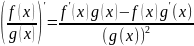
Производная сложной функции:
Пусть:
1)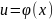 имеет в точке
производную
имеет в точке
производную
2) y=f(u)
имеет в соответствующей точке
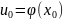 производную, тогда сложная функция
y=f(
производную, тогда сложная функция
y=f(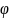 (x))
также имеет сложную производную и:
(x))
также имеет сложную производную и:

Или:
yx’=yu’* ux’
Дифференцирование обратной функции.
Пусть
1)f(x) и g(y) взаимно обратные функции
2) f(x) и g(y) непрерывны в точке х0 и y0=f(х0)
3) f(x) в точке х0 имеет производную не равную нулю
Тогда в точке y0 функция g(y) имеет производную равную g’(y0)=1/f ' (х0)
Производные высших порядков (формула Лейбница).
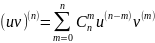
Теорема Ферма.
Пусть функция f(x) определена в некотором промежутке Х и во внутренней точке С принимает наибольшее (наименьшее) значение. Если в этой точке существует конечная производная f'(c) то f’(c)=0.
Теорема Ролля.
Пусть
f(x) – непрерывна на отрезвке АВ
существует конечная производная f'(x) во всех точках на интервал (а,b)
f(a)=f(b)
тогда существует точка С из (a,b) такое что f’(c)=0.
Теорема Лагранжа.
Пусть
1)f(x)-непрерывна на [a,b]
2) существует
производная в каждой точке интервала
(a,b),
существует точка С из (a,b)
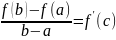
Теорема Коши.
1)Пусть f(x) и g(x) непрерывны на [a,b],
2)Существует производная f'(x) и g’(x) на интервале (a,b)
3)g’!=0 на (a,b)
Тогда существует точка С из (a,b) такая что:

Формула Тейлора с формами Лагранжа и Пеано остаточного члена.
Лагранжа
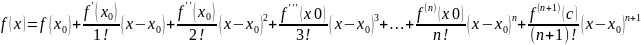
Пеано

Применение дифференциального исчисления к исследованию функций: монотонность, экстремумы, выпуклость.
Утв.: Пусть f(x) дифференцируема на (a,b), тогда если:
f’(x)>0
ф-ия возрастает
f’(x)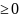
f’(x)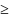 0
ф-ия не убывает
f’(x)
0
ф-ия не убывает
f’(x)
f’(x) =0
ф-ия
f(x)=const
f’(x)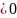
f’(x) 0
ф-ия не возрастает
f’(x)
0
ф-ия не возрастает
f’(x)
f’(x)>0 ф-ия убывает f’(x)
Опр.: Ф-ия f(x)
имеет максимум(минимум) (экстремум
ф-ии), если
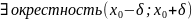 такая, что
такая, что
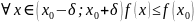 (
(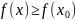 )
)
Теорема 1: Пусть в
окрестности
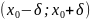 точки
точки

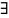 конечная производная ф-ии f(x)
и справа от
,
и слева от
производная сохраняет определенный
знак
конечная производная ф-ии f(x)
и справа от
,
и слева от
производная сохраняет определенный
знак
Если f’(x) при переходе ч/з меняет знак «+» на «-», то точка явл-ся точкой строгого максимума
Если f’(x) при переходе ч/з меняет знак «-» на «+», то точка явл-ся точкой строгого минимума
Если f’(x) при переходе ч/з не меняет знак, то экстремума нет
Теорема 2: Пусть f(x) имеет производную f ’(x) в окрестности точки и производную f ”(x) в точке и f ’( )=0.
Если f ”( )>0, то - точка минимума
Если f ”( )<0, то - точка максимума
Теорема 3: Пусть ф-ия f(x) имеет в точке производный до порядка n включительно. Если
f
’(
)=f
”(
)=…=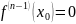 и
и
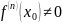 ,
то при нечетном n
в точке
нет
экстремума, а при четном n
точка
явл-ся точкой экстремума, причем если
,
то при нечетном n
в точке
нет
экстремума, а при четном n
точка
явл-ся точкой экстремума, причем если
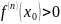 - точка минимума
- точка минимума
если
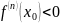 – точка максимума
– точка максимума
Опр.: График ф-ии наз-ся выпуклым вверх (вниз) в точке , если окрестность точки такая, что для всех точек этой окрестности касательная к кривой в точке расположена выше (ниже) кривой.
Опр.: Ф-ия выпукла вверх (вниз) на [a,b], если каждая дуга графика этой ф-ии лежит не ниже (не выше) стягивающей ее хорды.
Опр.: Точка перегиба – точка графика дифференцируемой ф-ии, при переходе ч/з которую график меняет выпуклость вверх на выпуклость вниз или наоборот.
Теорема 4: Если 2ая производная ф-ии y=f(x) положительна (отрицательна) на (a,b), то график этой ф-ии явл-ся выпуклым вниз (вверх) на этом интервале.
Теорема 5: Если 2ая
производная ф-ии y=f(x)
обращается в точке
в 0 и при переходе ч/з эту точку меняет
знак, то точка (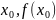 )
графика данной ф-ии явл-ся точкой
перегиба.
)
графика данной ф-ии явл-ся точкой
перегиба.
Правило Лопиталя. Раскрытие неопределенностей.
I. Пусть
1)f(x) и g(x) определены на (a,b)
2)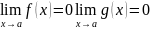
3) На [a,b] существует конечная производная f’(x) и g’(x) при чем g’(x)!=0
4)существует конечный или нет
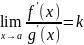
Тогда
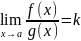
II. Пусть
1)f(x) и g(x) определены на [c,+∞)
2)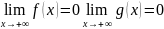
3) На [c,+∞) существует конечная производная f’(x) и g’(x) при чем g’(x)!=0
4)существует конечный или нет
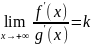
Тогда
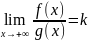
III. Пусть
1)f(x) и g(x) определены на [a,b],
2)
3) На [a,b] существует конечная производная f’(x) и g’(x) при чем g’(x)!=0
4)существует конечный или нет
Тогда
Открытые и замкнутые множества.
Множество, целиком состоящее из внутренних точек, называется открытым.
Множество называется открытым, если оно содержит каждую точку вместе с Е (эпсилон) окрестностью.
Понятие предела функции многих переменных.
Функция
 имеет пределом число A,
при ММ0(
имеет пределом число A,
при ММ0(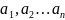 ),
если для:
),
если для:
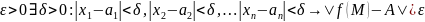
Двойные и повторные пределы.
Дифференцируемость функции многих переменных.
Дифференциал функции многих переменных.
Частные производные функции многих переменных.
Частная производная функции f(x,y,z) в точке (x0,y0,z0) называется
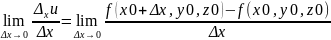
Производная по направлению.
Если с каждой точкой М, определенной пространственной области, связана некоторая скалярная или векторная величина, то говорят, что задано поле этой величины, соответствующее скалярное или векторное.
Пусть l-направленная прямая, Мо принадлежит l фиксированная точка. М принадлежит l-движется. Будем считать величину направленного отрезка МоМ>0, если направление МоМ совпадает с направлением оси l и <0 иначе.
Производной функции V(M) в точке Мо по направлению l называется предел:
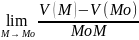
Градиент функции.
Если V(M)-скалярное поле, то вектор
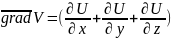 -называется
градиентом поля.
-называется
градиентом поля.
Формула Тейлора функции многих переменных.
Рассмотрим ф-ию
2х переменных, которые в окрестности
точки (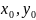 )
имеет непрерывные производные до n+1го
порядка. Придадим
)
имеет непрерывные производные до n+1го
порядка. Придадим
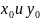 приращения
приращения
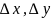 соответственно.
соответственно.
Утв.:
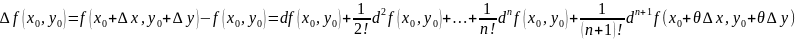 (0<
(0<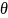 <1),
где дифференциалы dx
и dy
равны
<1),
где дифференциалы dx
и dy
равны
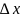 и
.
и
.
Необходимое условие экстремума функции многих переменных.
Пусть функция
u=f(x1,x2…xn)
в точке (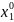 ,
,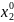 …
…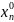 )
имеется экстремум. Если в этой точке
существуют конечные и частные производные,
то они равны 0.
)
имеется экстремум. Если в этой точке
существуют конечные и частные производные,
то они равны 0.
Достаточное условие экстремума функции многих переменных.
Пусть (х0,y0)-стационарная точка
1)если a11*a22- >0,
то в точке (х0,y0) функция f(x,y)
имеет экстремум. При чем это максимум
при а11<0 и минимум при а11>0.
>0,
то в точке (х0,y0) функция f(x,y)
имеет экстремум. При чем это максимум
при а11<0 и минимум при а11>0.
2) Если
a11*a22-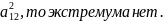
Первообразная. Неопределенный интеграл.
F(x)-первообразная от функции f(x) на промежутке Х, если на Х F’(x)=f(x) (dF=f(x)dx)
Выражение F(x)+C, где F(x)-первообразная от функции f(x) и С произвольная постоянная называется неопределенным интегралом от функции f(x).
Таблица неопределенных интегралов.
Замена переменных в неопределенном интеграле.
Если
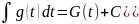 ,
,
то
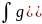
Интегрирование по частям в неопределенном интеграле.
Пусть u=u(x), v=v(x)- непрерывные, дифференцируемые функции, тогда:
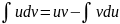
Интегральная сумма.
Рассмотрим задачу определения площади криволинейной трапеции. Разобьем отрезок [a,b] точками a=x0<x1<…<xn=b
Пусть
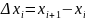
Площадь i-того
прямоугольника yi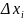 =f(
=f(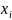 )
)
Тогда приближенное значение площади
S
S=lim
Определенный интеграл Римана.
Число I называется определенным интегралом Римана. если для любого Е>0 существует δ>0 такая что для любого разбиения с |λ| <δ и для любого выбора точек c|I-σ|<E, где:

Необходимое условие интегрируемости (определенный интеграл).
Пусть f(x) интегрируема на [a,b], тогда она ограничена на [a,b].
Достаточное условие интегрируемости (определенный интеграл).
Для существования определенного интеграла необходимо и достаточно, чтобы было:
 ,
,
Где
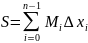
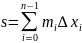

Первая теорема о среднем.
Пусть:
g(x) и f(x) интегрируемы на [a,b],
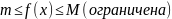
g(x) не меняет знак на [a,b],
тогда:
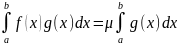 ,
,
Где:
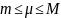
Если
при это f(x)
непрерывна, то
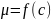 ,
где с из[a,b].
,
где с из[a,b].
Вторая теорема о среднем.
Пусть:
1)g(x) и f(x) интегрируемы на [a,b]
2) g(x) монотонна на [a,b]
Тогда:
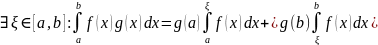
Формула Ньютона-Лейбница.
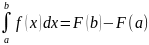
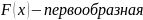
Интегрирование по частям в определенном интеграле.
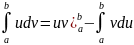
Замена переменных в определенном интеграле.
Пусть
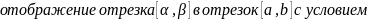
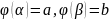 .
.
Пусть на
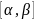 существует непрерывная производная
существует непрерывная производная
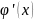 ,
тогда для любой непрерывной функции
f(x) верна формула:
,
тогда для любой непрерывной функции
f(x) верна формула:
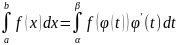
Длина кривой. Вычисление длины кривой.
Несобственный интеграл Римана.
Критерий Коши сходимости несобственного интеграла.
Для сходимости несобственного интеграла:
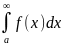
Необходимо и достаточно, чтобы:
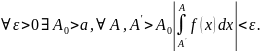
Абсолютная (условная) сходимость несобственного интеграла.
Если интеграл сходится абсолютно, то он сходится.
Если интеграл сходится, но не абсолютно, то его называют условно сходящимся.
Интеграл:
Называется абсолютно сходящимся, если сходится интеграл:
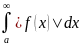
Теорема сравнения (несобственный интеграл).
Если существует
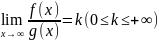 и f(x)
и f(x)
То из сходимости
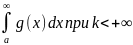
а из расходимости 1ого интеграла при k>0 следует расходимость 2ого.
При 0<k< оба интеграла сходятся или расходятся
одновременно.
оба интеграла сходятся или расходятся
одновременно.
Признак Абеля-Дирихле сходимости интеграла.
Пусть f,g
определены на [a,
]
и интегрируемы на [a,A]
для любого А>а . Тогда
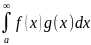 сходится, если выполняется:
сходится, если выполняется:
Либо пара условий
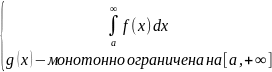
Либо пара условий:
Ф(b)= -ограничена
g(x)-монотонна стремится к нулю при x
Числовой ряд. Сходимость числового ряда.
Пусть дана числовая последовательность:

Их сумма называется числовым рядом, а числа членами ряда:

Если последовательность {Sn} имеет конечный или бесконечный предел S, то он называется суммой ряда. Если эта сумма конечна, то ряд называется сходящимся.
Теоремы сравнения.
Теорема сравнения 1.
Пусть даны 2 положительных ряда:
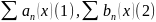
Если, начиная с некоторого номера N для всех n>N выполнено:
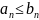
То из сходимости ряда (1) следует сходимость ряда (2), а из расходимости (1) следует расходимость (2).
Теорема сравнения 2.
Пусть
ряды (1) и (2) положительные и для любого
n
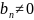 .
Пусть существует предел:
.
Пусть существует предел:
 )
)
Если
ряд (2) сходится к k<
,
то сходится (1). Если (2) расходится и k>0,
то ряд (1) расходится(если
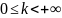 то оба ряда расходятся или сходятся
одновременно)
то оба ряда расходятся или сходятся
одновременно)
Теорема сравнения 3.
Пусть (1) и (2)
положительные ряды и для любого n
,
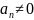 .
Пусть, начиная с некоторого N выполнено:
.
Пусть, начиная с некоторого N выполнено:
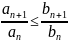
Тогда из сходимости (2) следует сходимость (1).
Признаки сходимости положительных рядов: Коши, Даламбера, Раабе, интегральный признак Коши.
Коши:
Пусть существует предел:
