5. Расчет сплошной колонны

Данные для проектирования

Бетон колонны класса В40 с расчетными характеристиками при коэффициенте условий работы γ_b2 = 1; R_b = 22 МПа; R_bt = 1,40 мПа; E_b = 36∙10³ МПа.

Продольная арматура класса A400 (R_s = R_sc = 355 МПа); E_s = 2∙10⁵ МПа; α_s = E_s / E_b = 2∙10⁵/32,5∙10³ =6,15); поперечная арматура класса А240.

5.1 Расчет надкрановой части колонны

Размеры прямоугольного сечения b = 400 мм; h = h₁ = 600 мм; для продольной арматуры принимаем a = a^' = 40 мм, тогда рабочая высота сечения h₀ = h - a = 600 - 40 = 560 мм.

Рассматриваем сечение II-II на уровне верха консоли, в которой действуют три комбинации расчетных усилий.

Комбинации усилий для надкрановой части колонны

Вид усилия	Величины усилий в комбинациях
	Mmax	Mmin	Nmax
M, кН∙м	58,61	-57,38	30,28
N, кН	-447,36	-333,47	-460,02

Усилия от всех нагрузок без учета крановых и ветровых :

M^' = 30,28 кН∙м; N^' = -460,02 кН.

Усилия от продолжительно действующих (постоянных) нагрузок

M₁ = 18,32 кН∙м; N₁ = -333,468 кН.

Расчет в плоскости изгиба для M_max

Расчетная длина надкрановой части колонны в плоскости изгиба по табл.23 [5]: при учете крановых нагрузок l₀ = ψ∙H = 2∙H₁ = 2∙4,5 = 9 м; без учета крановых нагрузок l₀ = 2,5∙H₁ = 2,5∙4,5 = 11,25 м. Так как минимальная гибкость в плоскости изгиба l₀/h = 9/0,6 = 15 > 4, необходимо учитывать влияние прогиба колонны на ее несущую способность.

Устанавливаем значение коэффициента условий работы бетона γ_b2, для чего находим моменты внешних сил относительно центра тяжести растянутой (менее сжатой) арматуры с учетом и без учета крановых и ветровых нагрузок:

M_II-II = M₁ = M + N∙(0,5∙h - a) = 58,61 + 447,36∙(0,5∙0,6 - 0,04) = 174,92кН∙м;

M' _II-II = M^' + N^'∙(0,5∙h - a) = 30,28 + 460,08∙(0,5∙0,6 - 0,04) = 186,69 кН∙м.

Здесь знак момента от продольной силы определяется знаком момента M c учетом крановых и ветровых нагрузок.

Так как | M' _II-II | = 186,69 кН∙м > 0,82 | M_II-II | = 0,82∙174,92 = 143,44 кН∙м, то коэффициент условий работы бетона γ_b2 = 0,9; тогда расчетные сопротивления бетона R_b = 0,9∙17 = 15.3 МПа и R_bt = 0,9∙1,15 = 1.04 МПа.

Случайные эксцентриситеты:

e_a1 = l₀/600 = 11,25/600 = 0,019 м = 19 мм;

e_a2 = h/30 = 0,6/30 = 0,02 м = 20 мм; e_a3 = 10 мм.

Проектный эксцентриситет e₀ = |M|/N = 58,61/447,36 = 0,13 м = 130 мм > e_a1 = 19 мм, следовательно, случайный эксцентриситет не учитываем.

Находим условную критическую силу N_cr и коэффициент увеличения начального эксцентриситета η.

δ_e = e₀/h = 130/600 = 0,218 > δ_e,min = 0,5 - 0,01l₀/h - 0,01∙R_b = 0,5 - 0,01∙15 - 0,01∙15,3 = 0,197.

Если моменты M и M₁ имеют разные знаки, а эксцентриситет

e₀ = 130 мм > 0,1∙h = 0,1∙600 = 60 мм, то принимаем коэффициент φ_l = 1, если это условие не удовлетворяется, значение l принимают равным l = + 10(1 – )е0/h, где определяют по формуле

изгибающий момент в сечении 2-2 от постоянной нагрузки относительно центра тяжести растянутого стержня арматуры:

;

тогда, ;

= + 10(1 – )е0/h=1,6+10(1-1,6)130/600=0,29

Задаемся в первом приближении коэффициентом армирования

μ = 0,005.

Условная критическая сила

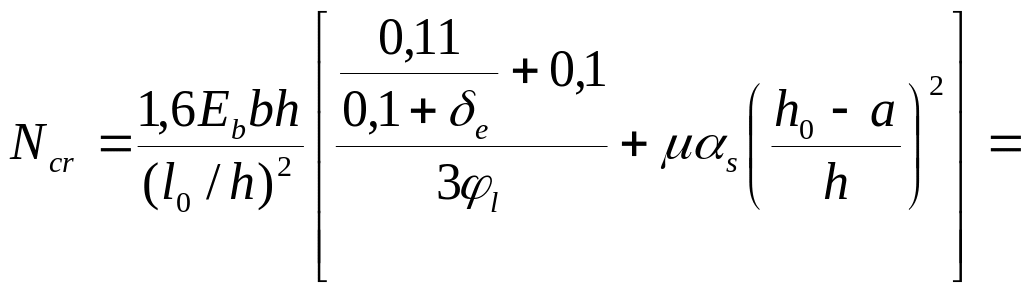
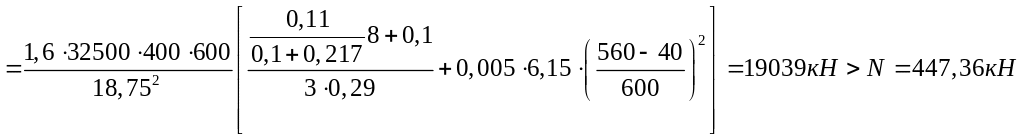- размеры сечения достаточны.

Коэффициент увеличения начального эксцентриситета

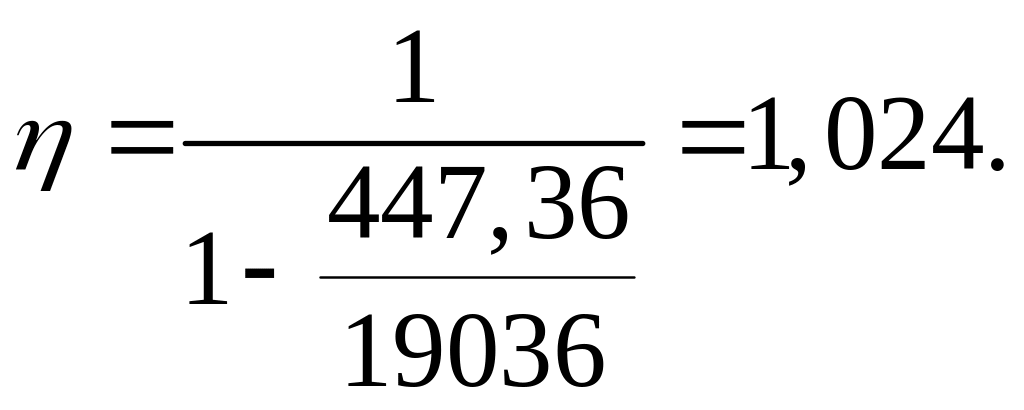
Расчетный эксцентриситет продольной силы

e = η∙e₀ + 0,5∙h - a = 1,024∙130 + 0,5∙600 - 40 = 394,17 мм.

Определим требуемую площадь сечения симметричной арматуры:

1.

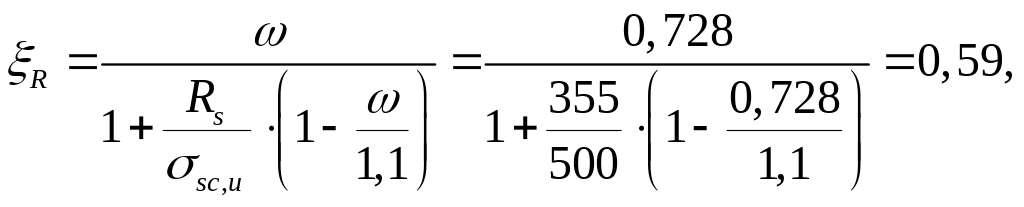
где ω = 0,85 - 0,008∙R_b = 0,85 - 0,008∙15,3 = 0,728;

σ_sc,u = 500 МПа при γ_в2 =0, 9.

2.

3.

4. δ = a/h₀ = 0,071.

При α_n = 0,131 < ξ_R = 0,59 требуемая площадь сечения симметричной арматуры составляет.

По конструктивным требованиям минимальная площадь сечения продольной арматуры при гибкости l₀/h ≤ 24 составляет

A_s,min = 0,002∙bh₀ = 0,002∙400∙560 = 448 мм².

Окончательно принимаем в надкрановой части колонны у граней, перпендикулярных плоскости изгиба по 2Ø18 А400 (A_s = A_s^' = 509 мм² > A_s,min = 448 мм²).

Коэффициент армирования сечения

- незначительно отличается от первоначально принятого μ = 0,005, поэтому корректировку расчета можно не производить.

Расчет из плоскости изгиба. За высоту сечения принимаем его размер из плоскости поперечной рамы, т.е. в этом случае h = b = 400 мм. Расчетная длина надкрановой части из плоскости составляет l₀ = ψ∙H = 1,5∙H₁ = 1,5∙4,5 = 6,75 м [5, табл.23]. Так как гибкость из плоскости l₀/b = 6,75/0,5 = 13,5 меньше гибкости в плоскости изгиба l₀/h = 18,75, расчет из плоскости изгиба можно не выполнять.

Расчет в плоскости изгиба для M_min

Расчетная длина надкрановой части колонны в плоскости изгиба по табл.23 [5]: при учете крановых нагрузок l₀ = ψ∙H = 2∙H₁ = 2∙4,5 = 9 м; без учета крановых нагрузок l₀ = 2,5∙H₁ = 2,5∙4,5 = 11,25 м. Так как минимальная гибкость в плоскости изгиба l₀/h = 9/0,6 = 15 > 4, необходимо учитывать влияние прогиба колонны на ее несущую способность.

Устанавливаем значение коэффициента условий работы бетона γ_b2, для чего находим моменты внешних сил относительно центра тяжести растянутой (менее сжатой) арматуры с учетом и без учета крановых и ветровых нагрузок:

M_II-II = M₁ = M + N∙(0,5∙h - a) = 29,32 кН∙м;

M' _II-II = M^' + N^'∙(0,5∙h - a) = 186,69 кН∙м.

Здесь знак момента от продольной силы определяется знаком момента M c учетом крановых и ветровых нагрузок.

Так как | M' _II-II | = 186,69 кН∙м > 0,82 | M_II-II | = 24,04 кН∙м, то коэффициент условий работы бетона γ_b2 = 0,9; тогда расчетные сопротивления бетона R_b = 0,9∙17 = 15.3 МПа и R_bt = 0,9∙1,15 = 1.04 МПа.

Случайные эксцентриситеты:

e_a1 = l₀/600 = 11,25/600 = 0,019 м = 19 мм;

e_a2 = h/30 = 0,6/30 = 0,02 м = 20 мм; e_a3 = 10 мм.

Проектный эксцентриситет e₀ = |M|/N =0 ,172 м = 172 мм > e_a1 = 19 мм, следовательно, случайный эксцентриситет не учитываем.

Находим условную критическую силу N_cr и коэффициент увеличения начального эксцентриситета η.

δ_e = e₀/h = 0,287 > δ_e,min = 0,5 - 0,01l₀/h - 0,01∙R_b = 0,5 - 0,01∙15 - 0,01∙15,3 = 0,197.

Если моменты M и M₁ имеют разные знаки, а эксцентриситет

e₀ = 172 мм > 0,1∙h = 0,1∙600 = 60 мм, то принимаем коэффициент φ_l = 1

Задаемся в первом приближении коэффициентом армирования

μ = 0,005.

Условная критическая сила

5369 кН>333,47 кН

- размеры сечения достаточны.

Коэффициент увеличения начального эксцентриситета

Расчетный эксцентриситет продольной силы

e = η∙e₀ + 0,5∙h - a = 443,47 мм.

Определим требуемую площадь сечения симметричной арматуры:

1.

где ω = 0,85 - 0,008∙R_b = 0,85 - 0,008∙15,3 = 0,728;

σ_sc,u = 500 МПа при γ_в2 =0, 9.

2.

3.

4. δ = a/h₀ = 0,071.

При α_n = 0,097 < ξ_R = 0,59 требуемая площадь сечения симметричной арматуры составляет.

По конструктивным требованиям минимальная площадь сечения продольной арматуры при гибкости l₀/h ≤ 24 составляет

A_s,min = 0,002∙bh₀ = 0,002∙400∙560 = 448 мм².

Окончательно принимаем в надкрановой части колонны у граней, перпендикулярных плоскости изгиба по 2Ø18 А400 (A_s = A_s^' = 509 мм² > A_s,min = 448 мм²).

Коэффициент армирования сечения

- незначительно отличается от первоначально принятого μ = 0,005, поэтому корректировку расчета можно не производить.

Расчет из плоскости изгиба. За высоту сечения принимаем его размер из плоскости поперечной рамы, т.е. в этом случае h = b = 400 мм. Расчетная длина надкрановой части из плоскости составляет l₀ = ψ∙H = 1,5∙H₁ = 1,5∙4,5 = 6,75 м. Так как гибкость из плоскости l₀/b = 6,75/0,5 = 13,5 меньше гибкости в плоскости изгиба l₀/h = 18,75, расчет из плоскости изгиба можно не выполнять.

Расчет в плоскости изгиба для N_max

Расчетная длина надкрановой части колонны в плоскости изгиба по табл.23 [5]: при учете крановых нагрузок l₀ = ψ∙H = 2∙H₁ = 2∙4,5 = 9 м; без учета крановых нагрузок l₀ = 2,5∙H₁ = 2,5∙4,5 = 11,25 м. Так как минимальная гибкость в плоскости изгиба l₀/h = 9/0,6 = 15 > 4, необходимо учитывать влияние прогиба колонны на ее несущую способность.

Устанавливаем значение коэффициента условий работы бетона γ_b2, для чего находим моменты внешних сил относительно центра тяжести растянутой (менее сжатой) арматуры с учетом и без учета крановых и ветровых нагрузок:

M_II-II = M₁ = M + N∙(0,5∙h - a) = 149,89 кН∙м;

M' _II-II = M^' + N^'∙(0,5∙h - a) = 186,69 кН∙м.

Здесь знак момента от продольной силы определяется знаком момента M c учетом крановых и ветровых нагрузок.

Так как | M' _II-II | = 186,69 кН∙м > 0,82 | M_II-II | = 122,91 кН∙м, то коэффициент условий работы бетона γ_b2 = 0,9; тогда расчетные сопротивления бетона R_b = 0,9∙17 = 15,3 МПа и R_bt = 0,9∙1,15 = 1.04 МПа.

Случайные эксцентриситеты:

e_a1 = l₀/600 = 11,25/600 = 0,019 м = 19 мм;

e_a2 = h/30 = 0,6/30 = 0,02 м = 20 мм; e_a3 = 10 мм.

Проектный эксцентриситет e₀ = |M|/N =0 ,066 м = 66 мм > e_a1 = 19 мм, следовательно, случайный эксцентриситет не учитываем.

Находим условную критическую силу N_cr и коэффициент увеличения начального эксцентриситета η.

δ_e = e₀/h = 0,11 < δ_e,min = 0,5 - 0,01l₀/h - 0,01∙R_b = 0,5 - 0,01∙15 - 0,01∙15,3 = 0,197. Принимаем δ_e =0,197

Если моменты M и M₁ имеют разные знаки, а эксцентриситет

e₀ = 66 мм > 0,1∙h = 0,1∙600 = 60 мм, то принимаем коэффициент φ_l = 1

если это условие не удовлетворяется, значение l принимают равным l = + 10(1 – )е0/h, где определяют по формуле

изгибающий момент в сечении 2-2 от постоянной нагрузки относительно центра тяжести растянутого стержня арматуры:

;

тогда, ;

= + 10(1 – )е0/h=1,7

Задаемся в первом приближении коэффициентом армирования

μ = 0,005.

Условная критическая сила

8750 кН>460,02 кН

- размеры сечения достаточны.

Коэффициент увеличения начального эксцентриситета

Расчетный эксцентриситет продольной силы

e = η∙e₀ + 0,5∙h - a = 329,48 мм.

Определим требуемую площадь сечения симметричной арматуры:

1.

где ω = 0,85 - 0,008∙R_b = 0,85 - 0,008∙15,3 = 0,728;

σ_sc,u = 500 МПа при γ_в2 =0, 9.

2.

3.

4. δ = a/h₀ = 0,071.

При α_n = 0,134 < ξ_R = 0,59 требуемая площадь сечения симметричной арматуры составляет.

По конструктивным требованиям минимальная площадь сечения продольной арматуры при гибкости l₀/h ≤ 24 составляет

A_s,min = 0,002∙bh₀ = 0,002∙400∙560 = 448 мм².

Окончательно принимаем в надкрановой части колонны у граней, перпендикулярных плоскости изгиба по 2Ø18 А400 (A_s = A_s^' = 509 мм² > A_s,min = 448 мм²).

Коэффициент армирования сечения

- незначительно отличается от первоначально принятого μ = 0,005, поэтому корректировку расчета можно не производить.

Расчет из плоскости изгиба. За высоту сечения принимаем его размер из плоскости поперечной рамы, т.е. в этом случае h = b = 400 мм. Расчетная длина надкрановой части из плоскости составляет l₀ = ψ∙H = 1,5∙H₁ = 1,5∙4,5 = 6,75 м. Так как гибкость из плоскости l₀/b = 6,75/0,5 = 13,5 меньше гибкости в плоскости изгиба l₀/h = 18,75, расчет из плоскости изгиба можно не выполнять.

5.2 Расчет подкрановой части колонны

Размеры сечения подкрановой части b = 400 мм; h = h₂ = 800 мм; a = a^' = 40 мм; h₀ = 800 - 40 = 760 мм.

Комбинации усилий для подкрановой части колонны

Вид усилия	Величины усилий в комбинациях
	Mmax	Mmin	Nmax
M, кН∙м	280,23	-180,28	50,79
N, кН	-945,86	-572,4	-987,36
Q, кН		22,58	9,95

Усилия от всех нагрузок без учета крановых и ветровых:

M^' = -16,41 кН∙м; N^' = -698,95 кН; усилия от продолжительных нагрузок: M_l = -8,77 кН∙м; N_l = -572,4 кН.

При наличии знакопеременных моментов армирование подкрановой части колонны также принимаем симметричным.

Расчет в плоскости изгиба для M_max

Расчетная длина надкрановой части колонны в плоскости изгиба по табл.23 [5]: при учете крановых нагрузок l₀ = ψ∙H = 1,5∙H₁ = 1,5∙7,95 = 11,93 м; без учета крановых нагрузок l₀ = 1,5∙H₁ = 1,5∙7,95 = 11,93 м. Так как минимальная гибкость в плоскости изгиба l₀/h = 11,93/0,6 = 15 > 4, необходимо учитывать влияние прогиба колонны на ее несущую способность.

Устанавливаем значение коэффициента условий работы бетона γ_b2, для чего находим моменты внешних сил относительно центра тяжести растянутой (менее сжатой) арматуры с учетом и без учета крановых и ветровых нагрузок:

M_II-II = M₁ = M + N∙(0,5∙h - a) = 620,74 кН∙м;

M' _II-II = M^' + N^'∙(0,5∙h - a) = 291,13 кН∙м.

Здесь знак момента от продольной силы определяется знаком момента M c учетом крановых и ветровых нагрузок.

Так как | M' _II-II | = 291,74 кН∙м < 0,82 | M_II-II | = 509,01 кН∙м, то коэффициент условий работы бетона γ_b2 = 1,1; тогда расчетные сопротивления бетона R_b = 1,1∙17 = 18,7 МПа и R_bt = 1,1∙1,15 = 1,265 МПа.

Случайные эксцентриситеты:

e_a1 = l₀/600 = 0,02 м = 20 мм;

e_a2 = h/30 = 0,027 м = 20 мм; e_a3 = 10 мм.

Проектный эксцентриситет e₀ = |M|/N =0 ,296 м = 296 мм > e_a1 = 20 мм, следовательно, случайный эксцентриситет не учитываем.

Находим условную критическую силу N_cr и коэффициент увеличения начального эксцентриситета η.

δ_e = e₀/h = 0,37 > δ_e,min = 0,5 - 0,01l₀/h - 0,01∙R_b = -1,18.

Если моменты M и M₁ имеют разные знаки, а эксцентриситет

e₀ = 296 мм > 0,1∙h = 0,1∙800 = 80 мм, то принимаем коэффициент φ_l = 1

Задаемся в первом приближении коэффициентом армирования

μ = 0,005.

Условная критическая сила

10201 кН>945,867 кН

- размеры сечения достаточны.

Коэффициент увеличения начального эксцентриситета

Расчетный эксцентриситет продольной силы

e = η∙e₀ + 0,5∙h - a = 686,55 мм.

Определим требуемую площадь сечения симметричной арматуры:

1.

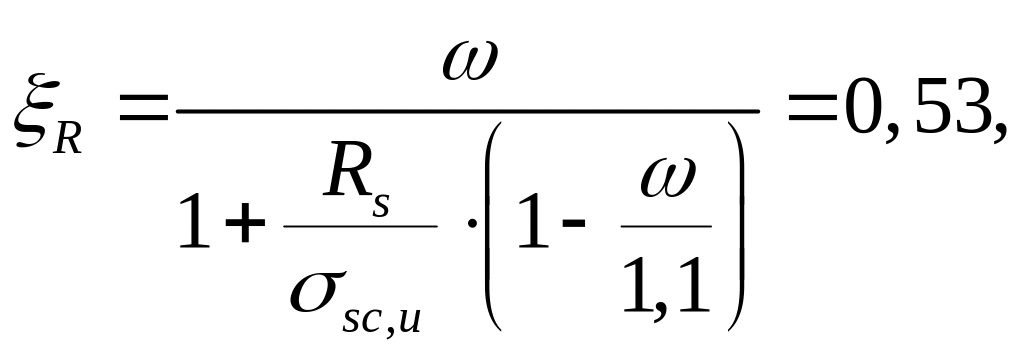
где ω = 0,85 - 0,008∙R_b = 0,85 - 0,008∙18,7 = 0,7;

σ_sc,u = 400 МПа при γ_в2 =1, 1.

2.

3.

4. δ = a/h₀ = 0,053.

При α_n = 0,166 < ξ_R = 0,53 требуемая площадь сечения симметричной арматуры составляет.

По конструктивным требованиям минимальная площадь сечения продольной арматуры при гибкости l₀/h ≤ 24 составляет

A_s,min = 0,002∙bh₀ = 0,002∙400∙760 = 608 мм².

Принимаем по 3Ø18 A400 (A_s = A_s^' = 763 мм² у коротких граней подкрановой части колонны.

Коэффициент армирования сечения

- незначительно отличается от первоначально принятого μ = 0,005, поэтому корректировку расчета можно не производить.

Расчет из плоскости изгиба. За высоту сечения принимаем его размер из плоскости поперечной рамы, т.е. в этом случае h = b = 400 мм. Расчетная длина надкрановой части из плоскости составляет l₀ = 0,8∙H₂ = 0,8∙7,95 = 6,36 м. Так как гибкость из плоскости l₀/b = 6,36/0,5 = 12,72 меньше минимальной гибкости в плоскости изгиба l₀/h = 14,9, расчет из плоскости изгиба можно не выполнять.

Расчет в плоскости изгиба для M_min

Расчетная длина надкрановой части колонны в плоскости изгиба по табл.23 [5]: при учете крановых нагрузок l₀ = ψ∙H = 1,5∙H₁ = 1,5∙7,95 = 11,93 м; без учета крановых нагрузок l₀ = 1,5∙H₁ = 1,5∙7,95 = 11,93 м. Так как минимальная гибкость в плоскости изгиба l₀/h = 11,93/0,6 = 15 > 4, необходимо учитывать влияние прогиба колонны на ее несущую способность.

Устанавливаем значение коэффициента условий работы бетона γ_b2, для чего находим моменты внешних сил относительно центра тяжести растянутой (менее сжатой) арматуры с учетом и без учета крановых и ветровых нагрузок:

M_II-II = M₁ = M + N∙(0,5∙h - a) = 25.78 кН∙м;

M' _II-II = M^' + N^'∙(0,5∙h - a) = 291,13 кН∙м.

Здесь знак момента от продольной силы определяется знаком момента M c учетом крановых и ветровых нагрузок.

Так как | M' _II-II | = 291,74 кН∙м > 0,82 | M_II-II | = 21,14 кН∙м, то коэффициент условий работы бетона γ_b2 = 0,9; тогда расчетные сопротивления бетона R_b = 0.9∙17 = 15.3 МПа и R_bt = 0.9∙1.15 = 1.04 МПа.

Случайные эксцентриситеты:

e_a1 = l₀/600 = 0,02 м = 20 мм;

e_a2 = h/30 = 0,027 м = 20 мм; e_a3 = 10 мм.

Проектный эксцентриситет e₀ = |M|/N =0 ,315 м = 315 мм > e_a1 = 20 мм, следовательно, случайный эксцентриситет не учитываем.

Находим условную критическую силу N_cr и коэффициент увеличения начального эксцентриситета η.

δ_e = e₀/h = 0,39 > δ_e,min = 0,5 - 0,01l₀/h - 0,01∙R_b = -1,14.

Если моменты M и M₁ имеют разные знаки, а эксцентриситет

e₀ = 315 мм > 0,1∙h = 0,1∙800 = 80 мм, то принимаем коэффициент φ_l = 1

если это условие не удовлетворяется, значение l принимают равным l = + 10(1 – )е0/h, где определяют по формуле

изгибающий момент в сечении 2-2 от постоянной нагрузки относительно центра тяжести растянутого стержня арматуры:

;

тогда, ;

= + 10(1 – )е0/h=-21,47

Задаемся в первом приближении коэффициентом армирования

μ = 0,005.

Условная критическая сила

1491 кН>572,4 кН

- размеры сечения достаточны.

Коэффициент увеличения начального эксцентриситета

Расчетный эксцентриситет продольной силы

e = η∙e₀ + 0,5∙h - a = 871,17 мм.

Определим требуемую площадь сечения симметричной арматуры:

1.

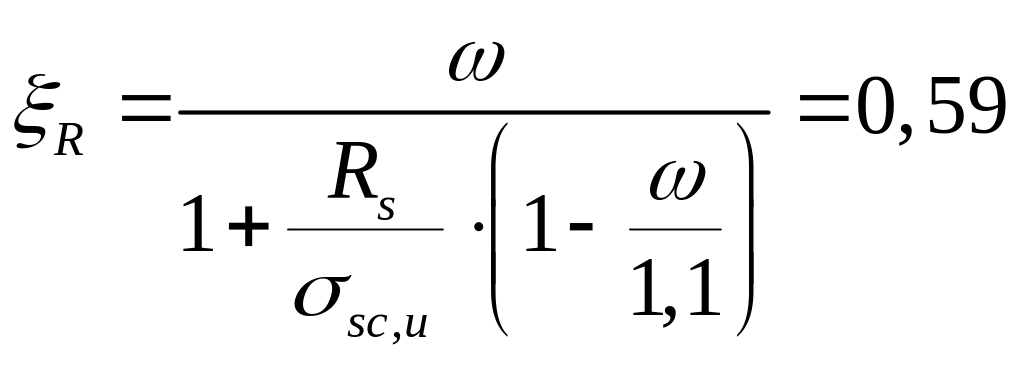
где ω = 0,85 - 0,008∙R_b = 0,85 - 0,008∙18,7 = 0,728;

σ_sc,u = 500 МПа при γ_в2 =0,9.

2.

3.

4. δ = a/h₀ = 0,053.

При α_n = 0,123 < ξ_R = 0,59 требуемая площадь сечения симметричной арматуры составляет.

По конструктивным требованиям минимальная площадь сечения продольной арматуры при гибкости l₀/h ≤ 24 составляет

A_s,min = 0,002∙bh₀ = 0,002∙400∙760 = 608 мм².

Принимаем по 3Ø18 A400 (A_s = A_s^' = 763 мм² у коротких граней подкрановой части колонны.

Коэффициент армирования сечения

- незначительно отличается от первоначально принятого μ = 0,005, поэтому корректировку расчета можно не производить.

Расчет из плоскости изгиба. За высоту сечения принимаем его размер из плоскости поперечной рамы, т.е. в этом случае h = b = 400 мм. Расчетная длина надкрановой части из плоскости составляет l₀ = 0,8∙H₂ = 0,8∙7,95 = 6,36 м. Так как гибкость из плоскости l₀/b = 6,36/0,5 = 12,72 меньше минимальной гибкости в плоскости изгиба l₀/h = 14,9, расчет из плоскости изгиба можно не выполнять.

Расчет в плоскости изгиба для N_max

Расчетная длина надкрановой части колонны в плоскости изгиба по табл.23 [5]: при учете крановых нагрузок l₀ = ψ∙H = 1,5∙H₁ = 1,5∙7,95 = 11,93 м; без учета крановых нагрузок l₀ = 1,5∙H₁ = 1,5∙7,95 = 11,93 м. Так как минимальная гибкость в плоскости изгиба l₀/h = 11,93/0,6 = 15 > 4, необходимо учитывать влияние прогиба колонны на ее несущую способность.

Устанавливаем значение коэффициента условий работы бетона γ_b2, для чего находим моменты внешних сил относительно центра тяжести растянутой (менее сжатой) арматуры с учетом и без учета крановых и ветровых нагрузок:

M_II-II = M₁ = M + N∙(0,5∙h - a) = 406,24 кН∙м;

M' _II-II = M^' + N^'∙(0,5∙h - a) = 291,13 кН∙м.

Здесь знак момента от продольной силы определяется знаком момента M c учетом крановых и ветровых нагрузок.

Так как | M' _II-II | = 291,74 кН∙м < 0,82 | M_II-II | = 333,17 кН∙м, то коэффициент условий работы бетона γ_b2 = 1,1; тогда расчетные сопротивления бетона R_b = 1,1∙17 = 18,7 МПа и R_bt = 1,1∙1,15 = 1,265 МПа.

Случайные эксцентриситеты:

e_a1 = l₀/600 = 0,02 м = 20 мм;

e_a2 = h/30 = 0,027 м = 27 мм; e_a3 = 10 мм.

Проектный эксцентриситет e₀ = |M|/N =0 ,051 м = 51 мм > e_a1 = 20 мм, следовательно, случайный эксцентриситет не учитываем.

Находим условную критическую силу N_cr и коэффициент увеличения начального эксцентриситета η.

δ_e = e₀/h = 0,06 > δ_e,min = 0,5 - 0,01l₀/h - 0,01∙R_b = -1,18.

Если моменты M и M₁ имеют разные знаки, а эксцентриситет

e₀ = 315 мм > 0,1∙h = 0,1∙800 = 80 мм, то принимаем коэффициент φ_l = 1

Задаемся в первом приближении коэффициентом армирования

μ = 0,005.

Условная критическая сила

21076 кН>987,36 кН

- размеры сечения достаточны.

Коэффициент увеличения начального эксцентриситета

Расчетный эксцентриситет продольной силы

e = η∙e₀ + 0,5∙h - a = 413,99 мм.

Определим требуемую площадь сечения симметричной арматуры:

1.

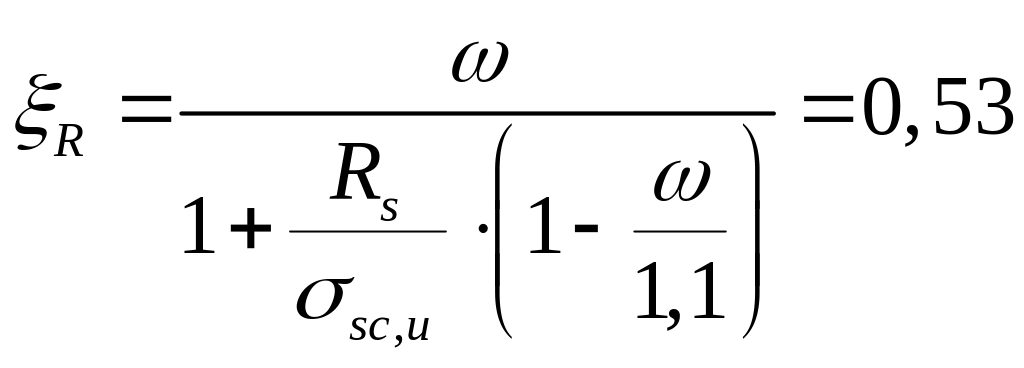
где ω = 0,85 - 0,008∙R_b = 0,85 - 0,008∙18,7 = 0,70;

σ_sc,u = 400 МПа при γ_в2 =0,9.

2.

3.

4. δ = a/h₀ = 0,053.

При α_n = 0,174 < ξ_R = 0,59 требуемая площадь сечения симметричной арматуры составляет.

По конструктивным требованиям минимальная площадь сечения продольной арматуры при гибкости l₀/h ≤ 24 составляет

A_s,min = 0,002∙bh₀ = 0,002∙400∙760 = 608 мм².

Принимаем по 3Ø18 A400 (A_s = A_s^' = 763 мм² у коротких граней подкрановой части колонны.

Коэффициент армирования сечения

- незначительно отличается от первоначально принятого μ = 0,005, поэтому корректировку расчета можно не производить.

Расчет из плоскости изгиба. За высоту сечения принимаем его размер из плоскости поперечной рамы, т.е. в этом случае h = b = 400 мм. Расчетная длина надкрановой части из плоскости составляет l₀ = 0,8∙H₂ = 0,8∙7,95 = 6,36 м. Так как гибкость из плоскости l₀/b = 6,36/0,5 = 12,72 меньше минимальной гибкости в плоскости изгиба l₀/h = 14,9, расчет из плоскости изгиба можно не выполнять.