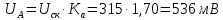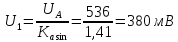№3
Определить
предел абсолютной и относительной
погрешности измерения напряжения, если
измерения проводились магнитоэлектрическим
прибором с классом точности
 и пределом измерения
и пределом измерения
 .
Результат измерения
.
Результат измерения
 В.
Вольтметр с нулём в начале шкалы.
В.
Вольтметр с нулём в начале шкалы.
Решение
1.
 В
– нормирующее значение;
В
– нормирующее значение;
Значение абсолютной погрешности будет равно:
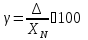 ; (3.1)
; (3.1)
 В; (3.2)
В; (3.2)
Где
 - приведённая погрешность (класс точность
прибора);
- приведённая погрешность (класс точность
прибора);
 -
абсолютная погрешность.
-
абсолютная погрешность.
2. Значение относительной погрешности будет равно:
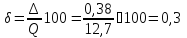 ; (3.3)
; (3.3)
Ответ:
 В,
В,
 .
.
№12
Обработать ряд наблюдений, полученный в процессе многократных прямых измерений физической величины (ФВ), и оценить случайную погрешность измерений, считая результаты исправленными и равноточными. Результат измерения представить по одной из форм МИ 1317-86 или ГОСТ 8.207-76. Вид ФВ – U, Размерность – мкВ, число наблюдений – N=15. Результаты наблюдения:
Таблица 1
|
I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Xi |
17,2714 |
19,2087 |
17,2570 |
17,3044 |
17,5808 |
17,2839 |
18,0627 |
17,2912 |
18,0420 |
Продолжение таблицы 1
|
I |
10 |
11 |
12 |
13 |
14 |
15 |
|
Xi |
17,3481 |
17,2767 |
17,8749 |
17,2979 |
17,9177 |
17,4381 |
Доверительная
вероятноcть
 .
.
Решение
1. Так как в условии задачи указано, что результаты измерения являются исправленными и равноточными, то производить исключение систематических погрешностей нет необходимости.
2. Вычисляем среднее арифметическое результатов наблюдений:

3. Определяем случайные отклонения Vi результатов отдельных наблюдений по формуле
Vi
= Xi
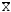 (12.2)
(12.2)
Результаты промежуточных расчетов заносим в таблицу 2.
Таблица 2
|
L |
1 |
2 |
3 |
4 |
5 |
|
Vi |
-0,3590 |
1,5783 |
-0,3734 |
-0,3260 |
-0,0496 |
|
V2i |
0,1289 |
2,4911 |
0,1394 |
0,1063 |
0,0025 |
Продолжение таблицы 2
|
L |
6 |
7 |
8 |
9 |
10 |
|
Vi |
-0,3465 |
0,4323 |
-0,3392 |
0,4116 |
-0,2823 |
|
V2i |
0,1200 |
0,1869 |
0,1150 |
0,1694 |
0,0797 |
Продолжение таблицы 2
|
L |
11 |
12 |
13 |
14 |
15 |
|
Vi |
-0,3537 |
0,2445 |
-0,3325 |
0,2873 |
-0,1923 |
|
V2i |
0,1251 |
0,0598 |
0,1105 |
0,0826 |
0,0370 |
4.
Вычисляем оценку среднего квадратического
отклонения результатов наблюдений
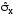 :
:
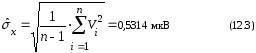
5.
С помощью критерия грубых погрешностей
(критерий «трёх сигм») проверяем наличие
грубых погрешностей. В соответствии с
этим критерием, если
 ,
то такое наблюдение содержит грубую
погрешность. В случае обнаружения грубой
погрешности в i-м наблюдении необходимо
это наблюдение исключить из результатов
наблюдений и повторить вычисления для
меньшего числа n.
,
то такое наблюдение содержит грубую
погрешность. В случае обнаружения грубой
погрешности в i-м наблюдении необходимо
это наблюдение исключить из результатов
наблюдений и повторить вычисления для
меньшего числа n.
 1,5943
мкВ.
1,5943
мкВ.
Грубые погрешности присутствуют. Это значение 19,2087. Проведём расчёт без него.
6. Вычисляем среднее арифметическое результатов наблюдений:
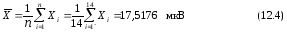
7. Определяем случайные отклонения VI результатов отдельных наблюдений по формуле
Vi
= Xi
 (12.5)
(12.5)
Результаты промежуточных расчетов заносим в таблицу 2.
Таблица 2
|
L |
1 |
2 |
3 |
4 |
5 |
|
Vi |
-0,2462 |
- |
-0,2606 |
-0,2132 |
0,0632 |
|
V2i |
0,0606 |
- |
0,0679 |
0,0455 |
0,0040 |
Продолжение таблицы 2
|
L |
6 |
7 |
8 |
9 |
10 |
|
Vi |
-0,2337 |
0,5451 |
-0,2264 |
0,5244 |
-0,1695 |
|
V2i |
0,0546 |
0,2971 |
0,0513 |
0,2750 |
0,0287 |
Продолжение таблицы 2
|
L |
11 |
12 |
13 |
14 |
15 |
|
Vi |
-0,2409 |
0,3573 |
-0,2197 |
0,4001 |
-0,0795 |
|
V2i |
0,0580 |
0,1276 |
0,0483 |
0,1601 |
0,0063 |
8.
Вычисляем оценку среднего квадратического
отклонения результатов наблюдений
 :
:

9. С помощью критерия грубых погрешностей (критерий «трёх сигм») проверяем наличие грубых погрешностей. Грубые погрешности отсутствуют.
10. Определяем
оценку среднего квадратического
отклонения результата измерения
 из выражения:
из выражения:

11. Выдвигаем гипотезу о принадлежности результатов наблюдений нормальному распределению и проверяем эту гипотезу.
В решаемой задаче n = 14. Поэтому принадлежность результатов наблюдений к нормальному распределению проверяем по составному критерию.
Критерий 1. Вычисляем смещённую оценку среднего квадратического отклонения по формуле:
 (12.8)
(12.8)
Вычисляем параметр
 (12.9)
(12.9)
Результаты наблюдений можно считать распределенными нормально, если
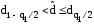 ,
где
,
где
 и
и
 - квантили распределения, причем
- квантили распределения, причем
q1
- заранее выбранный уровень значимости
критерия. Выбираем уровень значимости
q равным 5 %. Находим
 =
0,8884,
=
0,8884,
 =
0,7236. Сравнивая полученное значение
=
0,7236. Сравнивая полученное значение
 с этими величинами, делаем вывод о том,
что по критерию 1 результаты наблюдений
распределены по нормальному закону.
с этими величинами, делаем вывод о том,
что по критерию 1 результаты наблюдений
распределены по нормальному закону.
Критерий 2. Этот критерий используется дополнительно для проверки «концов» распределений.
Гипотеза
о нормальности по критерию 2 не отвергается,
если не более m разностей Vi
превзошли значение
 ,
где верная квантиль распределения
нормированной функции Лапласа отвечает
вероятности P/2.
,
где верная квантиль распределения
нормированной функции Лапласа отвечает
вероятности P/2.
Для
решаемой задачи выбираем уровень
значимости q2
= 5% и для n = 14 находим P = 0,98 и m = 1. Тогда,
обращаясь к таблице значений нормированной
функции Лапласа ф(z),
находим ZP/2
= 2,33. Отсюда
 = 0,7326 мкВ.
= 0,7326 мкВ.
Согласно критерию 2 не более одной (m = 1) разности Vi могут превзойти значение 0,7326 мкВ.
По данным, приведенным в таблице 2, видим, что ни одно V не превышает критическое значение. Следовательно, критерий 2 выполняется.
Таким образом, с уровнем значимости q q1+ q2 = 0,1 гипотеза о нормальности полученных данных согласуется с данными наблюдений.
12. По заданной доверительной вероятности Pд и числу степеней свободы (n1) распределения Стьюдента определим коэффициент t.
Для нашей задачи (P = 0,95 и n-1 = 13) значение t = 2,16.
Рассчитываем доверительные границы случайной погрешности результата измерения
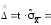 2,160,084
= 0,1815
мкВ (12.10)
2,160,084
= 0,1815
мкВ (12.10)
13. Записываем результат измерения.
При
симметричной доверительной погрешности
результаты измерений представляют в
виде
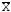
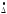 , Pд.
, Pд.
При
этом значащих цифр в
 должно быть не более двух , а числовое
значение результата измерения должно
оканчиваться цифрой того же разряда,
что и значение погрешности
должно быть не более двух , а числовое
значение результата измерения должно
оканчиваться цифрой того же разряда,
что и значение погрешности
 .
.
Результат измерения записываем в следующем виде:
U = (17,52 0,19) мкВ; Pд = 0,95 (12.11)
Ответ: U = (17,52 0,19) мкВ; Pд = 0,95.
№15
В
процессе обработки результатов прямых
измерений сопротивления определено:
среднее арифметическое значение этого
сопротивления
 кОм, границы неисключенных остатков
трёх составляющих систематической
погрешности
кОм, границы неисключенных остатков
трёх составляющих систематической
погрешности
 кОм,
кОм,
 кОм,
кОм,
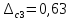 кОм. Требуется определить доверительные
границы суммарной погрешности результата
измерения и записать его в соответствии
МИ 1317-86 или ГОСТ 8.207-76. Значение доверительной
вероятности принять
кОм. Требуется определить доверительные
границы суммарной погрешности результата
измерения и записать его в соответствии
МИ 1317-86 или ГОСТ 8.207-76. Значение доверительной
вероятности принять
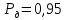 .
При расчётах полагать, что случайная
погрешность пренебрежительно мала, а
число наблюдений существенно больше
30.
.
При расчётах полагать, что случайная
погрешность пренебрежительно мала, а
число наблюдений существенно больше
30.
Решение
1. Т.к. случайная погрешность пренебрежительно мала, то доверительные границы случайной состовляющей:
 кОм (15.1)
кОм (15.1)
2. Определяем доверительные границы неисключенной систематической погрешности результата измерения
 (15.2)
(15.2)
где m - число суммируемых погрешностей;
 -
граница i-й неисключенной систематической
погрешности;
-
граница i-й неисключенной систематической
погрешности;
k - коэффициент, определяемый принятой доверительной вероятностью.
При доверительной вероятности Рд = 0,95 коэффициент k принимают равным 1,1.
Тогда:
 Ом
(15.3)
Ом
(15.3)
3. Определим границы суммарной погрешности результата измерения.
Границы погрешности результата измерения (без учета знака) вычисляют по формуле
 (15.4)
(15.4)
где К- коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;
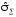 -
оценка суммарного среднего квадратического
отклонения результата измерения.
-
оценка суммарного среднего квадратического
отклонения результата измерения.
Значение
 вычисляют по формуле
вычисляют по формуле
 кОм
(15.5)
кОм
(15.5)
Коэффициент К вычисляют по эмпирической формуле
 (15.6)
(15.6)
Определяем доверительные границы суммарной погрешности результата измерения
 (15.7)
(15.7)
4. Записываем результат измерения. Так как погрешность симметрична относительно результата измерения, то
R = (53,8 2,8) кОм, Рд = 0,95 (15.8)
Ответ: R = (53,8 2,8) кОм, Рд = 0,95.
№18
Сопротивление
 определялось косвенным методом путём
многократных измерений (n=11) падения
напряжения на нём
определялось косвенным методом путём
многократных измерений (n=11) падения
напряжения на нём
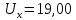 B
и падения напряжения
B
и падения напряжения
 B
на последовательно соединенным с ним
образцовом резисторе
B
на последовательно соединенным с ним
образцовом резисторе
 кОм с последующим расчётом
кОм с последующим расчётом
 .
Оценки средних квадратических отклонений
среднего арифметического
.
Оценки средних квадратических отклонений
среднего арифметического
 ,
,
 ,
оценка коэффициента корреляции между
погрешностями измерений
,
оценка коэффициента корреляции между
погрешностями измерений
 .
.
Определить случайную погрешность результата косвенного измерения с доверительной вероятностью Рд = 0,95 и записать результат по одной из установленных форм.
Решение
1. Находим значение результата косвенного измерения напряжения
 кОм
(18.1)
кОм
(18.1)
2. Определяем частные случайные погрешности косвенного измерения
 кОм;
(18.2)
кОм;
(18.2)
 кОм; (18.3)
кОм; (18.3)
3. Вычисляем оценку среднего квадратического отклонения результата косвенного измерения:

 кОм
(18.4)
кОм
(18.4)
4. Определяем значение коэффициента Стьюдента t для заданной до-верительной вероятности Рд и числа наблюдений n.
При n 30 предварительно должно быть определено так называемое «эффективное» число степеней свободы распределения Стьюдента,
Оно определяется из выражения
 ,
(18.5)
,
(18.5)
где ni - число наблюдений при прямых измерениях xi .
 - относительная оценка среднеквадратического
отклонения
- относительная оценка среднеквадратического
отклонения
Для
решаемой задачи

в) При получении дробного значения nэфф для нахождения коэффициента Стьюдента применяем линейную интерполяцию:
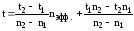 ,
(18.6)
,
(18.6)
где t1, t2 и n1, n2 - соответствующие табличные значения коэффициента Стьюдента и числа наблюдений (для заданной Рд), между которыми находится значение nэфф.
Для решаемой задачи при nэфф =10,2 и Рд = 0,95 находим n1 = 10,
t1 = 2,2281, n2 = 11, t2 = 2,201 , а затем вычисляем значение t = 2,223.
5. Вычисляем доверительные границы случайной погрешности результата косвенного измерения:
 кОм (18.7)
кОм (18.7)
6. Записываем результат измерения:
 кОм Рд=0,95.
(18.8)
кОм Рд=0,95.
(18.8)
7. Проанализируем полученные результаты с использованием критерия ничтожных погрешностей.
В соответствии с этим критерием, если частная погрешность меньше 1/3 суммарной погрешности, то она является «ничтожной» и может быть исключена из рассмотрения.
Для
решаемой задачи

 ;
;

Следовательно
частные погрешности
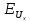 ,
,
 не считаются «ничтожными», и ими нельзя
пренебречь.
не считаются «ничтожными», и ими нельзя
пренебречь.
Ответ:
 кОм Рд=0,95.
кОм Рд=0,95.
№26
Рассчитать
сопротивление добавочного вольтметра
с ценой деления
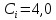 мВ/дел. и шкалой с
мВ/дел. и шкалой с
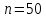 делениями, полученное при расширении
его предела измерения по напряжению до
значения
делениями, полученное при расширении
его предела измерения по напряжению до
значения
 В. Определить методическую погрешность
измерения тока при включении вольтметра
в цепь. Сопротивление нагрузки
В. Определить методическую погрешность
измерения тока при включении вольтметра
в цепь. Сопротивление нагрузки
 кОм, сопротивление источника ЭДС
кОм, сопротивление источника ЭДС
 кОм, внутреннее сопротивление вольтметра
кОм, внутреннее сопротивление вольтметра
 кОм.
кОм.
Решение
1. Напишем выражение для нахождения коэффициента расширения пределов измерения
 . (26.1)
. (26.1)
 предел
измерения вольтметра.
предел
измерения вольтметра.
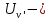 предел
измерения вольтметра после расширения.
предел
измерения вольтметра после расширения.
Рассчитаем
напряжение
 :
:
 мВ (26.2)
мВ (26.2)
Тогда

2. Сопротивление добавочного резистора будет равно:
 кОм (26.3)
кОм (26.3)
3. Методическая погрешность при включении амперметра в цепь будет равна:
 (26.4)
(26.4)
Ответ:
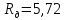 Ом;
Ом;  .
.
№31
Необходимо
определить пиковое Um,
среднее квадратическое Uск
и средневыпрямленное UСВ
значения напряжения, поданного на вход
электронного вольтметра с классом
точности
 ,
с пиковым детектором, закрытым входом,
со шкалой, проградуированной в
среднеквадратических значениях
синусоидального напряжения после
мостового выпрямителя. Показание
вольтметра U = 550 мВ. Сигнал
характеризуется коэффициентами
амплитуды Ка
=
1,41 и формы Кф
=
1,11, и подан в положительной полярности.
Оценить также пределы основных
инструментальных абсолютной и
относительной погрешностей измерения
U, выбрав необходимый предел измерения
из ряда предпочтительных чисел ... 3; 10;
30; 100 ... В.
,
с пиковым детектором, закрытым входом,
со шкалой, проградуированной в
среднеквадратических значениях
синусоидального напряжения после
мостового выпрямителя. Показание
вольтметра U = 550 мВ. Сигнал
характеризуется коэффициентами
амплитуды Ка
=
1,41 и формы Кф
=
1,11, и подан в положительной полярности.
Оценить также пределы основных
инструментальных абсолютной и
относительной погрешностей измерения
U, выбрав необходимый предел измерения
из ряда предпочтительных чисел ... 3; 10;
30; 100 ... В.
Решение
1. Так как вольтметр имеет закрытый вход, то измеряется только значение переменной составляющей сигнала Um, равное Um= Ка U = 1,41U, (детектор пиковый, а шкала вольтметра проградуирована в среднеквадратических значениях синусоидального напряжения).
2. Амплитудное значение напряжения определяется как сумма переменной и постоянной составляющих (средневыпрямленного значения):
 (31.1)
(31.1)
Тогда:
 (31.2)
(31.2)
3. Средневыпрямленное значение будет равно:
 мВ (31.3)
мВ (31.3)
4. Среднеквадратическое значение напряжения будет равно:
 мВ (31.4)
мВ (31.4)
Выберем
стандартный предел измерения, равный
1000 мВ. При увеличении предела измерения
при неизменном классе точности
увеличивается значение относительной
погрешности. Тогда нормированное
значение
 и приведённая погрешность
и приведённая погрешность
 % (класс точности).
% (класс точности).
 .
Вычислим
значение абсолютной погрешности:
.
Вычислим
значение абсолютной погрешности:
 (31.5)
(31.5)
6. Вычислим значение относительной погрешности:
 (31.6)
(31.6)

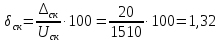

Ответ:
 мВ,
мВ,
 мВ,
мВ,
 мВ,
мВ,
 ,
,
 ,
,
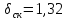 ,
,
 .
.
№35
Необходимо
по показанию вольтметра с детектором
средневыпрямленного значения
 определить показания вольтметров с
детекторами среднего квадратического
и пикового значений. Вольтметры имеют
открытые входы, шкалы их отградуированы
в средних квадратических значениях
синусоидального напряжения. Измеряемое
напряжение имеет коэффициент амплитуды
определить показания вольтметров с
детекторами среднего квадратического
и пикового значений. Вольтметры имеют
открытые входы, шкалы их отградуированы
в средних квадратических значениях
синусоидального напряжения. Измеряемое
напряжение имеет коэффициент амплитуды
 и формы
и формы
 .
.
Решение
1. Т.к. третий вольтметр имеет детектор средневыпрямленного значения, а его шкала отградуирована в средних квадратических значениях синусоидального напряжения, то средневыпрямленное значение напряжения будет равно:
|
|
(35.1) |
2. Среднее квадратическое значение сигнала будет равно:
|
|
(35.2) |
3. Т.к. второй вольтметр имеет детектор среднего квадратического значения, а его шкала отградуирована в средних квадратических значениях синусоидального напряжения, то его показание будет равно:
|
|
(35.3) |
4. Пиковое значение сигнала будет равно:
|
|
(35.4) |
5. Т.к. первый вольтметр имеет детектор пикового значения, а его шкала отградуирована в средних квадратических значениях синусоидального напряжения, то его показание будет равно:
|
|
(35.5) |
Ответ:
 ,
,
 .
.
№42
Цифровой
интегрирующий фазометр имеет постоянное
время измерения
 ,
разрешающую способность
,
разрешающую способность
 и частоту опорного генератора
и частоту опорного генератора
 .
.
Определить
 и перечислить составляющие инструментальной
погрешности измерения, изобразить
функциональную схему и временные
диаграммы, пояснить принцип действия.
и перечислить составляющие инструментальной
погрешности измерения, изобразить
функциональную схему и временные
диаграммы, пояснить принцип действия.
Решение
1.
Упрощенная структурная схема
однополупериодного интегрирующего
цифрового фазометра (ИЦФ), реализующая
алгоритм
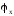 →
→ →
код представлена на рисунке 2.
→
код представлена на рисунке 2.

Рисунок 2 – Структурная схема однополупериодного ИЦФ
Сущность
метода заключается в преобразовании
фазового сдвига
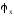 между двумя гармоническими сигналами
между двумя гармоническими сигналами
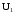 и
и
 ,
который необходимо измерить в
пропорциональный ему интервал времени
,
который необходимо измерить в
пропорциональный ему интервал времени
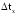 .
Затем измеряется отношение
.
Затем измеряется отношение
 к периоду сигналов
к периоду сигналов
 .
Математически это выглядит так:
.
Математически это выглядит так:
 и
и
 ,
т.е
,
т.е
 (42.1)
(42.1)
Суть
преобразования наглядно поясняется
следующими эпюрами (рисунок 3). Если
гармонические сигналы
 и
и
 (рисунок 3, а) с помощью формирующих
устройств преобразовать в последовательности
коротких импульсов
(рисунок 3, а) с помощью формирующих
устройств преобразовать в последовательности
коротких импульсов
 и
и
 ,
соответствующие моментам перехода этих
сигналов через ноль (рисунок 3, б; в
соответственно), то полученный интервал
времени
,
соответствующие моментам перехода этих
сигналов через ноль (рисунок 3, б; в
соответственно), то полученный интервал
времени
 между ближайшими импульсами одной
полярности будет пропорционален
между ближайшими импульсами одной
полярности будет пропорционален
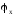 (рисунок 3,г).
(рисунок 3,г).
Далее,
на выходе селектора 1 образуются пачки
счетных импульсов (рисунок 3, д). Число
импульсов в пачке равно
 и определяется выражением:
и определяется выражением:
 (42.2)
(42.2)
Эти
пачки поступают на вход селектора 2,
который открыт на время действия
стробирующего импульса
 (рисунок 3, е). Этот импульс формируется
в УУ из импульсов ГСИ, путем понижения
их частоты следования в
(рисунок 3, е). Этот импульс формируется
в УУ из импульсов ГСИ, путем понижения
их частоты следования в
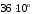 раз с помощью делителя частоты. Таким
образом
раз с помощью делителя частоты. Таким
образом
 =
=
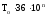 и обеспечивается выполнение необходимой
кратности между
и обеспечивается выполнение необходимой
кратности между
 и
и
 .
Число пачек счетных импульсов на выходе
селектора 2 (рисунок 3, ж) равно
.
Число пачек счетных импульсов на выходе
селектора 2 (рисунок 3, ж) равно
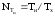 (42.3)
(42.3)
В
результате счетчик фиксирует число
импульсов N равное
 .
.
С учетом (42.2)
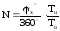 и
и
 (42.4)
(42.4)
Погрешность измерения складывается из случайной погрешности дискретности, т. е. возможности потери одного счетного импульса в группе, и возможности потери части группы в интервале усреднения.
 Рисунок
3 – Временные диаграммы, поясняющие
метод преобразования
Рисунок
3 – Временные диаграммы, поясняющие
метод преобразования
 →
→
 и работу фазометров
и работу фазометров
2.
С помощью формулы (42.3) рассчитаем время
измерения
 :
:
|
|
(42.5) |
Ответ:
 .
.
№51
Выбрать
оптимальный коэффициент развёртки
 из возможных (100 мкс/дел, 50 мкс/дел, 10
мкс/дел) для измерения длительности
импульса
из возможных (100 мкс/дел, 50 мкс/дел, 10
мкс/дел) для измерения длительности
импульса
 .
Размеры экрана ЭЛО – Y
x
X
= (8 x
10) дел.
.
Размеры экрана ЭЛО – Y
x
X
= (8 x
10) дел.
Решение
1.
Из возможных вариантов выберем коэффициент
развёртки
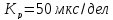 .
Тогда на экране будет наблюдаться три
полных импульса:
.
Тогда на экране будет наблюдаться три
полных импульса:
|
|
(51.3) |
Где 10 дел – количество делений по горизонтальной оси экрана;
50
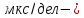 выбранный
коэффициент развёртки;
выбранный
коэффициент развёртки;
400
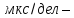 длительность
импульса.
длительность
импульса.
2.
При выборе коэффициента развёртки 10
мкс/дел наблюдаемый импульс не будет
полностью наблюдаться на экране, т.к.
150

Ответ:

№64
Охарактеризовать методы стандартизации – оганичение и типизацию. Привести примеры их применения при производстве систем телекоммуникаций. В чем выражается технико-экономический эффект от их применения?
Решение
Cтандартизация - деятельность по установлению технических требований в целях их всеобщего и многократного применения в отношении постоянно повторяющихся задач, направленная на достижение оптимальной степени упорядочения в области разработки, производства, эксплуатации (использования), хранения, перевозки, реализации и утилизации продукции или оказания услуг.
Основными методами стандартизации являются: ограничение (симплификация), типизация, унификация и агрегатирование. Рассмотрим Ограничение и типизацию.
Ограничение (симплификация) - метод стандартизации, заключающийся в отборе и рациональном ограничении номенклатуры объектов, разрешенных для применения в данной отрасли, на данном предприятии или в каком-либо объекте до числа, достаточного для удовлетворения существующих в данное время потребностей. При этом оставляются только те объекты, которые считают необходимыми, в них не вносят в дальнейшем какие-либо усовершенствования. Исторически этот метод сложился одним из первых и по сравнению с другими методами является простейшим.
Ограничение может проводиться практически на всех уровнях. В частности, национальные и международные стандарты могут быть ограничены стандартами предприятий. Кроме того, на правах стандартов каждое предприятие может разрабатывать ограничительные перечни, устанавливающие разрешенные к применению типы, виды и номенклатуру комплектующих изделий, узлов и материалов при разработке , изготовлении или модернизации каких-либо изделий, также ограничение на использование тех или иных НТД. Наконец, могут вводиться ограничения на виды используемых технологических процессов, элементы различных конструкций, номиналы электрических, физических и других параметров изделий и т.д. В результате уменьшается номенклатура и количество различных изделий, циркулирующих на предприятиях, снижается стоимость изготовления и эксплуатации продукции, повышается производительность труда и эффективность производства.
Типизация - метод стандартизации, заключающийся в рациональном сокращении видов объектов путем установления некоторых типовых видов, принимаемых за основу (базу) при создании других объектов, аналогичных или близких по функциональному назначению. Поэтому этот метод называют еще методом "базовых конструкций".
При типизации не только анализируются уже существующие типы и типоразмеры изделий, но и разрабатываются новые, перспективные, учитывающие новейшие достижения науки, техники и развитие промышленности. Типизация как метод стандартизации обеспечивает сохраняемость отдельных объектов из возможной совокупности, хотя каждый конкретный объект может претерпевать некоторые изменения или доработки для выполнения дополнительных функций.
Типизация получила широкое распространение в промышленности для стандартизации типовых изделий общего назначения и типовых технологических процессов (ТПП) изготовления изделий, а также методов их испытаний. Так, например, в радиопромышленности в настоящее время действует около 1000 ТПП. Характерно также применение этого метода при создании руководящих документов, устанавливающих порядок проведения каких-либо работ, расчетов и т.п. Применение типизации дает большой технико-экономический эффект, который реализуется в следующих направлениях:
- при проектировании новых изделий используются проверенные методы, базовые конструкции и модели, исключаются лишние поиски и возможные ошибки;
- обеспечивается большая преемственность в производстве при смене различных типов устройств, созданных на одной базе, а подготовка производства значительно ускоряется с одновременным снижением расходов на ее проведение;
- облегчаются условия эксплуатации и ремонта изделий, имеющих много общих конструктивных элементов.