Примеры.

1. Нулевой оператор: 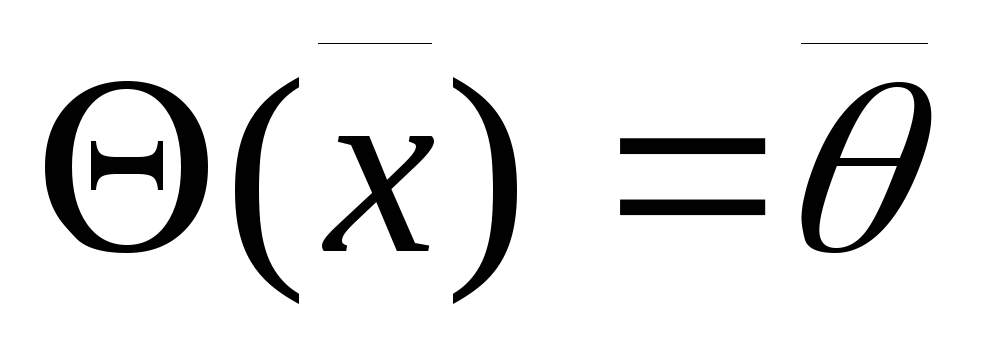, матрица нулевого оператора — нулевая матрица соответствующего порядка, т.е. т.е. — единственное собственное значение нулевого оператора, а соответствующие собственные векторы — все ненулевые векторы пространства X.

2. Тождественный (единичный) оператор I: матрица тождественного оператора — единичная матрица соответствующего порядка, т.е. т.е. — единственное собственное значение тождественного оператора, а соответствующие собственные векторы — все ненулевые векторы пространства X.

3. Оператор P₂ — оператор проектирования пространства R³ на подпространство R² параллельно вектору : , тогда матрица тождественного оператора — единичная матрица соответствующего порядка, т.е. т.е. и — собственные значения оператора.

Найдем соответствующие собственные векторы.

Пусть , тогда соответствующие собственные векторы — ненулевые решения системы т.е.

т.е. вектор

— собственный вектор оператора, отвечающий собственному значению и, следовательно, все векторы вида — собственные векторы оператора, отвечающие собственному значению .

Теперь положим , тогда соответствующие собственные векторы — ненулевые решения системы т.е.

т.е. векторы

— линейно независимые векторы, которые являются собственными векторами оператора, отвечающими собственному значению и, следовательно, все векторы вида — собственные векторы оператора, отвечающие собственному значению .

4. . Оператор U_ поворота пространства R² на угол φ относительно начала координат против часовой стрелки:.

Матрица оператора , тогда

Характеристическое уравнение имеет единственный корень при и при ,. Если , , и т.е. соответствующие собственные векторы — все ненулевые векторы пространства R².

При — оператор поворота не имеет собственных векторов.

И, наконец, при и , , оператор поворота совпадает с тождественным оператором, собственные значения и собственные векторы которого вычислены выше.

Свойства собственных векторов

Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения:

1. характеристический многочлен оператора, действующего в X_n является многочленом n -й степени относительно (б/д);

2. линейный оператор, действующий в X_n имеет не более n различных собственных значений (б/д);

3. корни характеристического многочлена не зависят от базиса (на лекции доказано) (б/д);

4. собственные векторы, отвечающие различным собственным значениям, линейно независимы (на лекции доказано).

31