1. Зависимость скорости реакции от температуры

   1. Правило Вант-Гоффа

С повышением температуры скорость реакции увеличивается. Зависимость скорости реакции от температуры приближенно описывается эмпирическим правилом Вант-Гоффа: при повышении температуры на каждые 10° скорость реакции увеличивается в 2-4 раза.

Математическое выражение правила Вант-Гоффа:

(16),

а при условии, что концентрации всех реагирующих веществ равны 1 моль/л:

(17),

где , и , - соответственно скорости и константы скоростей реакции при температурах и .

Температура может быть выражена как в °С, так и в К, так как изменение температуры не зависит от единиц измерения ( ).

- температурный коэффициент скорости реакции, который показывает, во сколько раз возрастает скорость реакции при повышении температуры на 10 градусов:

(18)

Поскольку при концентрациях реагирующих веществ 1 моль/л скорость химической реакции численно равна константе скорости , то

(19)

Учитывая тот факт, что скорость реакции обратно пропорциональна времени ее протекания из уравнения (18), при получаем

(20)

Используя уравнения (16 – 20), можно рассчитать:

• константу скорости (или скорость) реакции при заданной температуре, если известны значения этих величин при двух других температурах;

• на сколько градусов надо повысить (или понизить) температуру реакции, чтобы скорость ее увеличилась (или уменьшилась) в N раз;

• при какой температуре следует проводить реакцию, чтобы она закончилась за определенное время, если известны температурный коэффициент реакции и скорость ее при любой температуре;

• температурный коэффициент реакции и т. д.

Пример 7. Рассчитайте константу скорости химической реакции при °С, если константа скорости этой реакции при температурах 400 °С и 500 °С равна соответственно 0,03 и 50,3.

Решение

а). Для определения запишем уравнение Вант-Гоффа (17), используя или :

или

Учитывая:

, , получаем:

или (21)

б). Температурный коэффициент рассчитываем из отношения , полученного из уравнения (17):

.

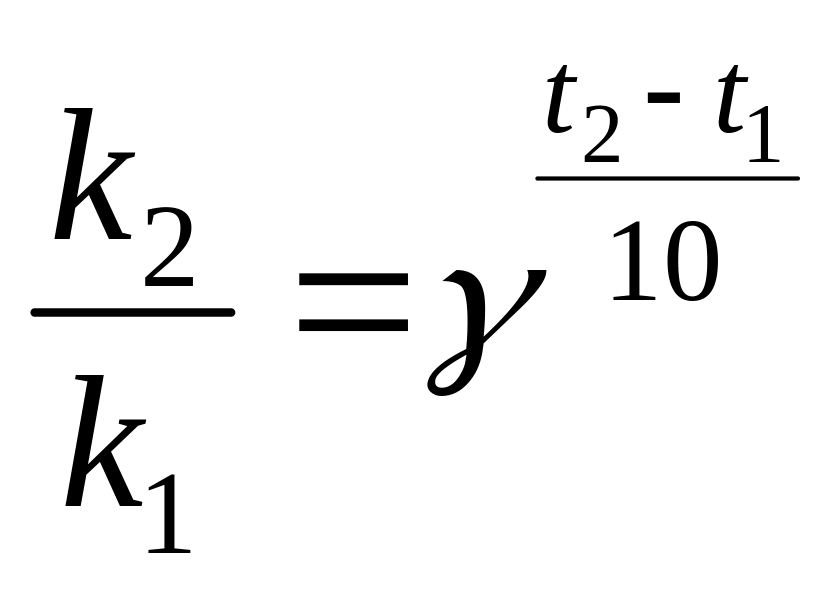
в) рассчитываем, подставляя полученное значение в уравнения (21):

1. 

или

2. 

Ответ: при °С.

Пример 8. На сколько градусов надо повысить температуру реакции, чтобы скорость ее увеличилась в 15 раз, если .

Решение. Из математического выражения правила Вант-Гоффа (16) и условия задачи получаем:

, откуда

(22)

Логарифмируя уравнение (22), получаем формулу для определения :

(23)

Подставляя в (23) условия задачи, получаем:

°

Ответ: Температуру реакции надо повысить на 7,78 °.

Примечание: Если известна температура ( ), при которой проводилась реакция ранее, то используя полученные данные, можно рассчитать температуру ( ), при которой следует проводить реакцию, чтобы скорость ее увеличилась в N раз:

.

Пример 9. Сколько времени потребуется для проведения реакции при температуре 348 °К, если при температуре 298 °К она заканчивается за 30 минут; .

Решение

1. Из правила Вант-Гоффа (16) следует:

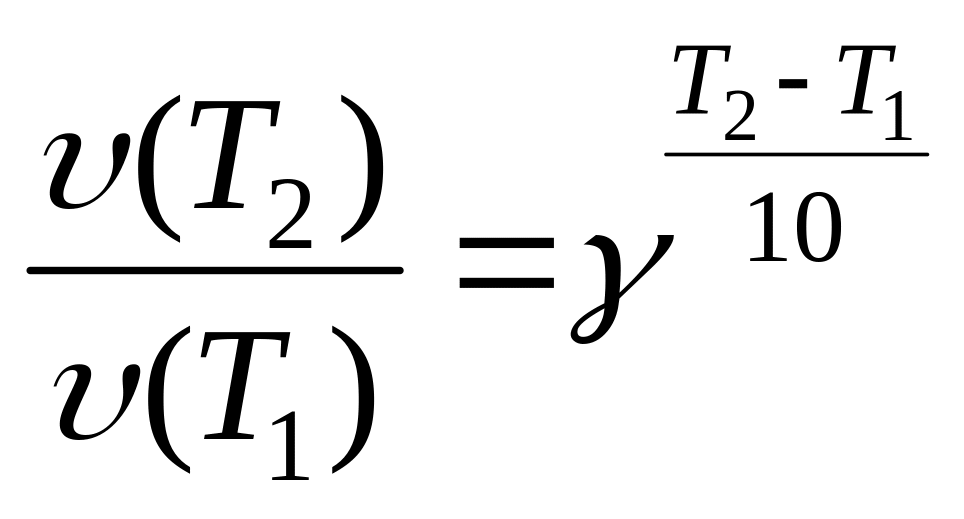(24)

2. Поскольку скорость реакции обратно пропорциональна времени (1, 4), то

(25)

3. Из (24), (25) получаем:

,

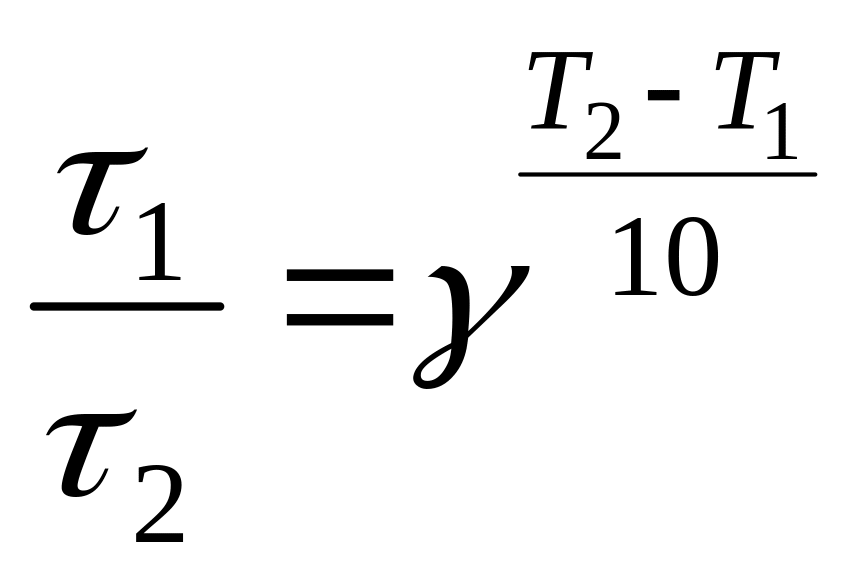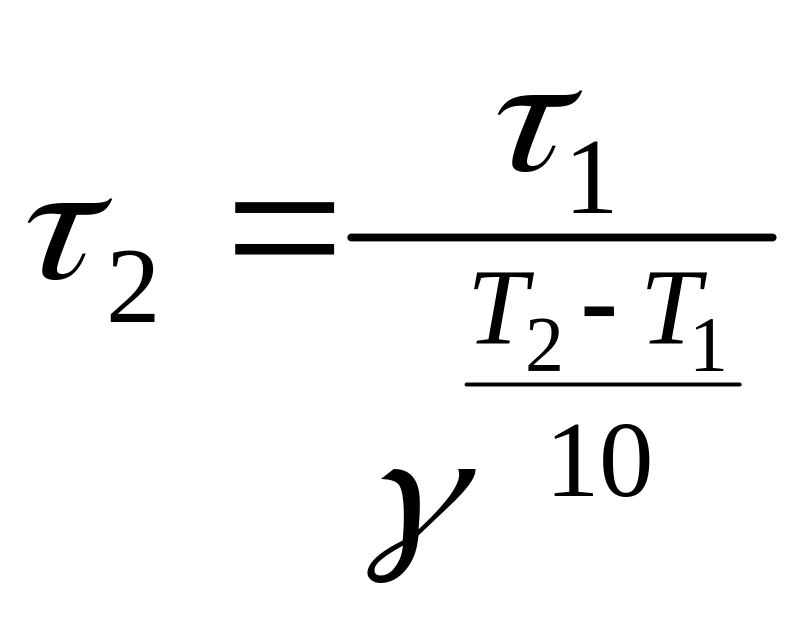
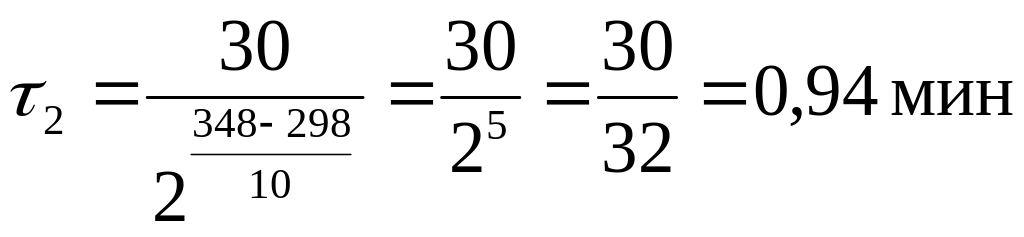
Таким образом, при К реакция закончится за 0,94мин.

0. Уравнение Аррениуса

Более точно зависимость константы скорости реакции от температуры описывается уравнением Аррениуса:

, (26)

Если при изменении температуры концентрация реагентов остается постоянной, то зависимость скорости реакции от температуры описывается уравнением:

, где (27)

- основание натурального логарифма;

- энергия активации реакции, Дж/моль;

- универсальная газовая постоянная, Дж/моль·К;

- температура, К;

- предэкспоненциальный множитель;

при .

Энергия активации – это минимальная дополнительная или избыточная энергия по сравнению со средней энергией реагирующих частиц, которой должны обладать соударяющиеся частицы, чтобы вступить в реакцию. Частицы, обладающие такой энергией, называются активными. Энергия активации процесса зависит от природы реагирующих веществ. Значения энергии активации для химических реакций могут составлять от 40 до 200 кДж/моль. По гипотезе Аррениуса химическое взаимодействие осуществляется только при соударении активных частиц, доля которых в системе пропорциональна величине . С увеличением температуры доля этих частиц в системе растет и соответственно растет скорость реакции.

Используя уравнение Аррениуса можно рассчитать:

• и реакции, если известны константы скорости реакции при двух температурах;

• константу скорости реакции при заданной температуре, если известны энергия активации реакции и константа скорости при какой-либо температуре.

Скорости при нескольких температурах можно рассчитать двумя способами.

Пример 10. Рассчитайте энергию активации процесса, если известно:

, К	726	746	766
, с-1	0,0103	0,02447	0,05803

Решение. рассчитываем, используя уравнение Аррениуса (26) для двух температур:

и

Откуда:

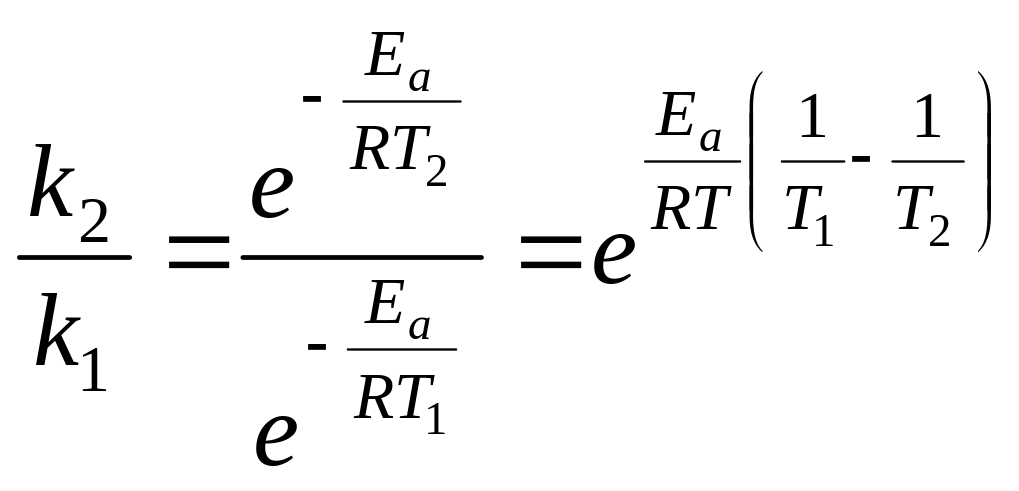
Прологарифмировав последнее уравнение, с учетом того, что получаем:

и, соответственно:

Для 726 К и 746 К:

Дж/моль.

Для 726 К и 766 К:

Дж/моль.

Для 746 К и 766 К:

Дж/моль.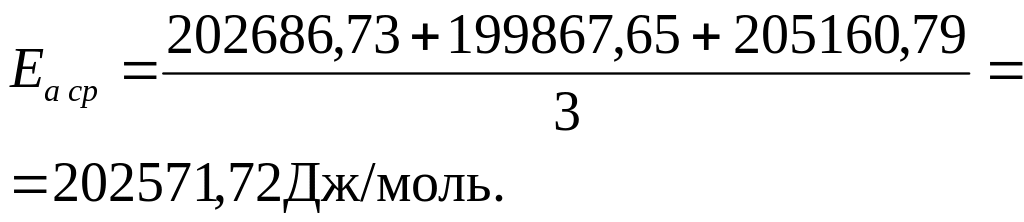

Средняя энергия активации равна кДж/моль.

Пример 11. Рассчитайте и процесса, если известны константы скоростей реакции при различных температурах.

, К	283	303	313
, л·моль-1·мин-1	2,43	10,53	21,9

Решение. , определяем графическим методом, используя логарифмическую форму уравнения Аррениуса (26):

(28)

Для этого представим экспериментальные данные в следующем виде:

	3,53	3,30	3,19
	0,38	1,02	1,34

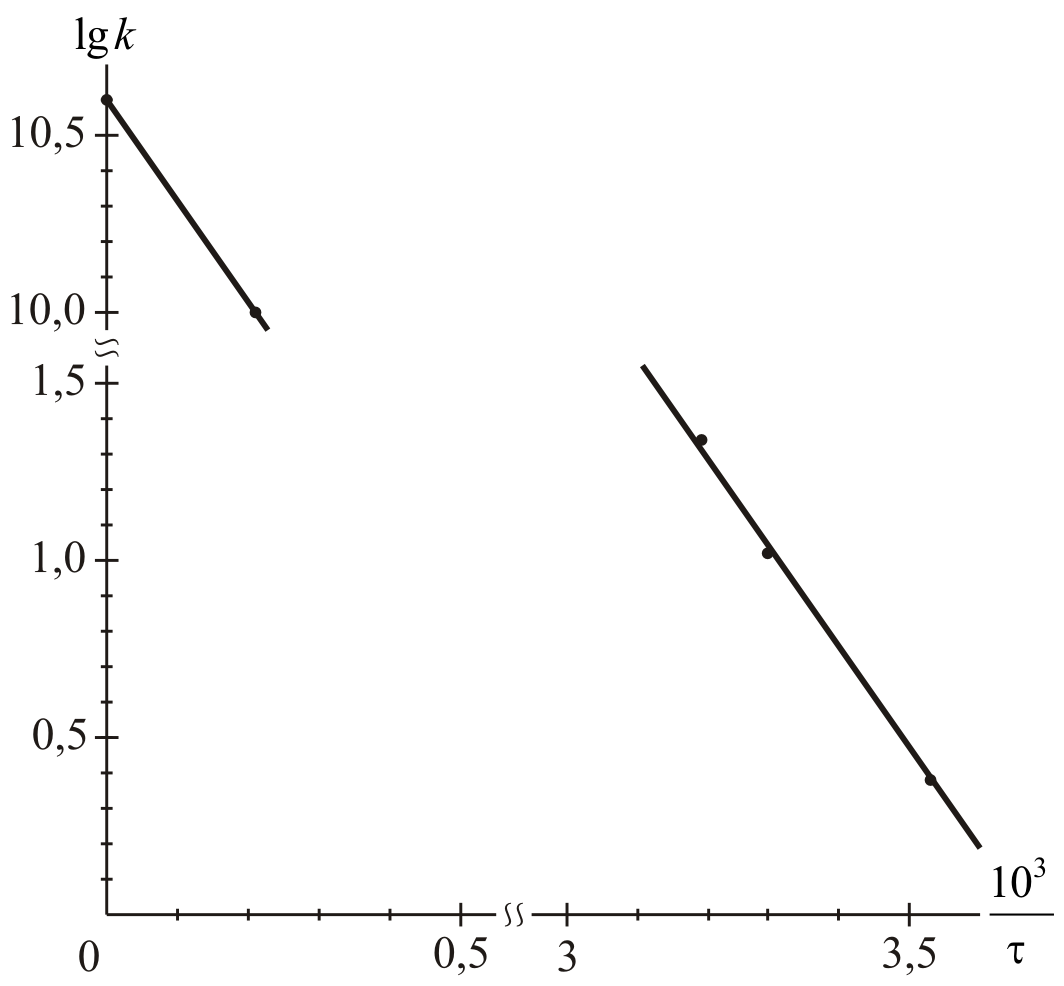
На их основе строим график зависимости от (см. рис. 1).

Из рис.1, согласно уравнению (26)

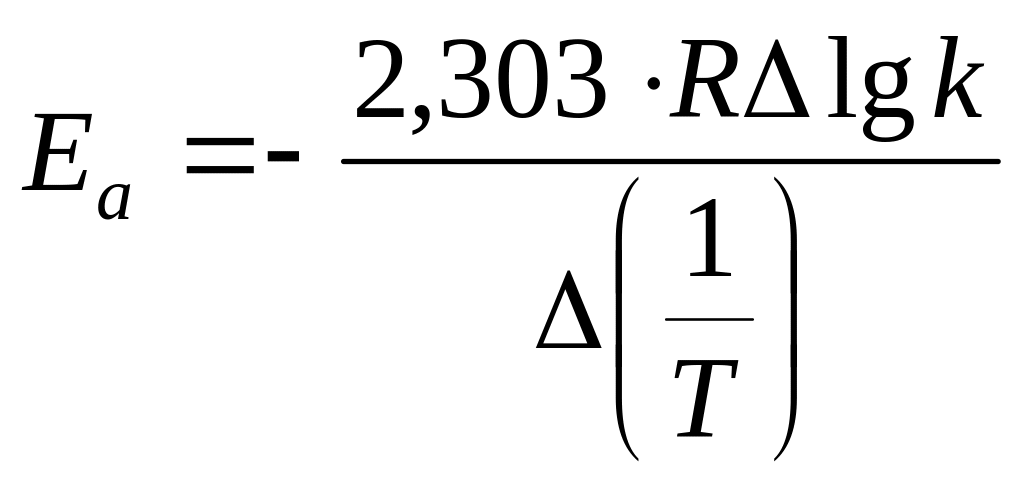
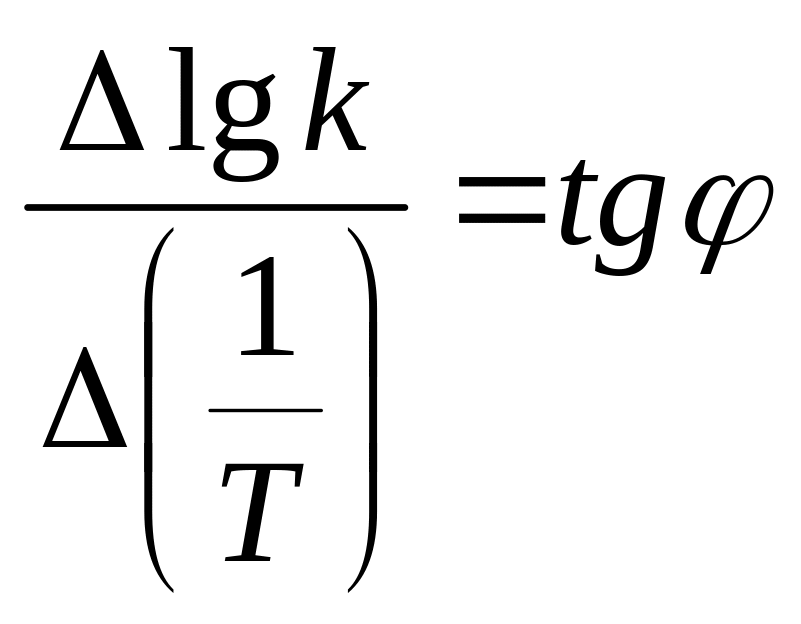находим из графика:

Дж/моль.

Из уравнения (24) следует:

. .

Продлив график до пересечения с осью , получаем

.

Таким образом: Дж/моль, .

Приложение 1

Федеральное агентство по образованию Новосибирский государственный архитектурно-строительный университет Кафедра химии Индивидуальное задание по химии Работу выполнил студент: ______________________ группа_____ «___»____________2009 г. Работу проверил преподаватель: ________________________ «___»____________2009 г. Новосибирск 2009

27