- •Белорусский государственный университет
- •Исходные данные приведены в табл. 1
- •Выразим к через параметр т2.
- •Для получения уравнений состояний в нормальной форме используем дифференциальное уравнение замкнутой системы
- •Таким образом, исходная система не удовлетворяет заданным показателям качества, ее следует скорректировать.
- •Учет требований качества переходного процесса: tnn и σ, запасов устойчивости учитываются при формировании среднечастотной области Lж(ω). Здесь можно воспользоваться графиком (рис. 1.6).
- •Корректирующему звену соответствует функция :
- •Для нахождения переходных характеристик замкнутой системы с корректирующим звеном предварительно сформируем модель в пространстве состояний. Передаточная функция замкнутой системы имеет вид:
- •II исследование линейных импульсных сау
- •На рис.2.5 представлена диаграмма Боде исследуемой дискретно системы, с отмеченными на ней запасами устойчивости по амплитуде и фазе.
- •III исследование нелинейной непрерывной системы автоматического управления
- •Литература
II исследование линейных импульсных сау
Исходные данные:
Таблица 2
|
Номер варианта |
γ |
Т |
T1 |
τ1 |
|
26 |
1 |
0,5 |
0,5 |
0,1 |
Анализируется одноконтурная замкнутая импульсная САУ, составляющая из непрерывной части (НЧ) и импульсного элемента (ИЭ), формирующего прямоугольные импульсы длительностью τ=γТ, где Т -период дискретизации, 0≤γ≤1. Исходные данные для расчетов приведены в табл. 2. Для всех вариантов заданий передаточная функция непрерывной части имеет вид
 .
(1.1)
.
(1.1)
Импульсный элемент представляется в виде идеального ключа и формирующего устройства с передаточной функцией
 (1.2)
(1.2)
Структурная схема системы представлена на рис. 2.1. В табл. 2 Т, Т1, τ1 -постоянные времени имеют размерность секунды, К0 - коэффициент передачи
НЧ имеет размерность сек-1 и выбирается далее.

Рис 2.1 Структурная схема линейной импульсной системы
1.
Для нахождения передаточной функции
разомкнутой импульсной САУ W(z),
представим
 в виде суммы двух слагаемых:
в виде суммы двух слагаемых:
 (1.3)
(1.3)
где
 ,
, .
.
Таблица 2.1
|
|
|
|
|
|
|
|
|
|
Воспользуемся табл. 2.1, тогда:
 ,
,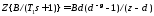 . (1.4)
. (1.4)
Таким образом:
 . (1.5)
. (1.5)
Теперь воспользуемся формулой:
 .
(1.6)
.
(1.6)
Найдем:
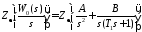 . (1.7)
. (1.7)
По таблицам Z–преобразования [6] находим:
 , (1.8)
, (1.8)
 . (1.9)
. (1.9)
Таким образом, имеем
 , (1.10)
, (1.10)
откуда
находим
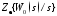 при
при и
и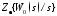 при
при и подставляем их в [5, (1.18)]. После
преобразований приходим к выражению
[5, (1.19)]. Как и следовало ожидать, оба
способа дали одинаковую передаточную
функцию, которую можно записать и так
и подставляем их в [5, (1.18)]. После
преобразований приходим к выражению
[5, (1.19)]. Как и следовало ожидать, оба
способа дали одинаковую передаточную
функцию, которую можно записать и так
 , (1.11)
, (1.11)
где
 ,
, ,K
= K0(τ1s
+ 1), α=
1/T1.,
,K
= K0(τ1s
+ 1), α=
1/T1., ,
, ,
, ,
, а
коэффициенты
а
коэффициенты и
и определены выше.
определены выше.
Передаточные функции замкнутой системы легко находятся по выражениям
 (1.12-1.13)
(1.12-1.13)
 (1.14)
(1.14)
где
 (1.15)
(1.15)
 (1.16)
(1.16)
2.
Устойчивость
системы определяется корнями
характеристического уравнения замкнутой
системы
 ,
которое для
нашего случая будет иметь вид:
,
которое для
нашего случая будет иметь вид:
a0z2 +(a1+ c0)z +a2 +c1= z2+b1z + b2 =0.
В соответствии c алгебраическим критерием [6, с. 432] замкнутая система будет устойчива при выполнении неравенств:

В неравенстве при известных значениях γ, Т, τ1, Т1 входит величина К0. Таким образом, можно выделить отрезок значений К0’’<К0 <К0’ при которых система будет устойчива и далее принять К0 = 0,5К'0. Условия устойчивости будут:
 (1.17)
(1.17)
 (1.18)
(1.18)
 (1.19)
(1.19)
После преобразований и возврата к старым переменным получим:



Вычислим эти значения. Получим 0<К0<1.14. Таким образом, принимаем К0=0.5K’0 =0.57.
3. Для построения частотных и логарифмических частотных характеристик в выражении W* (z) делаем замену переменной

В результате этого получим частотную характеристику Ww*(jω*) и далее логарифмическую амплитудно-частотную характеристику
L*( ω*) = 20lg |W*(jω*)| и фазочастотную характеристику φ*(ω*)=argWw*(jω*), графики, которых строятся в логарифмическом масштабе.
Передаточная функция разомкнутой системы имеет вид:
 (1.21)
(1.21)
тогда можно воспользоваться следующей последовательностью команд Matlab:
Ts=T*γ
>> sys=tf([c0 c1],[a0 a1 a2],Ts)
0.1 z + 0.075
---------------------
z^2 - 1.368 z + 0.368
Sampling time: 0.5
>> sys_tr=d2c(sys,'tustin') (опция 'tustinпредназначена для преобразования (1.20))
-0.009137 s^2 - 0.2193s+ 1.023
--------------------------------
s^2 + 1.848s- 8.207e-016
Получаем выражение:
 (1.22)
(1.22)
где параметры g и f видны из вышеприведенного выражения.

Рис.2.2
4. Рассматриваемая система для всех вариантов является астатической с астатизмом первого порядка и имеет следующую передаточную функцию
 (1.23)
(1.23)
где
 = (c0z
+ c1)/(z-d).
= (c0z
+ c1)/(z-d).
В
силу астатизма первого порядка в такой
системе статическая ошибка всегда равна
нулю, а скоростная еск
вычисляется
по формуле eCK=1/ .
.
Тогда:
 (1.24)
(1.24)
и следовательно, еск= 3.612.
Вычислим коэффициенты ошибок. Величина С0 =0, а коэффиц3иент ошибки С1, находится по следующей формуле
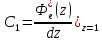 (1.25)
(1.25)
где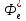 (z)
- передаточная функция системы по ошибке.
Она ровна:
(z)
- передаточная функция системы по ошибке.
Она ровна:
>> sys_e=1/(1+sys_tr)
Transfer function:
s^2 + 1.848 s - 8.207e-016
----------------------------
0.9909 s^2 + 1.629 s + 1.023
Посчитали производную в MathCad и подставив s=1, получили С1 = 10.705.

Рис. 2.3
5. При входном воздействии вида v(k) = l[k] переходный процесс в замкнутой системе можно вычислить с помощью моделирования импульсной системы в Matlab. Для этого необходимо задать передаточную функцию непрерывной части системы в tf- или zpk -форме, преобразовать ее в дискретную с помощью оператора c2d при заданном времени дискретизации Г, а затем построить переходной процесс системы оператором step. Так же можно построить и логарифмические частотные характеристики импульсной системы – bode. Если задана передаточная функция замкнутой системы в виде
 и
период дискретизации γT,
то получим рис.2.4.
и
период дискретизации γT,
то получим рис.2.4.
w0=tf([t1 1 0],[t1 1 K0*(tay+1)])
w1=c2d(w0,Ts)
Transfer function:
0.5 s^2 + s
-------------------
0.5 s^2 + s + 0.627
Transfer function:
z^2 - 1.287 z + 0.2873
----------------------
z^2 - 1.175 z + 0.3679
Samplingtime: 0.5