Таким образом, исходная система не удовлетворяет заданным показателям качества, ее следует скорректировать.

5. Если исходная система не удовлетворяет заданным показателям качества, ее следует скорректировать. В случае применения частотных методов синтеза коррекции строится желаемая ЛAЧX L_ж(ω). В низкочастотной части желаемой ЛАЧХ при сохранении порядка астатизма (наличие интегратора 1/s в системе)

Требуемый коэффициент усиления выбирается из соотношения K_υ≥v₁/e_ск = 2.4 / 0.07 = 34.29 На частоте среза желательно иметь наклон ЛАЧХ -20 дБ/дек с протяженностью этого участка не менее одной декады. Далее среднечастотная часть ЛАЧХ сопрягается с низкочастотной отрезком прямой с наклоном -40(если необходимо -60) дБ/дек, а высокочастотная часть желаемой исходной ЛАЧХ по возможности должны совпадать.

Учет требований качества переходного процесса: tnn и σ, запасов устойчивости учитываются при формировании среднечастотной области Lж(ω). Здесь можно воспользоваться графиком (рис. 1.6).

Рис. 1.6

По графику рис. 1.6 для заданных значений 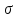иt_nn находят ω_n, и затем из соотношения ω_c = (0.6 ÷ 0.9) ω_n частоту среза ω_c. В нашем случае: (как показано на рис.1.6,а) для 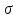=25%,t_p ≈, откуда для t_p , значение ω_n= и ω_c =7.533

Сопряжение среднечастотного участка с низкочастотным и высокочастотным (рис. 1.7) должно быть таким, чтобы была проще коррекция и чтобы изломы, по возможности, были не более чем на 20 (протяженность участка около декады). Тогда, выберемL₂=20дб на частоте ω₂=(0.1-0.5) ω_с =0.4∙ω_с=3.348<ω_с=7.533 и L₃=-20 дб на частоте ω₃=33.5 > ω_с=7.533. А ω₁=. Введем обозначения:

Корректирующему звену соответствует функция :

(1.9)

Где,

Общая передаточная функция разомкнутой системы с корректирующим звеном последовательного типа имеет вид:(1.10)

где (1.11)

Далее воспользуемся функцией zpk(z, р, Кd), где z и р - векторы из нулей и полюсов, a Kd - обобщенный коэффициент передачи, sys - любое имя присваиваемое модели. Тогда запись в системе Matlab примет вид:

sys1=zpk([-1/T2k -1/T3k],[0 -1/T1 -1/T2 -1/T3 -1/T1k -1/T4k],Kd) Результат представления sysl представлен ниже.

Zero/pole/gain:

704 (s+3.348) (s+10)

------------------------------------------

s(s+21.28) (s+33.5) (s+10) (s+2.87) (s+1)

Диаграммы Боде (margin(sysl)) представлены на рис. 1.8. На диаграмме также обозначены запасы устойчивости, которые являются приемлемыми.

Рис.1.8

Для нахождения переходных характеристик замкнутой системы с корректирующим звеном предварительно сформируем модель в пространстве состояний. Передаточная функция замкнутой системы имеет вид:

(1.12)

Для нахождения Ф(s) воспользуемся следующей последовательностью команд sysl=zpk([-l/T2k -1/T3k],[0 -1/Т1 -1/T2 -1/T3 -1/T1k -l/T4k],Kd) Zam_ck=inv(l+sysl)*sysl - находится передаточная функция замкнутой системы. (Не оптимальная форма т.к. при такой последовательности команд не производится упрощение за счет сокращения одинаковых элементов числителя и знаменателя. В тоже время на результат дальнейшего расчета это не влияет)

704 s (s+21.28) (s+33.5) (s+10)^2 (s+3.348) (s+2.87) (s+1)

---------------------------------------------------------------------------------------------------

s (s+33.45) (s+33.5) (s+21.41) (s+21.28) (s+10)^2 (s+2.955) (s+2.87) (s+1) (s^2 + 0.8372s + 1.114)

Переходная характеристика (рис. 1.9 ) находится с помощью функций: sys3=ss(Zam_ck); step(sys3). Из рассмотрения рис. 1.9 видно, что параметры по заданию выполняются.

Рис. 1.9

Для устранения неоптимальности записи в Zam_ck=inv(l+sysl)*sysl можно в диалоговом режиме произвести новую запись zpk(.) - сокращая одинаковые элементы числителя и знаменателя в Zam_ck.