4.4 Примеры аудиторных и домашних заданий
Задание 1.
Определить мощность множества двоичных
слов (интерпретаций), на которых определена
булева функция
.
Решение.
Количество
аргументов заданной булевой функции
равно 6 (
).
Мощность множества двоичных слов, на
которых определена булева функция
,
вычисляется по формуле
.
Всего двоичных слов (интерпретаций), на
которых определена булева функция
,
будет
слова.
Задание 2. Определить количество булевых функций, которые зависят от 5-ти переменных.
Решение.
Число всех функций,
зависящих от
переменных, равно
,
следовательно, число всех функций,
зависящих от 5-ти переменных
,
равно
.
Задание 3.
Построить таблицу
истинности функции
и определить её порядковый номер.
Решение. Построим
таблицу истинности функции (таблица
4.16), введя дополнительные обозначения
(
и
)).
Таблица 4.16 Таблица истинности функции
-
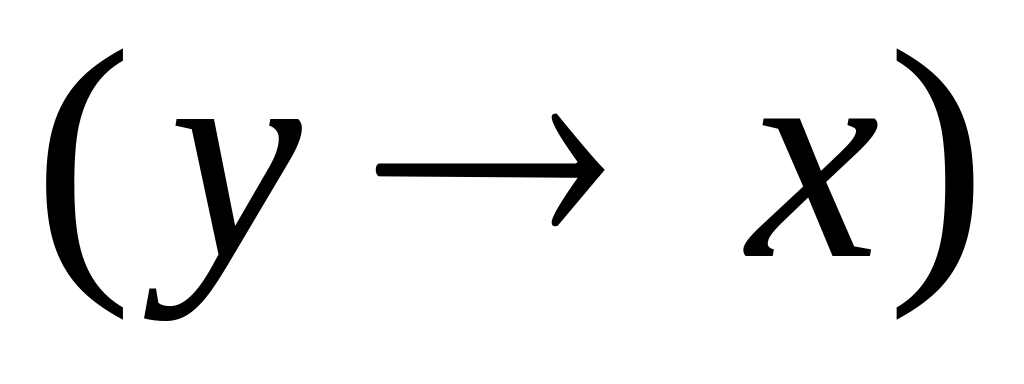
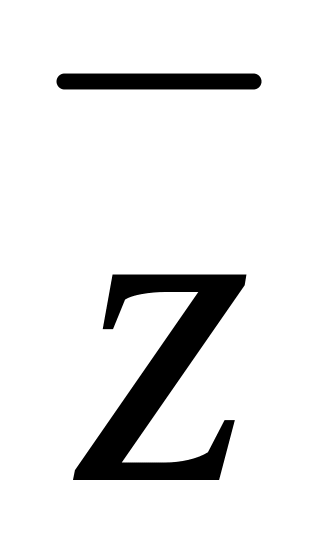
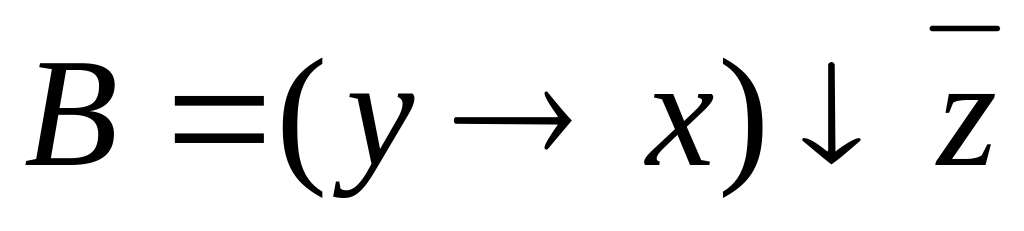
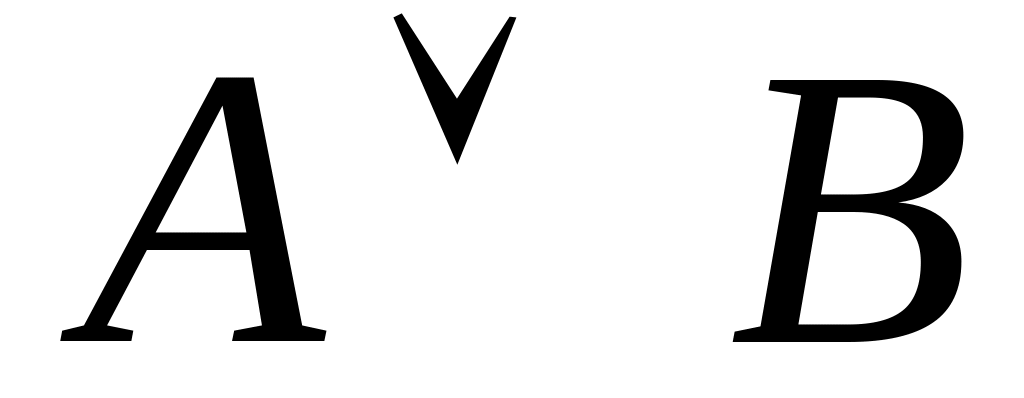
0
0
0
1
1
1
0
1
0
0
1
1
1
0
0
1
0
1
0
0
0
1
0
0
0
1
1
0
0
0
1
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
0
0
1
1
0
1
1
1
0
1
1
1
1
1
1
0
0
1
Двоичный код, соответствующий значениям этой функции, равен 11010011 (последний столбец таблицы).
Переведем двоичное
число
в десятичную систему счисления:
.
Порядковый номер
функции равен
.
Задание 4.
Построить таблицу
истинности для бинарной функции
с порядковым номером 14.
Решение.
Найдем двоичное
число, соответствующее десятичному
числу 14, представив это число как сумму
степеней числа 2, т.е.
.
Таким образом,
соответствует двоичному числу
.
Построим искомую таблицу истинности (см. таблицу 3.30), поместив полученное число в столбце значения функции таким образом, чтобы младший разряд оказался в нижней строке.
Таблица 3.30 Таблица истинности функции
-
0
0
1
0
1
1
1
0
1
1
1
0
Задание 5.
Эквивалентны ли формулы
и
,
если
,
а
?
Решение. Построим таблицы истинности для формул (см. таблицу 3.29) и (таблица 4.17). Проверим эквивалентность формул с помощью таблиц реализуемых ими функций (таблица 3.31).
Таблица 4.17 Обобщенная таблица истинности функций, реализуемых формулами и
-
0
0
0
1
1
0
0
1
0
0
0
1
0
1
0
0
1
1
0
1
1
0
0
0
1
1
0
1
1
1
1
1
0
0
1
1
1
1
1
1
Так как таблицы истинности функций не совпадают (столбцы и ), следовательно, формулы неэквивалентны.
Задание 6.
Проверить, справедливы ли следующие отношения:
а)
;
б)
.
Решение.
а) с помощью
эквивалентных преобразований преобразуем
правую и левую часть отношения
.
Сначала преобразуем левую часть:
.
Так как левая и правая часть отношения оказались равными, следовательно, отношение справедливо.
б) преобразуем левую часть отношения:
;
преобразуем правую часть отношения:
.
Получаем
.
Это можно проверить с помощью таблицы
истинности (таблица 4.18), обозначив
,
.
Таблица 4.18
Таблица истинности функций
и
-
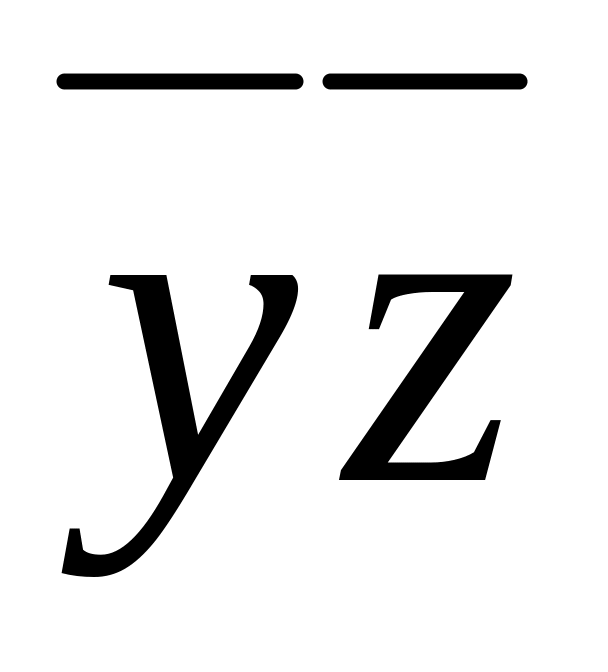
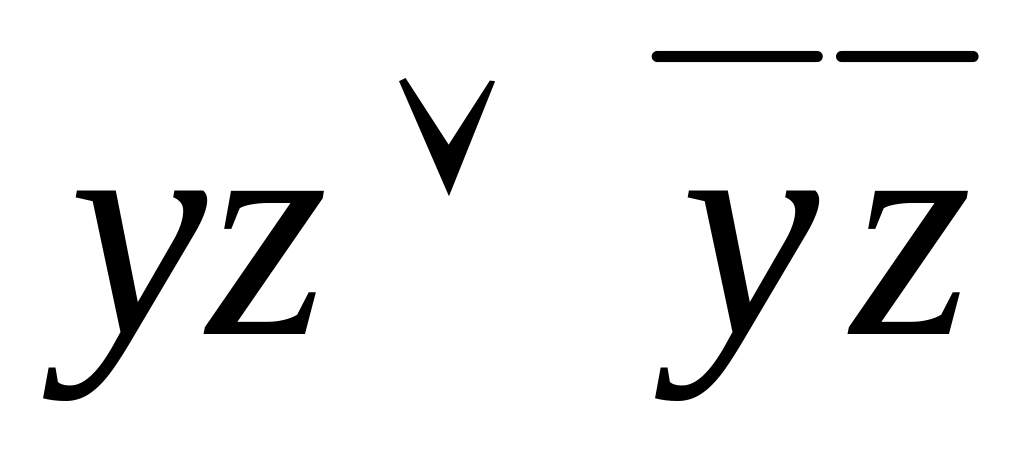
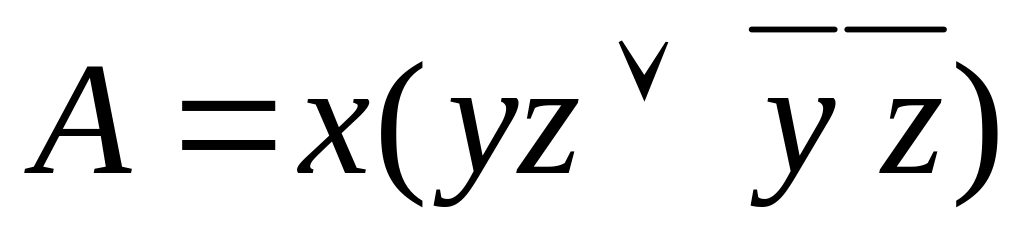
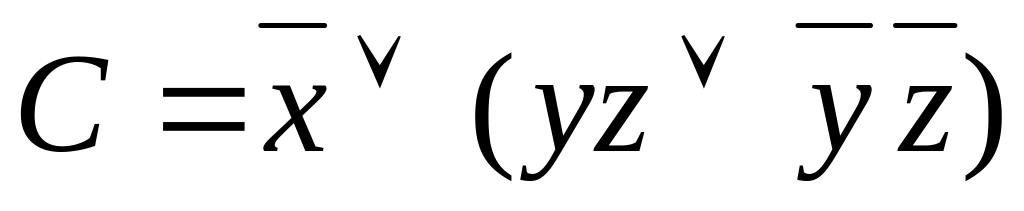
0
0
0
0
1
1
0
1
0
0
1
0
1
0
0
1
0
1
0
0
0
0
0
1
0
1
1
1
0
1
0
1
1
0
0
0
1
1
1
1
1
0
1
0
1
0
0
0
1
1
0
0
1
0
0
0
1
1
1
1
1
1
1
1
Столбцы и не равны, следовательно, отношение несправедливо.
Задание 7.
Найти функцию,
двойственную функции
,
если известно, что
только на интерпретациях (001), (011), (111).
Решение.
Построим таблицу
истинности функции
(таблица 4.19). Для столбца значений функции
генерируем набор противоположных
(инверсных) значений (10101110). Записав его
в обратной последовательности, получим,
таким образом, столбец значений
двойственной функции
.
Таблица 4.19– Таблица истинности двойственных функций
-
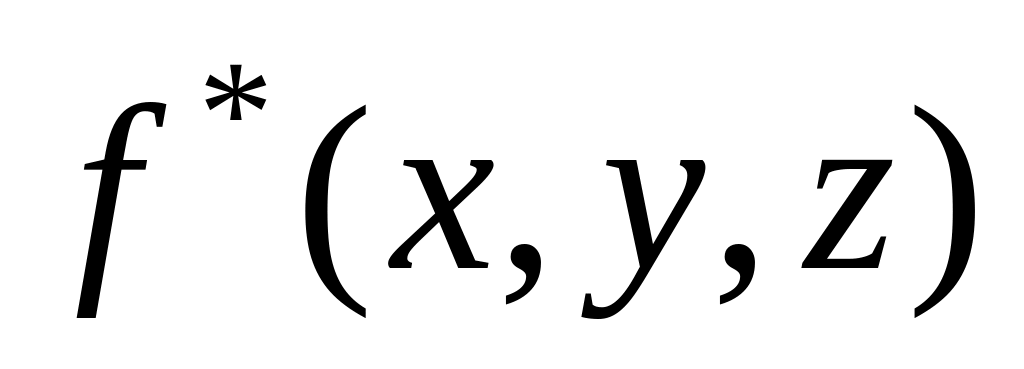
0
0
0
0
0
0
0
1
1
1
0
1
0
0
1
0
1
1
1
1
1
0
0
0
0
1
0
1
0
1
1
1
0
0
0
1
1
1
1
1
Задание 8.
Найти функцию, двойственную функции
.