4.2.2.6 Булевы алгебры. Законы и тождества булевой алгебры.
Определение.
Алгебраическая
структура
,
где
и операция
есть конъюнкция
,
есть дизъюнкция
(таблица 3.4), «
»
есть отрицание
(таблица 3.2), называется двухэлементной
булевой алгеброй.
Определение.
Алгеброй логики
называется двухэлементная булева
алгебра
,
где носитель алгебры
,
и в которой множество операций дополнено
двумя бинарными операциями: импликацией
и эквивалентностью
(см. таблицу 3.4).
На основе определения основных операций (отрицание, дизъюнкция, конъюнкция) нетрудно убедиться в справедливости следующих законов (свойств) булевой алгебры.
Рассмотрим основные законы (свойства) булевой алгебры.
Закон коммутативности (переместительный закон)
;
.
Пример.
Доказать коммутативность операции дизъюнкции можно, используя таблицы истинности (таблица 4.7).
Таблица 4.7 Таблица истинности для доказательства коммутативности операции дизъюнкции
-
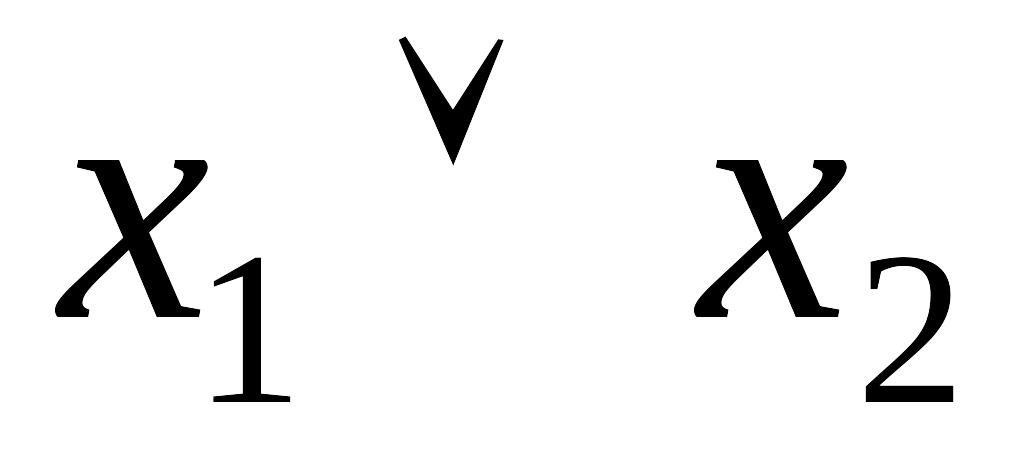
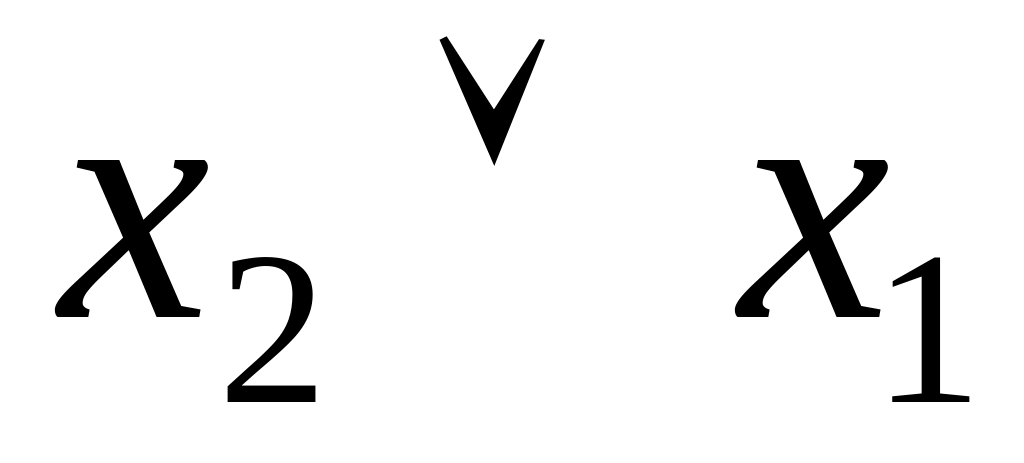
0
0
0
0
0
1
1
1
1
0
1
1
1
1
1
1
Столбцы и в таблицах истинности содержат одинаковые значения, что доказывает коммутативность операции дизъюнкции.
Найдем тождество,
двойственное данному, для чего заменим
все функции на двойственные им
,
.
Закон ассоциативности (сочетательный закон)
;
.
Пример.
Доказать ассоциативность операции конъюнкции можно, используя таблицы истинности (таблица 4.8).
Таблица 4.8 Таблица истинности для доказательства ассоциативности операции конъюнкции
-
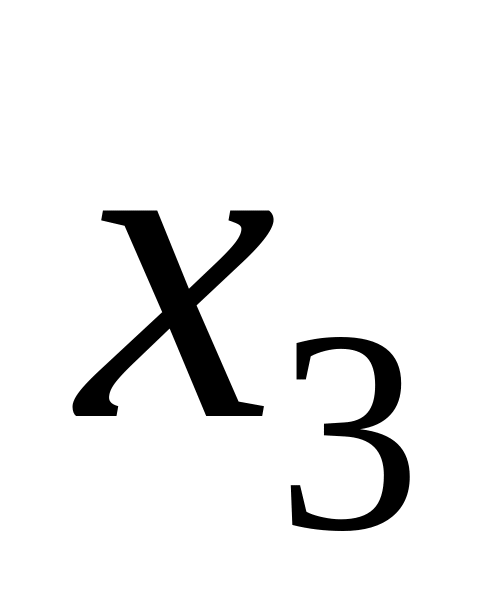
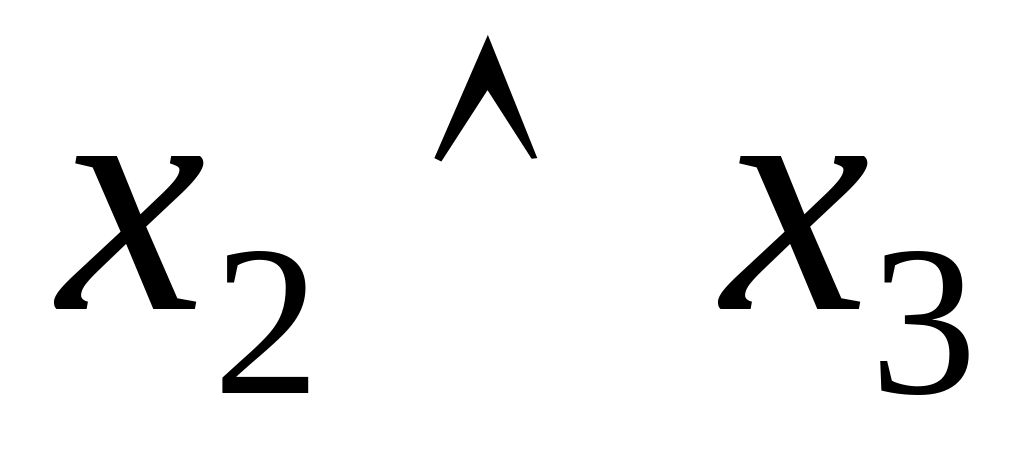
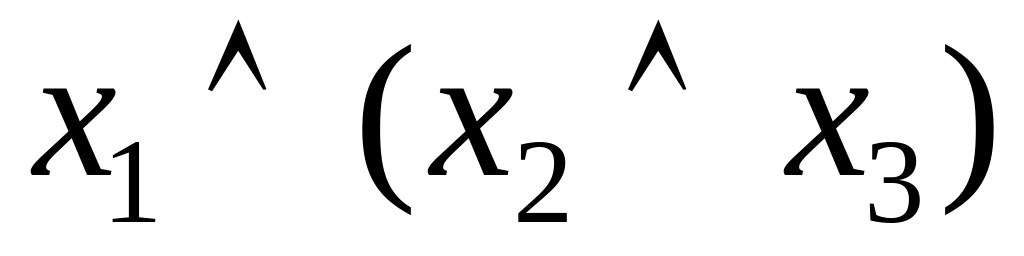
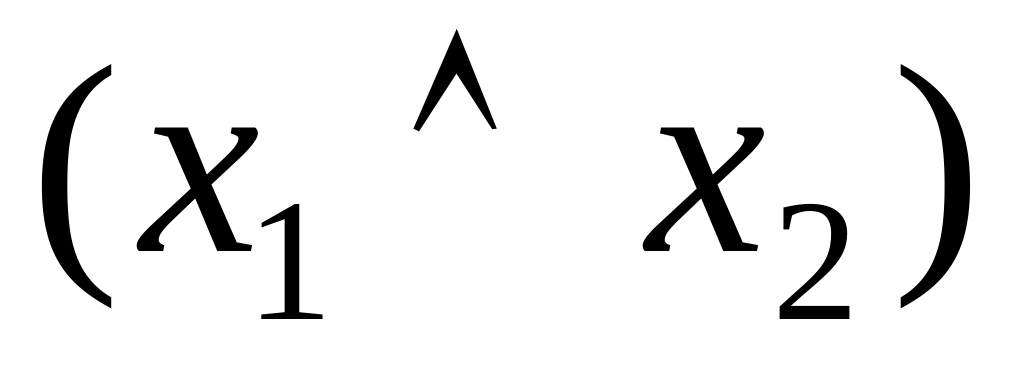
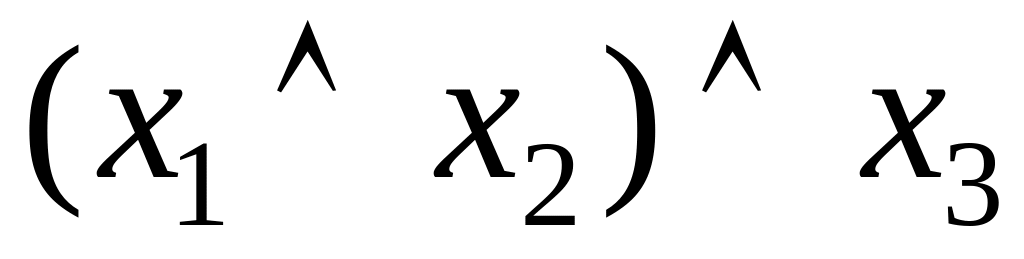
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
0
1
1
1
0
0
0
1
0
0
0
0
0
0
1
0
1
0
0
0
0
1
1
0
0
0
1
0
1
1
1
1
1
1
1
Столбцы, соответствующие левой и правой частям второго равенства, содержат одинаковые значения, что доказывает справедливость тождества .
Тождество, выражающее ассоциативность дизъюнкции, двойственно доказанному, так как может быть получено из него путем замены всех функций на двойственные им, и, следовательно, оно тоже верно.
Закон дистрибутивности (распределительный закон)
;
.
Пример.
Доказательство дистрибутивности конъюнкции относительно дизъюнкции можно провести, используя таблицы истинности (таблица 4.9).
Таблица 4.9 Дистрибутивность конъюнкции относительно дизъюнкции
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Столбцы, соответствующие левой и правой частям первого равенства, содержат одинаковые значения, что и доказывает справедливость равенства . Двойственное тождество выражает дистрибутивность дизъюнкции относительно конъюнкции.
Закон идемпотентности
;
.
Пример.
Для доказательства закона идемпотентности используем таблицу истинности (таблица 4.10).
Таблица 4.10 Закон идемпотентности
-
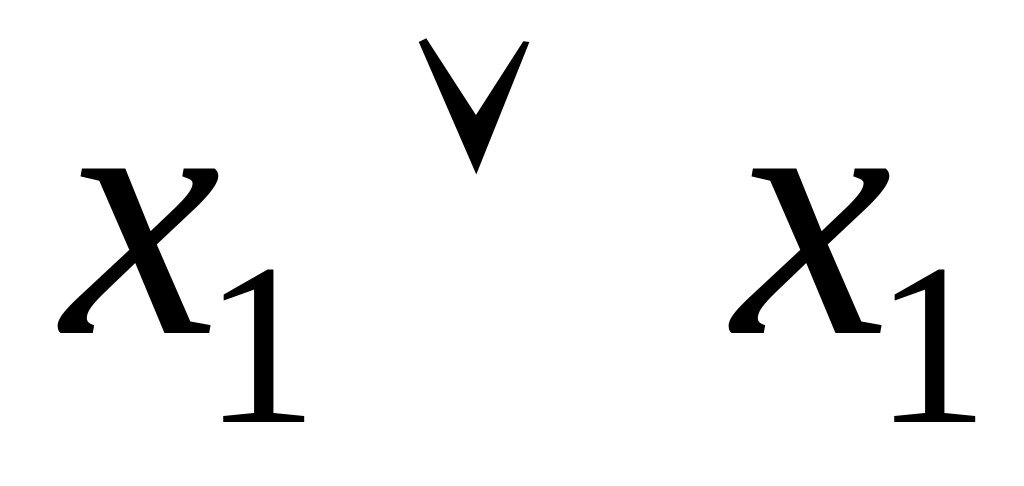
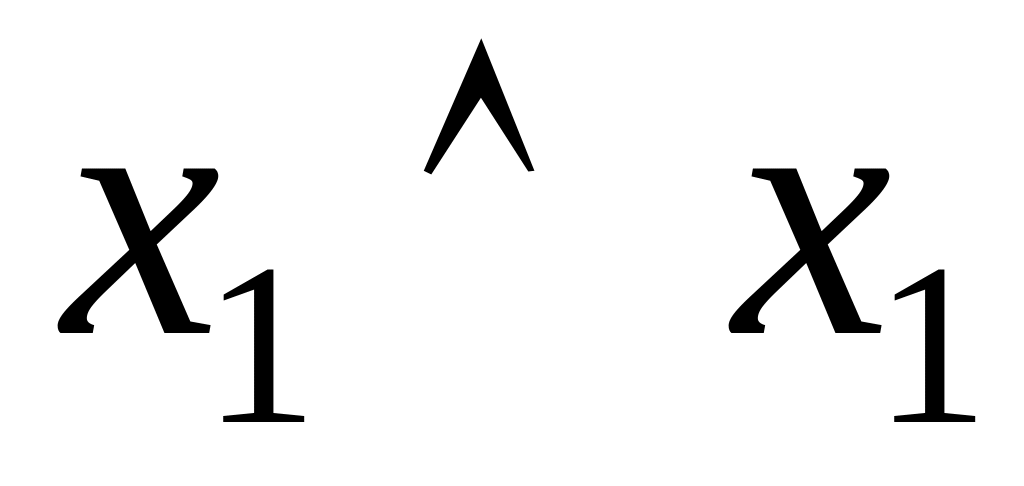
0
0
0
1
1
1
В таблице значения всех столбцов одинаковы и совпадают со значением переменной , что и доказывает оба тождества. Данные тождества являются двойственными друг другу.
Закон исключенного третьего
.
Пример.
Для доказательства закона исключенного третьего используем таблицу истинности (таблица 4.11).
Таблица 4.11 Закон исключенного третьего
-
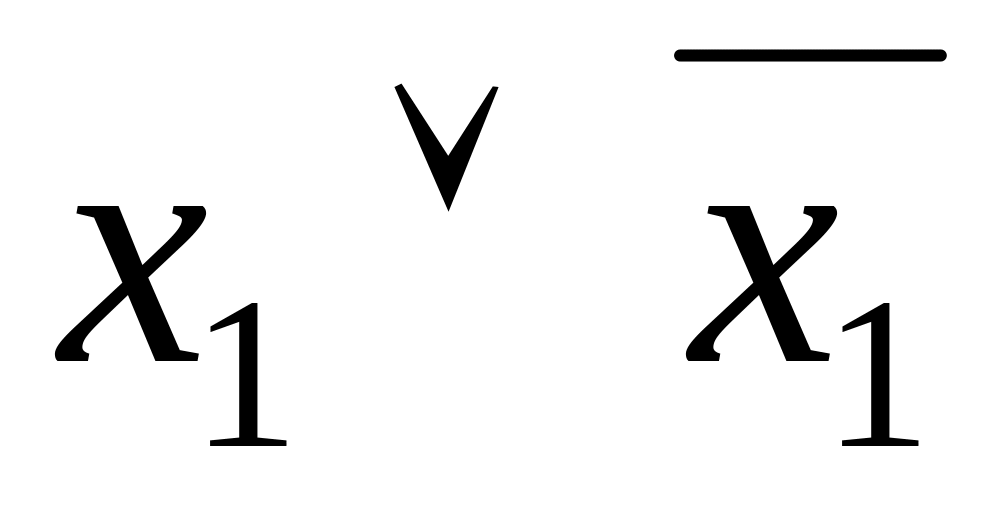
0
1
1
1
0
1
Столбец истинности, представляющий левую часть доказываемого тождества, равен константе единицы, что и требовалось доказать.
Закон противоречия
.
Пример.
Для доказательства закона противоречия используем таблицу истинности (таблица 4.12).
Таблица 4.12 Закон противоречия
-
0
1
0
1
0
0
Данный закон является двойственным к доказанному выше закону исключенного третьего.
Закон тождества (свойство констант)
;
;
;
.
Пример.
Для доказательства закона тождества (свойство констант) используем таблицу истинности (таблица 4.13).
Таблица 4.13 Таблицы истинности тождеств
-
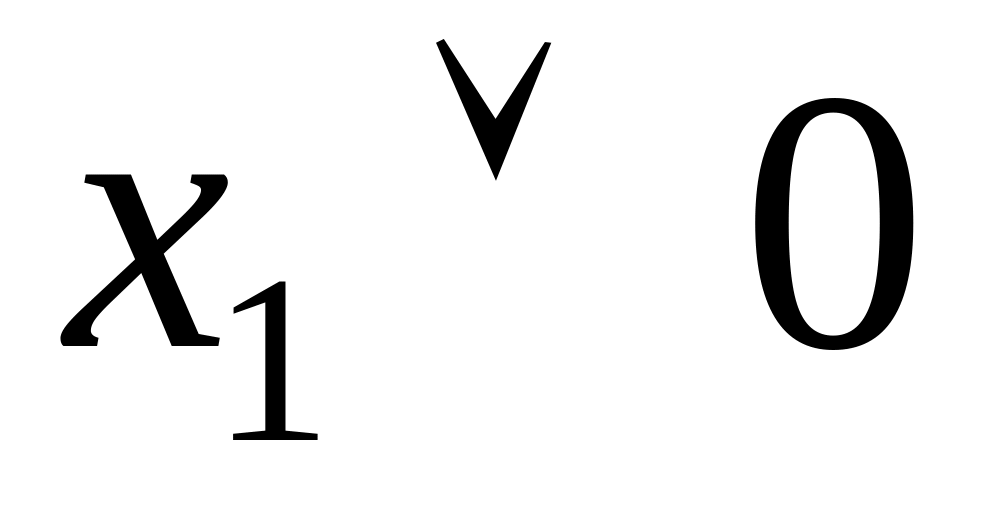
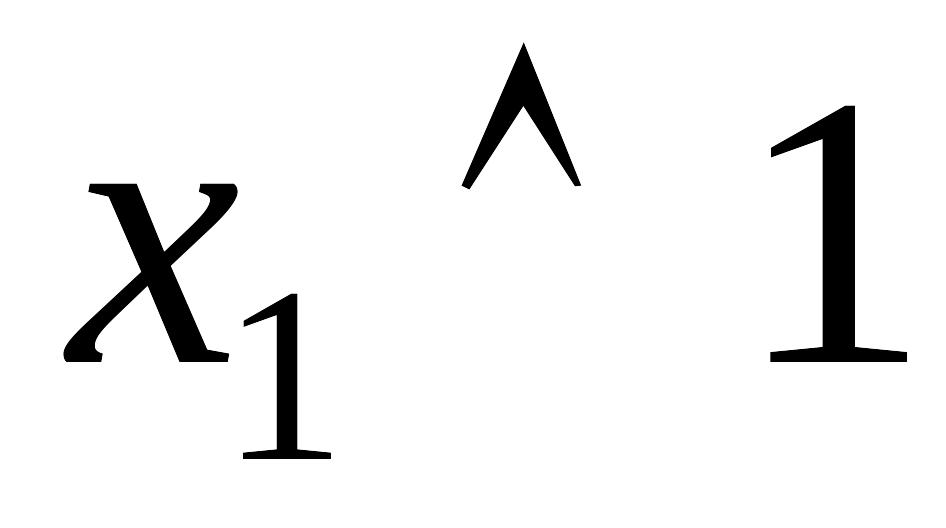
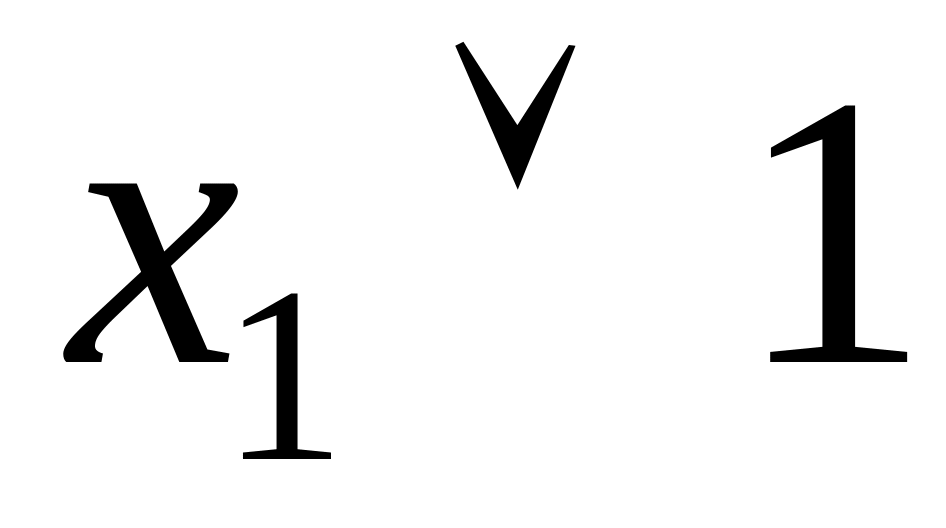
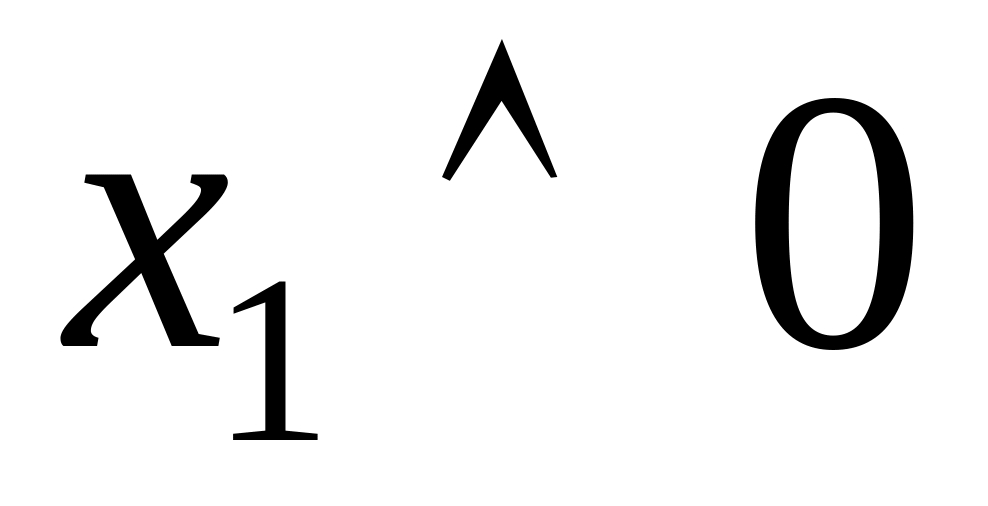
0
0
0
1
0
1
1
1
1
0
Закон поглощения (элиминации)
;
.
Пример.
Докажем закон поглощения (элиминации) аналитически, используя тождества с константами и дистрибутивный закон:
;
.
Закон инволюции (двойного отрицания)
.
Пример.
Для доказательства закона инволюции (двойного отрицания) используем таблицу истинности (таблица 4.14).
Таблица 4.14 Закон двойного отрицания
-
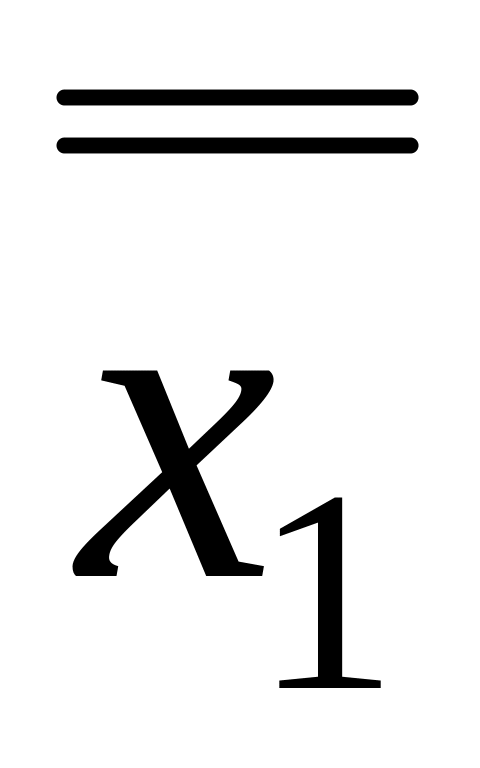
0
1
0
1
0
1
Законы де Моргана
;
.
Пример.
Для доказательства закона де Моргана используем таблицу истинности (таблица 4.15).
Таблица 4.15 Доказательство закона де Моргана
-
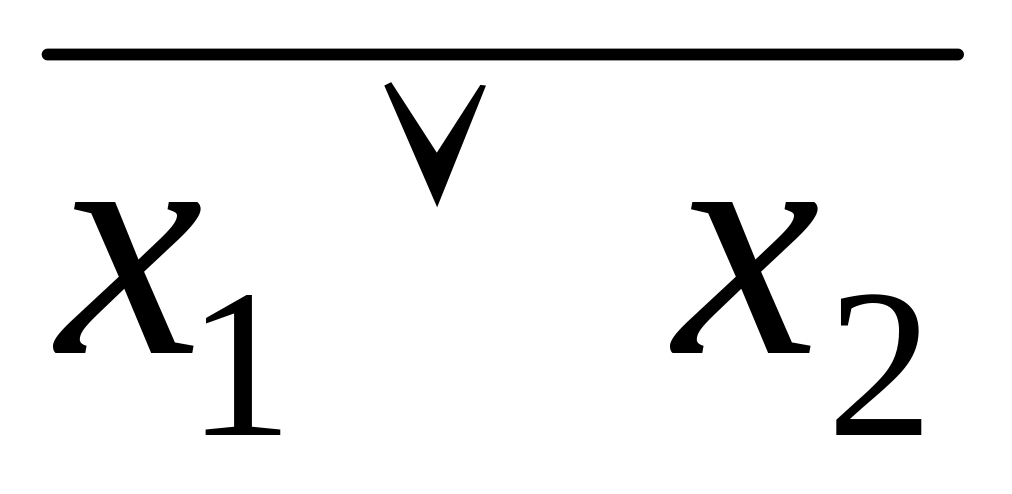
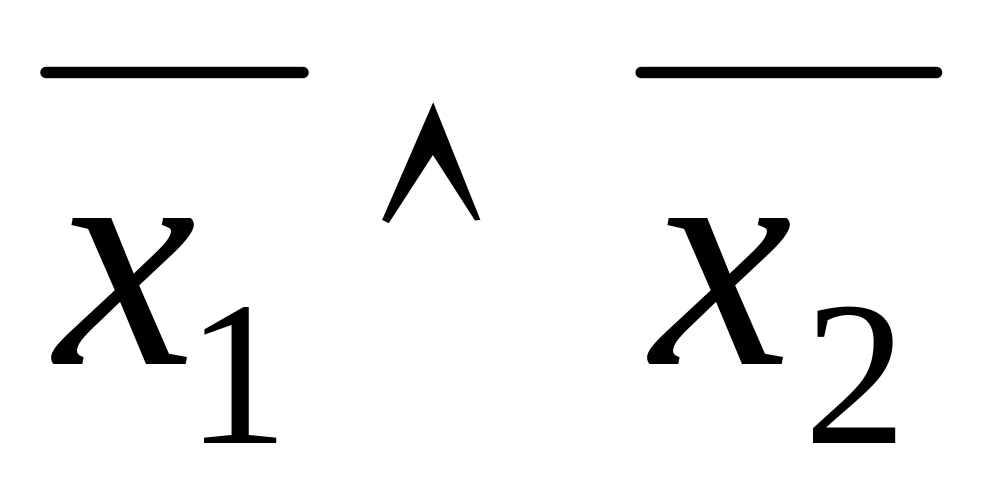
0
0
0
1
1
1
1
0
1
1
0
1
0
0
1
0
1
0
0
1
0
1
1
1
0
0
0
0
Второй закон де Моргана является двойственным первому и, значит, также является верным.
4.3 Контрольные вопросы и задания
4.3.1 Контрольные вопросы
Какие переменные называются булевыми или логическими переменными?
Какая функция называется логической (булевой, переключательной)?
Приведите примеры задания (использования) булевых переменных в языках программирования.
Как называется совокупность конкретных значений аргументов булевой функции?
Сколько элементов-слов содержит -мерный булевый куб?
Что представляет собой область определения и область значений булевой функции?
Какая булева функция называется полностью определенной?
Как определить число всех булевых функций, зависящих от переменных.
Перечислите способы задания булевых функций.
Что представляет собой таблица истинности (соответствия) булевой функции. Назовите правила её построения.
Перечислите булевы функции от одной переменной.
Приведите примеры элементарных функций двух переменных.
Перечислите основные булевы функции от двух переменных.
Каким образом определяется номер булевой функции? Номер интерпретации?
Дайте определение формулы для задания булевой функции. Что такое суперпозиция булевых функций?
Какие знаки используются при образовании (построении) формул? Какой приоритет определен для операций алгебры логики?
Какая запись формул называется инфиксной? Приведите примеры.
Чем отличается табличный и формульный способ задания булевых функций? В каких случаях применяется каждый из них?
Какие формулы называются равносильными или эквивалентными?
Перечислите основные методы определения равносильности формул.
Дайте определение двойственной функции.
Дайте определение самодвойственной функции.
Каким образом формируется таблица истинности двойственной функции?
Сформулируйте принцип двойственности булевых функций.
Дайте определения двухэлементной булевой алгебры и алгебры логики.
Перечислите основные законы булевой алгебры.
Каким способом можно доказать законы булевой алгебры.
Сформулируйте и запишите тождества для законов булевой алгебры.
4.3.2 Контрольные задания
Задание 1.
Во сколько раз больше различных двоичных
слов надо анализировать для булевой
функции
,
чем для булевой функции
?
Задание 2. Во сколько раз больше можно построить булевых функций, зависящих от 6-и переменных, чем от 4-х переменных?
Задание 3. Построить таблицы истинности следующих функций и определить их порядковый номер:
а)
;
б)
;
в)
;
г)
;
д)
.
Задание 4. Проверить с помощью таблиц истинности, справедливы ли следующие соотношения:
а)
;
б)
;
в)
;
г)
;
д)
.
Задание 5.
При
;
;
;
найдите значения функций
и
.
Задание 6.
Доказать, что импликация и эквиваленция
выражаются через другие функции:
;
.
Задание 7.
Используя основные эквивалентности,
доказать эквивалентность формул
и
,
если
,
.
Задание 8. Найти двойственные формулы к следующим функциям:
а)
;
б)
;
в)
.
Задание 9.
Определить, являются ли следующие функции самодвойственными:
а)
;
б)
;
в)
.
Задание 10.
Упростить с помощью законов булевой логики приведенные ниже выражения. Затем с помощью таблиц истинности сравнить полученные выражения с исходными:
а)
;
б)
;
в)
.
Задание 11.
Булева функция
определяется следующим образом: она
равна 1 при
,
либо, если
и
принимают разные значения, а значение
переменной
меньше значения переменной
.
В противном случае функция обращается
в 0. Составить таблицу функции
и записать множество
.