
Лабораторная работа 1
Временные ряды и их предварительный анализ
Проверка гипотезы об отсутствии тенденции
Критерий серий, основанный на медиане выборки
1 Из исходного временного ряда кредиторской задолженности ( ), образуем ранжированный ряд ( ) (таблица 1.1).
Таблица 1.1 – Формирование серий
T |
Кредиторская задолженность |
Ранжированный ряд, у"t |
|
Номер серии |
Протяженность серии |
|
млрд.руб. |
||||
2009 1 |
13201,3 |
13201,3 |
- |
1 |
14 |
2 |
13471,3 |
13471,3 |
- |
||
3 |
13687,8 |
13687,8 |
- |
||
4 |
13734,5 |
13734,5 |
- |
||
5 |
14069,9 |
14069,9 |
- |
||
6 |
14646,5 |
14507,2 |
- |
||
7 |
14507,2 |
14584,9 |
- |
||
8 |
14584,9 |
14646,5 |
- |
||
9 |
15039 |
14656 |
- |
||
10 |
14774,3 |
14774,3 |
- |
||
11 |
14860,6 |
14860,6 |
- |
||
12 |
14881,5 |
14881,5 |
- |
||
2010 1 |
14656 |
14973,2 |
- |
||
2 |
14973,2 |
15039 |
- |
||
3 |
15446,9 |
15251,8 |
+ |
2 |
1 |
4 |
15251,8 |
15446,9 |
- |
3 |
1 |
5 |
15641,7 |
15641,7 |
+ |
4 |
14 |
6 |
16619,5 |
16510,3 |
+ |
||
7 |
16510,3 |
16619,5 |
+ |
||
8 |
16701,2 |
16701,2 |
+ |
||
9 |
17066,9 |
17066,9 |
+ |
||
10 |
17328,6 |
17328,6 |
+ |
||
11 |
17533,3 |
17392,4 |
+ |
||
12 |
17683,4 |
17533,3 |
+ |
||
2011 1 |
17392,4 |
17683,4 |
+ |
||
2 |
18134,7 |
18134,7 |
+ |
||
3 |
18719,1 |
18719,1 |
+ |
||
4 |
18789,1 |
18789,1 |
+ |
||
5 |
19115,4 |
19115,4 |
+ |
||
6 |
19883,4 |
19883,4 |
+ |
2
Определяем медиану (Ме) ранжированного
временного ряда. Так как значение длины
ряда четное, то
![]() ;
;
3
Образуем последовательность
![]() из плюсов и минусов по правилу:
из плюсов и минусов по правилу:
![]()
Если значение уровня исходного ряда yt равно медиане, то это значение пропускается (столбец 4 таблицы 1.1).
4
Подсчитывается
![]() -
число серий в совокупности
-
число серий в совокупности
![]() ,
где под серией понимается последовательность
подряд идущих плюсов и минусов. Один
плюс или один минус тоже будут считаться
серией. Определяется
,
где под серией понимается последовательность
подряд идущих плюсов и минусов. Один
плюс или один минус тоже будут считаться
серией. Определяется
![]() -
протяженность самой длиной серии.
-
протяженность самой длиной серии.
Получаем: =3, =14
5 Чтобы не была отвергнута гипотеза о случайности исходного ряда, должны выполняться следующие неравенства:
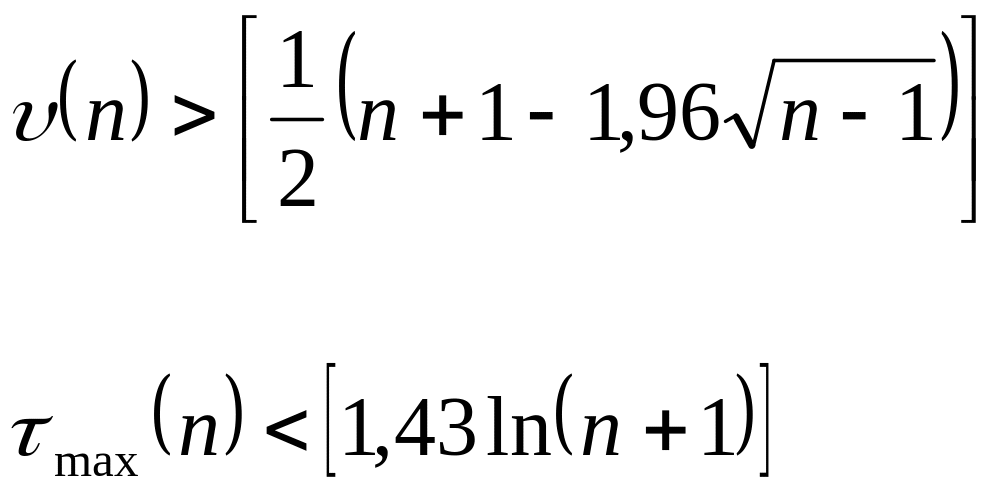 ,
,
где
![]() - длина временного ряда.
- длина временного ряда.
Рассчитаем правые части неравенств:
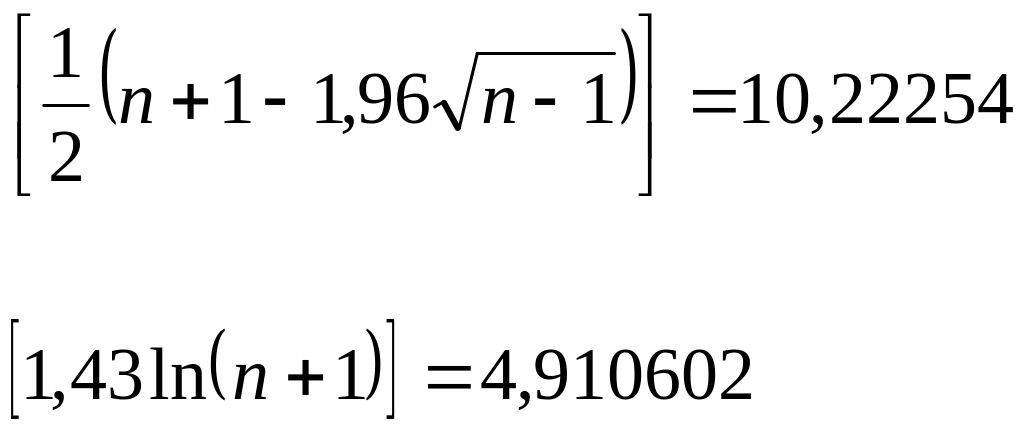
Так как в правой части неравенства стоят квадратные скобки, означающие целую часть числа, то сравнения будем проводить с целыми числами – соответственно с 10 и 4.
Получим:
3 > 10
14 < 4
Оба
неравенства нарушаются, следовательно,
гипотеза отвергается с вероятностью
ошибки
![]() ,
заключенной между 0,05 и 0,0975 (следовательно,
подтверждается наличие зависящей от
времени неслучайной составляющей).
,
заключенной между 0,05 и 0,0975 (следовательно,
подтверждается наличие зависящей от
времени неслучайной составляющей).
