2 Случай. Меньше остальных когда . Тогда ведущей будет третья строка.
Таблица 8
Базисные переменные |
Свободные члены |
|
|
|
|
|
|
|
|
1 |
0,17 |
0,17 |
0 |
0 |
у |
|
1270 – |
0 |
3,83 |
-2,17 |
1 |
0 |
331,3-0,57у |
|
1280 – |
0 |
6,83 |
-1,17 |
0 |
1 |
187,3-0,17у |
Z |
|
0 |
- 1,67 |
2,33 |
0 |
0 |
|
Пересчитывая, получаем новую симплекс таблицу.
Таблица 9
Базисные переменные |
Свободные члены |
|
|
|
|
|
|
-31,2+0,20у |
1 |
0 |
0,20 |
0 |
-0,02 |
|
552+0,51у |
0 |
0 |
-1,52 |
1 |
-0,56 |
|
187,3-0,17у |
0 |
1 |
-0,17 |
0 |
0,15 |
Z |
312,2+2,05у |
0 |
0 |
2,05 |
0 |
0,24 |
Так
как в индексной строке все элементы
неотрицательны, то полученный план
является оптимальным. При
оптимален план
,
,
,
,
,
а значение целевой функции равно
.
3 Случай. Меньше остальных когда . Тогда ведущей будет вторая строка.
Таблица 10
Базисные переменные |
Свободные члены |
|
|
|
|
|
|
|
|
1 |
0,17 |
0,17 |
0 |
0 |
у |
|
1270 – |
0 |
3,83 |
-2,17 |
1 |
0 |
3 31,3-0,57у |
|
1280 – |
0 |
6,83 |
-1,17 |
0 |
1 |
187,3-0,17у |
Z |
|
0 |
- 1,67 |
2,33 |
0 |
0 |
|
Пересчитывая, получаем новую симплекс таблицу.
Таблица 11
Базисные переменные |
Свободные члены |
|
|
|
|
|
|
-55,2+0,26у |
1 |
0 |
0,26 |
-0,04 |
0 |
|
331,3-0,57у |
0 |
1 |
-0,57 |
0,26 |
0 |
|
-983,9+2,70у |
0 |
0 |
2,70 |
-1,78 |
1 |
Z |
552,2+1,39у |
0 |
0 |
1,39 |
0,43 |
0 |
Так
как в индексной строке все элементы
неотрицательны, то полученный план
является оптимальным. При
оптимален план
,
,
,
,
а значение целевой функции равно
.
Объединяя эти случаи, решение можно записать в виде:
Представим эти результаты на графиках с использованием офисной программы MS Excel (рисунок 1, 2).
Таблица 12
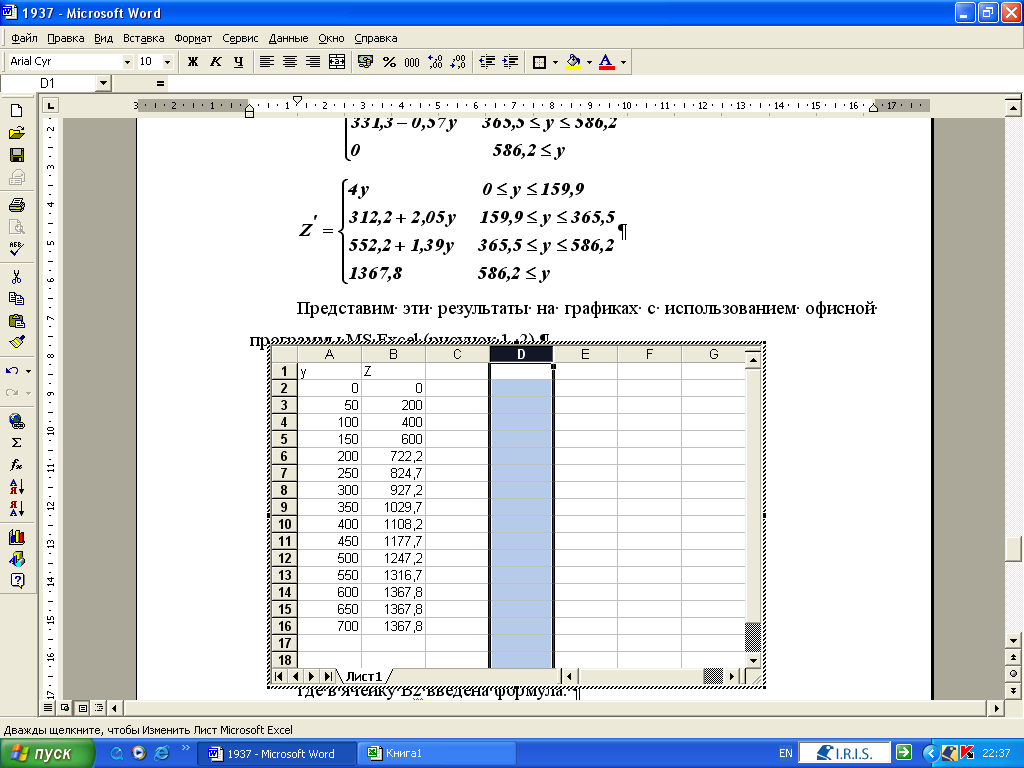
где в ячейку В2 введена формула:
=ЕСЛИ(A2<160;4*A2;ЕСЛИ(A2<365;312,2+2,05*A2;ЕСЛИ(A2<586,2;552,2+1,39*A2;1367,8))) и скопирована на остальные ячейки во втором столбце.
Рисунок 1
Таблица 10
У |
x1 |
x2 |
0 |
0 |
0 |
100 |
0 |
100 |
200 |
8,8 |
153,3 |
300 |
28,8 |
136,3 |
400 |
48,8 |
103,3 |
500 |
74,8 |
46,3 |
600 |
97,7 |
0 |
700 |
97,7 |
0 |
800 |
97,7 |
0 |
Рисунок 2
ЭТАП 2.
Задачу нелинейного программирования предварительно решим графически с помощью программы MS Excel.
Таблица 11
У |
Р |
f |
Z |
F=Z-f |
0 |
8,7 |
0 |
0 |
0 |
50 |
8,7075 |
54,35375 |
200 |
145,6463 |
100 |
7,83 |
107,83 |
400 |
292,17 |
150 |
7,3675 |
161,0513 |
600 |
438,9488 |
200 |
7,32 |
214,64 |
722,2 |
507,56 |
250 |
7,6875 |
269,2188 |
824,7 |
555,4813 |
300 |
8,47 |
325,41 |
927,2 |
601,79 |
350 |
9,6675 |
383,8363 |
1029,7 |
645,8638 |
400 |
11,28 |
445,12 |
1108,2 |
663,08 |
450 |
13,3075 |
509,8838 |
1177,7 |
667,8163 |
500 |
15,75 |
578,75 |
1247,2 |
668,45 |
550 |
18,6075 |
652,3413 |
1316,7 |
664,3588 |
600 |
21,88 |
731,28 |
1367,8 |
636,52 |
650 |
25,5675 |
816,1888 |
1367,8 |
551,6113 |
700 |
29,67 |
907,69 |
1367,8 |
460,11 |
750 |
34,1875 |
1006,406 |
1367,8 |
361,3938 |
800 |
39,12 |
1112,96 |
1367,8 |
254,84 |
Рисунок 3
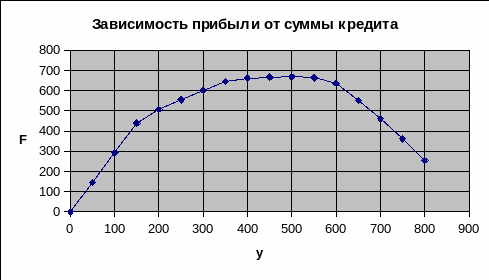
Как
видно из графика и по таблице, оптимальное
значение прибыли достигается при сумме
кредита, лежащей между 400 и 550 млн. руб.
Для получения точного значения, проведем
аналитическое исследование прибыли на
этом интервале. Сумма оптимального
дохода на интервале
,
в который попадает и наш исследуемый
интервал, задается формулой
.
Тогда прибыль равна
.
Раскрывая скобки получаем:
.
Исследуем эту функцию на максимум на интервале .
Приравнивая
первую производную к нулю, найдем
стационарные точки функции:
;
.
Второй корень лежит вне исследуемого
промежутка, и его рассматривать не
будем.
Вычислим вторую производную и определим ее знак в стационарной точке.
.
Следовательно, точка
является точкой максимума. Таким образом,
оптимальная сумма кредита равна 484,5
млн. руб.
Определим
оптимальный план строительства:
,
,
.
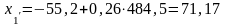ВЫВОД: Для оптимизации прибыли строительной фирме нужно взять кредит в размере 484,5 млн. рублей и построить 71,17 тыс. кв. метров торговых площадей и 57,46 тыс. кв. метров жилых площадей. При этом фирма получит прибыль около 669,74 млн. рублей.