
- •Определение оптимального плана постройки зданий при имеющихся ресурсах и возможностях
- •1. Рассмотрим случай . Тогда и ведущей строкой будет вторая строка:
- •2. Рассмотрим случай когда . Тогда в таблице 1 ведущей строкой будет первая строка.
- •2 Случай. Меньше остальных когда . Тогда ведущей будет третья строка.
- •3 Случай. Меньше остальных когда . Тогда ведущей будет вторая строка.
Определение оптимального плана постройки зданий при имеющихся ресурсах и возможностях
Вариант №23
Дополнительная возможность 1. Получение ссуды. |
|||||||||||||
DT |
RT |
VT |
DЖ |
RЖ |
VЖ |
BD |
BR |
BV |
ST |
SЖ |
P0 |
P1 |
P2 |
6 |
13 |
7 |
1 |
6 |
8 |
0 |
1270 |
1280 |
14 |
4 |
10 |
0,03 |
110 |
Строительная
фирма имеет возможность постройки двух
видов зданий: торговый комплекс или
жилой дом. Каждый вид сооружается в
течение года. Для сооружения тысячи
«торговых» квадратных метров требуется
вложить 6 миллионов рублей, задействовать
13 рабочих и затратить 7 тысяч кубометров
стройматериалов. Для сооружения тысячи
квадратных метров «жилой» площади
требуется вложить 1 миллион рублей,
задействовать 6 рабочих и затратить 8
тысяч кубометров стройматериалов. За
каждую тысячу квадратных метров торговых
площадей фирма получает доход 14 млн.
рублей, а за каждую тысячу кв. жилой
площади – 4 млн. рублей. На складах фирмы
имеется 1280 тысяч кубометров стройматериалов,
в штате фирмы 1270 рабочих, а собственный
капитал фирмы составляет 0
рублей.
Кроме того, фирма может взять кредит в
банке в размере у
млн.
руб., при этом в конце года фирма платит
за кредит
 процентов годовых, если сумма кредита
превышает 50 млн. руб. и
процентов годовых, если сумма кредита
превышает 50 млн. руб. и
 процентов годовых, если сумма кредита
меньше.
процентов годовых, если сумма кредита
меньше.
Определить оптимальный план постройки зданий при имеющихся ресурсах и возможностях. Стоимость своих стройматериалов и штатных рабочих уже включена в баланс и дополнительного учета не требует.
РЕШЕНИЕ.
Составим
экономико-математическую модель задачи.
Для этого обозначим
 - количество тысяч квадратных метров
торговых площадей, а
- количество тысяч квадратных метров
торговых площадей, а
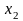 количество
тысяч квадратных метров жилой площади
построенных фирмой. Кредит
количество
тысяч квадратных метров жилой площади
построенных фирмой. Кредит
 (в
млн. руб.), полученный фирмой в банке
может быть любым неотрицательным числом.
(в
млн. руб.), полученный фирмой в банке
может быть любым неотрицательным числом.
Эта задача является задачей оптимального использования ресурсов. Система ограничений, получаемая из ограниченности ресурсов не отрицательности числа квадратных метров, имеет вид:

Целевая функция представляет собой общую стоимость произведенной продукции, и эта функция в поставленных ограничениях оптимизируется на максимум:

где функция
 отражает выплаты банку. Она связана с
процентной ставкой Р
и суммой кредита у
следующим соотношением:
отражает выплаты банку. Она связана с
процентной ставкой Р
и суммой кредита у
следующим соотношением:
 .
.
Согласно условию задачи, получаем:
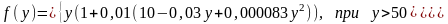
из-за нелинейности функции F к данной задаче нельзя применить методы линейного программирования непосредственно. Задача нелинейного программирования достаточно сложна. Поэтому решение этой задачи разбиваем на 2 этапа.
На первом этапе определяем оптимальный план следующей задачи линейного программирования:

рассматривая у как параметр.
В результате
решения этой задачи получаем оптимальный
план, в котором
 ,
,
 ,
,
 зависят от у.
зависят от у.
На втором этапе
решаем задачу нелинейного программирования.
Ищем
 из задачи
из задачи
 ,
,
которая легко решается графически с последующим уточнением.
ЭТАП 1.
Для решения задачи симплекс методом приведем систему

к каноническому
виду, введя дополнительные балансовые
переменные
 ,
которые означают неиспользованное
количество денег, рабочих и стройматериалов
соответственно:
,
которые означают неиспользованное
количество денег, рабочих и стройматериалов
соответственно:

где все переменные
не отрицательны
 .
.
Целевая функция принимает вид:
 .
.
Составим исходную симплексную таблицу:
Таблица 1
Базисные переменные |
Свободные члены |
|
|
|
|
|
|
|
y |
6 |
1 |
1 |
0 |
0 |
|
|
1270 |
13 |
6 |
0 |
1 |
0 |
97,7 |
|
1 |
7 |
8 |
0 |
0 |
1 |
182,9 |
Z |
0 |
-14 |
-4 |
0 |
0 |
0 |
|
Ведущим столбцом будет первый столбец, так как ему в индексной строке соответствует самое меньшее отрицательное число.
При
определении ведущей строки среди
симплексных отношений нужно выбрать
наименьшее. Очевидно, что
 при
любых значениях у.
Соотношение
между
при
любых значениях у.
Соотношение
между
 и
и
 зависит
от
у.
зависит
от
у.




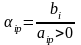
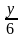
 280
280