Прикладная математика

В любом кольце Z / mZ класс 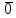никогда не обратим, обратимы лишь те классы 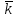, для которых НОД (k, n) = 1. Поэтому их общее количество совпадает с числом φ (n). Вычислим φ(20): 20 = 2² · 5; φ(20) = φ(2²) · φ(5) = 2 · 4 = 8. Из таблицы умножения видим, что обратимыми являются также 8 классов вычетов:

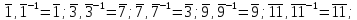
Классы 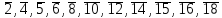не являются обратимыми.

Имеем 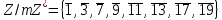. Проверим на цикличность:

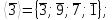
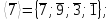
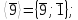
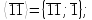
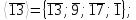
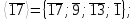
Так как все элементы группы Z / mZ^* не принадлежат ни одной из циклических групп, то группа Z / mZ^* не является циклической.

Задание 4.

Установить истинное сообщение, зашифрованное классическим методом:

а) расшифровать криптограмму Цезаря:

ЪЦХЯ ЕЗЪЗУРЗБ УСФСБ СФЮТГЗХФВ ХУГЕГ;

б) перевести с тарабарского:

КМУЦПО ИФЩЕХАКЬ ЩУЦУБЕЧО. О. УАЙСЬЦ;

в) расшифруйте текст, зашифрованный с помощью девиза «Роза»:

арфбьюхгаыцйгвднбкфэубыбчвкесыс;

г) Прочитайте текст, зашифрованный методом постолбцовой транспозиции (n=5,m=6):

нзььс нтняа ораае ждчгс еюаао кплюн.

Решение задания 4.

а) Используем ключ:

А

Б

В

Г

Д

Е

Ё

Ж

З

И

Й

К

Л

М

Н

О

П

Р

С

Т

У

Ф

Х

Ц

Ч

Ш

Щ

Ъ

Ы

Ь

Э

Ю

Я

Г

Д

Е

Ё

Ж

З

И

Й

К

Л

М

Н

О

П

Р

С

Т

У

Ф

Х

Ц

Ч

Ш

Щ

Ъ

Ы

Ь

Э

Ю

Я

А

Б

В

ЪЦХЯ ЕЗЪЗУРЗБ УСФСБ СФЮТГЗХФВ ХУГЕГ;

ЧУТЬ ВЕЧЕРНЕЮ РОСОЮ ОСЫПАЕТСЯ ТРАВА.

б) Используем ключ:

Б	В	Г	Д	Ж	З	К	Л	М	Н
Щ	Ш	Ч	Ц	Х	Ф	Т	С	Р	П

КМУЦПО ИФЩЕХАКЬ ЩУЦУБЕЧО. О. УАЙСЬЦ;

ТРУДНО ИЗБЕЖАТЬ БУДУЩЕГО. О. УАЙЛЬД.

в) Составим таблицу:

1	18	22	2	30	32	23	4	1	29	24	11	4	3	5	15	2	12	22	31	21	2	29	2	25	3	12	6	19	29	19
а	р	ф	б	ь	ю	х	г	а	ы	ц	й	г	в	д	н	б	к	ф	э	у	б	ы	б	ч	в	к	е	с	ы	с
р	о	з	а	р	о	з	а	р	о	з	а	р	о	з	а	р	о	з	а	р	о	з	а	р	о	з	а	р	о	з
18	16	9	1	18	16	9	1	18	16	9	1	18	16	9	1	18	16	9	1	18	16	9	1	18	16	9	1	18	16	9
------------------------------------------------------------------------------------------------------------------------------
16	2	13	1	12	16	14	3	16	13	15	10	19	20	29	14	17	29	13	30	3	19	20	1	7	20	3	5	1	13	10
о	б	л	а	к	о	м	в	о	л	н	и	с	т	ы	м	п	ы	л	ь	в	с	т	а	е	т	в	д	а	л	и

Получаем фразу: Облаком волнистым пыль встает вдали.

г) Составим матрицу 5х6:

н	а	о	с	е	н
з	я	р	г	ю	ю
ь	н	а	ч	а	л
ь	т	а	д	а	п
с	н	е	ж	о	к

Получим фразу: На осеннюю грязь начал падать снежок.

Задание 5.

Расшифровать криптосообщение RSA.

{m, e, n} = {1378, 11, 1763}.

Решение задания 5.

Для расшифровки необходимо:

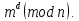
Величина d является обратным к классу вычетов 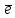в кольце Z / φ(n)Z и находится стандартным расширенным алгоритмом Евклида.

Сначала необходимо разложить число n на простые множители для того, чтобы определить φ(n). Для этого используем метод “решето Эратосфена”: 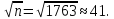Непосредственная подстановка дает n = p · q = 41· 43.

Тогда

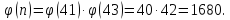
Теперь найдем :

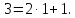
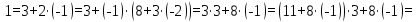
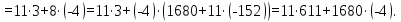
Имеем

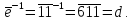
Теперь найдем истинное сообщение:

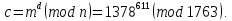
Для этого воспользуемся китайской теоремой об остатках. Найдем CRT-представление 1378 ↔ (25, 2). Оно получается путем вычислений:

1378 = 33·41 + 25; 1378 = 32·43 + 2.

Вычислим:

;

25²(mod 41) = 625 ≡ 10(mod 41);

25⁴(mod 41) = 10² = 100 ≡ 18(mod 41);

25¹¹(mod 41) = 25⁴·25⁴·25²·25(mod 41) ≡ 18·18·10·25(mod 41) ≡ 25(mod 41).

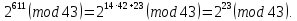
2³(mod 43) = 8(mod 43);

2¹⁰(mod 43) =1024≡ 35(mod 43);

2²³(mod 43) = 2¹⁰·2¹⁰·2³(mod 41) ≡ 35·35·8(mod 41) ≡ 39(mod 41).

Само сообщение с ↔ (25, 39) восстановим с помощью формулы Гарнера. Для ее применения найдем 41^-1(mod 43) с помощью расширенного алгоритма Евклида:

43 = 41·1+2; 41 = 2·20+1.

.

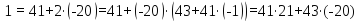Следовательно 41^-1(mod 43) = 21.

Тогда истинное сообщение с:

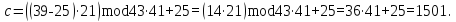
Истинное сообщение соответствует буквосочетанию «НА».

Задание 6.

Расшифровать криптосообщение Эль Гамаля.

{m, O, P, g, h, x}={44,57,61,10,14,10}.

Решение задания 6.

Вычисляем K = O^x (mod P) = 57¹⁰(mod 61); 57² = 3249 ≡ 16(mod 61);

57⁴ ≡ 16² = 12(mod 61); 57¹⁰ = 57⁴·57⁴·57² ≡ 12·12·16 = 2304 = 47(mod 61). Итак K = 47.

Найдем K^-1 в Z / 61Z с помощью расширенного алгоритма Евклида:

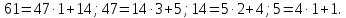Строим Соотношение Безу для НОД(61, 47) = 1.

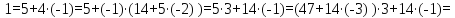
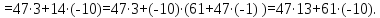
Из полученного соотношения Безу следует, что K^-1 = 13. Тогда 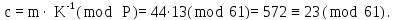Таким образом искомое сообщение равно 23, что совпадает с буквой «Х».

Задание 7.

Расшифровать криптосообщение Рабина.

{N, B, m}= {3713,1000,732}.

Решение задания 7.

Искомое сообщение с есть один из корней квадратного уравнения х² + Вх – т = 0 в кольце Z / NZ. В данном случае с есть один из корней уравнения х² + 1000х – 732 = 0 в кольце Z / NZ. В этом кольце 2, очевидно, является обратимым элементом. Поэтому для решения данного квадратного уравнения вполне пригодны стандартные формулы:

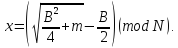Здесь

.

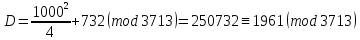Необходимо найти в кольце Z/3713Z квадратные корни из D = 1961. Для этого воспользуемся китайской теоремой об остатках.

Найдем разложение модуля N = 3713 на простые множители p и q. N = 47·79 = 3713, то есть p = 47 и q = 79. Найдем CRT-представление 1961 ↔ (34, 65). Оно получается путем вычислений:

1961 = 41·47 + 34; 1961 = 24·79 + 65.

Найдем квадратные корни из 34 в поле Z/47Z. Убедимся, что 34 является квадратом в поле Z/47Z. Согласно критерию Эйлера целое число z из множества {1, 2, … p-1} является квадратом в Z/pZ тогда и только тогда, когда

Вычислим

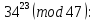
34²(mod 47) = 1156 ≡ 28(mod 47);

34⁴(mod 47) = 28² = 784 ≡ 32(mod 47);

34⁸(mod 47) = 32² = 1024 ≡ 37(mod 47);

34¹⁶(mod 47) = 37² = 1369 ≡ 6(mod 47).

34²³(mod 47) = 34¹⁶ · 34⁴ · 34² · 34(mod 47) ≡ 6·32·28·34(mod 47) =1.

Таким образом, 34 действительно является квадратом в поле из 47 элементов.

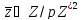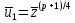Известно, что в поле Z/pZ с условием p = 3(mod 4), из всякого квадрата извлекаются два различных квадратных корня: и

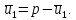
В нашем случае u₁= 34¹²(mod 47) ≡ 37·32 = 1184 = 9(mod 47); u₂ = 47 – 9=38.

Найдем квадратные корни из 65 в поле Z/79Z. Убедимся, что 65 является квадратом в поле Z/79Z.

Вычислим 65³⁹(mod 79):

65²(mod 79) = 4225 ≡ 38(mod 79);

65⁴(mod 79) = 38² = 1444 ≡ 22(mod 79);

65⁸(mod 79) = 22² = 484 ≡ 10(mod 79);

65¹⁶(mod 79) = 10² = 100 ≡ 21(mod 79);

65³²(mod 79) = 21² = 441 ≡ 46(mod 79).

65²³(mod 79) = 65³² · 65⁴ · 65² · 65(mod 79) ≡ 46·22·38·65(mod 79) =1.

Таким образом, 65 действительно является квадратом в поле из 79 элементов.

Найдем квадратные корн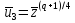и: и

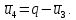
В нашем случае u₃ = 65²⁰(mod 79) = 65¹⁶⁺⁴(mod 79) ≡ 21·22(mod 79) = 462 = = 67(mod 79); u₄=79 – 67 =12.

Получим CRT-представление четырех корней из D = 1961 в кольце Z/3713Z:

d₁ ↔ (9, 67); d₂ ↔ (9, 12); d₃ ↔ (38, 67); d₄ ↔ (38, 12).

Сами корни восстановим с помощью формулы Гарнера. Для ее применения найдем 47^-1(mod 79) с помощью расширенного алгоритма Евклида:

79 = 47·1 + 32; 47 = 32·1 + 15; 32 = 15·2 + 2; 15 = 2·7 + 1.

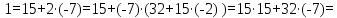
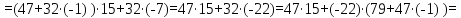
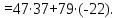
Следовательно, 47^-1(mod 79) = 37.

d₁ = (67 – 9) · 37(mod 79) · 47 + 9 = 620;

d₂ = (12 – 9) · 37(mod 79) · 47 + 9 = 1513;

d₃ = (67 – 38) · 37(mod 79) · 47 + 38 = 2200;

d₄ = (12 – 38) · 37(mod 79) · 47 + 38 = 3093.

Отсюда получим:

x₁ = (620 – 500)(mod 3713) = 120;

x₂ = (1513 – 500)(mod 3713) = 1013;

x₃ = (2200 – 500)(mod 3713) = 1700;

x₄ = (3093 – 500)(mod 3713) = 2593.

Первый корень уравнения соответствует буквосочетанию «АТ», второй - «ИЛ», третий и четвертый не имеют буквенного эквивалента. Из всех ответов наиболее осмысленный - «ИЛ». Его и следует считать правильным ответом.

Задание 8.

Убедиться в неприводимости и примитивности данного полинома p(x) = x⁵ + x⁴ + x² + x +1 с коэффициентами из Z/2Z. Сформировать с помощью этого полинома поле Галуа из 32-х элементов. Выписать проверочную матрицу Н двоичного реверсивного кода длиной 31, исправляющего двойные ошибки.

Решение задания 8.

р(0) = 1≠0; р(1)= 1≠0; p(x) = x⁵ + x⁴ + x² + x +1 = (х²+х+1)·(х³+х)+1–не делится на единственный неприводимый полином второй степени х²+х+1. Поэтому p(x) = x⁵ + x⁴ + x² + x +1 неприводим над полем Z /2Z.

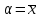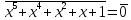В силу неприводимости полинома p(x) = x⁵ + x⁴ + x² + x +1 фактор-кольцо Z/2Z [x]/ < x⁵ + x⁴ + x² + x +1> является полем GF(32) из 32 элементов. Это фактор-кольцо состоит из классов смежности, порождённых всевозможными полиномами из Z/2Z[x], степени которых меньше пятой. При этом смежный класс является корнем полинома p(x) = x⁵ + x⁴ + x² + x +1, поскольку класс смежности . Полином p(x) = x⁵ + x⁴ + x² + x +1 является примитивным, если циклическая группа <α>=GF(32)* состоит из 31 различных степеней α. Это означает, что в таблице степеней α класс 1 должен стоять на последнем 31-м месте, поскольку дальше пойдёт повторение степеней.

Выпишем все элементы циклической группы < α >:

α	α	(00010)
α2	α2	(00100)
α3	α3	(01000)
α4	α4	(10000)
α5	α4 + α2 + α + 1	(10111)
α6	α4 + α3 + 1	(11001)
α7	α2 + 1	(00101)
α8	α3 + α	(01010)
α9	α4 + α2	(10100)
α10	α4 + α3 + α2 + α + 1	(11111)
α11	α3 + 1	(01001)
α12	α4 + α	(10010)
α13	α4 + α + 1	(10011)
α14	α4 + 1	(10001)
α15	α4 + α2 + 1	(10101)
α16	α4 + α3 + α2 + 1	(11101)
α17	α3 + α2 + 1	(01101)
α18	α4 + α3 + α	(11010)
α19	α + 1	(00011)
α20	α2 + α	(00110)
α21	α3 + α2	(01100)
α22	α4 + α3	(11000)
α23	α2 + α + 1	(00111)
α24	α3 + α2 + α	(01110)
α25	α4 + α3 + α2	(11100)
α26	α3 + α2 + α + 1	(01111)
α27	α4 + α3 + α2 + α	(11110)
α28	α3 + α + 1	(01011)
α29	α4 + α2 + α	(10110)
α30	α4 + α3 + α + 1	(11011)
α31	1	(00001)
	0	(00000)

Следовательно, данный полином x⁵ + x⁴ + x² + x +1 является примитивным.

Элементы данной таблицы также будут являться элементами поля Галуа GF (2⁵).

Составим проверочную матрицу Н_R = (αⁱ, α^-1)^T двоичного реверсивного кода длиной 31, исправляющего двойные ошибки, где 0 ≤ i ≤ 2^m – 2, α – корень полинома p(x) = x⁵ + x⁴ + x² + x +1.