
Основы дискретной математики
Функции, отношения и множества. Основы логики, логика
высказываний, логические связки, таблицы истинности. Графы и деревья:
деревья, неориентированные графы, ориентированные графы, стратегии
обхода графов.
Раздел 2 Основы дискретной математики
Тема 1: Основы дискретной математики
План:
Множества, функции, отношения.
Основы логики.
Графы и деревья.
Множества, функции, отношения.
Теория множеств опирается на три первичных понятия:
1) множество;
2) элемент;
3) принадлежность.
Строгого определения этим понятиям не дается, описывается только их применение.
Н а
рисунке 1.1 буквой А
обозначено множество, элементами
которого являются точки заштрихованной
части плоскости, при этом точка а
принадлежит множеству А
(
а
рисунке 1.1 буквой А
обозначено множество, элементами
которого являются точки заштрихованной
части плоскости, при этом точка а
принадлежит множеству А
(![]() ),
точка с не принадлежит множеству А
(
),
точка с не принадлежит множеству А
(![]() ).
).
Способы
задания множеств. Множество
можно задать, перечислив все его
элементы:
![]() ,
,
![]() .
Порядок
записи элементов множества произволен.
Часто задают множество, указав его
характеристическое свойство, которое
для каждого элемента позволяет выяснить,
принадлежит он множеству или нет.
.
Порядок
записи элементов множества произволен.
Часто задают множество, указав его
характеристическое свойство, которое
для каждого элемента позволяет выяснить,
принадлежит он множеству или нет.
Например,
![]() – целый
корень уравнения
– целый
корень уравнения
![]() ,
,
![]() –
целое }.
–
целое }.
В дальнейшем для известных числовых множеств будут использоваться обозначения:
= { 1,2,3,…} – множество натуральных чисел;
Z = { …, -2,-1,0,1,2,…} – множество целых чисел;
Q – множество рациональных чисел;
R – множество действительных чисел.
Основные определения
Пустым
множеством
называется множество ,
не содержащее ни одного элемента, т.е.
для любого элемента x
выполняется
![]() .
.
Универсальным называется множество U всех элементов, рассматриваемых в данной задаче.
Пример.
Пусть U
= Z
и требуется найти все решения уравнения
![]() .
Множество М
решений этой задачи есть пустое множество:
М
= .
.
Множество М
решений этой задачи есть пустое множество:
М
= .
Пусть теперь U
= R.
Тогда множество М
решений уравнения
не пусто: М
=
![]() .
.
Будем говорить,
что множество А
включается
во множество
В
![]() ,
если каждый элемент множества А
является элементом множества В
( говорят также, что А
является подмножеством множества В).
Из определения включения следуют
свойства:
,
если каждый элемент множества А
является элементом множества В
( говорят также, что А
является подмножеством множества В).
Из определения включения следуют
свойства:
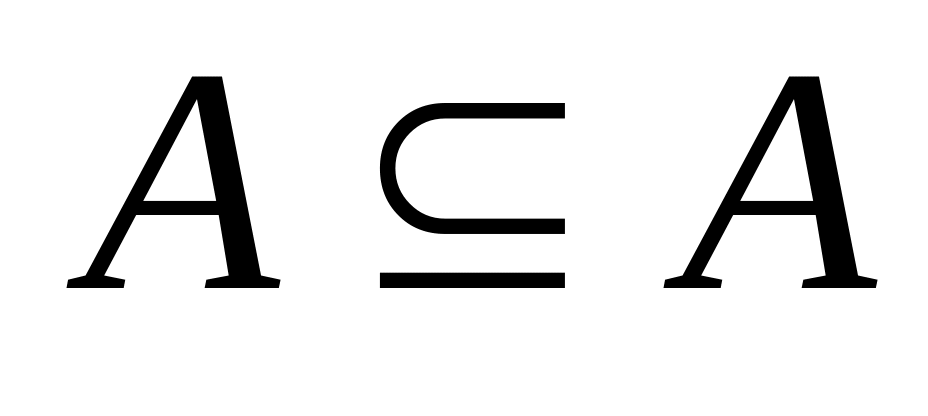 для любого множества
А;
для любого множества
А;Если
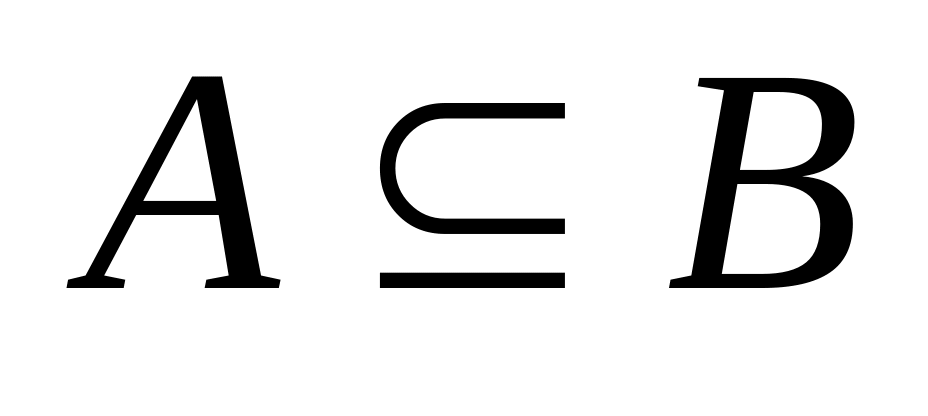 и
и
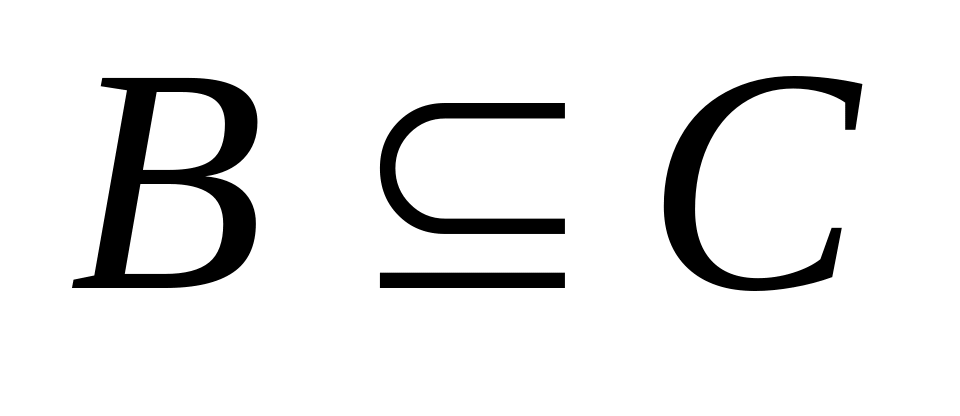 ,
то
,
то
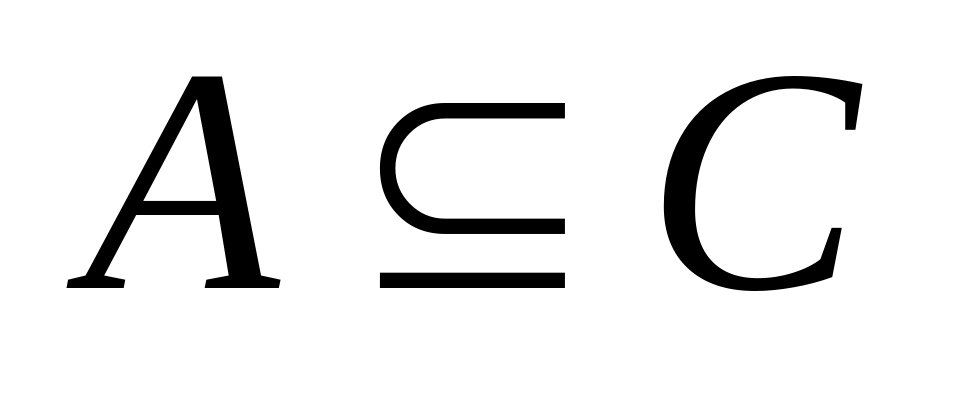 ;
;
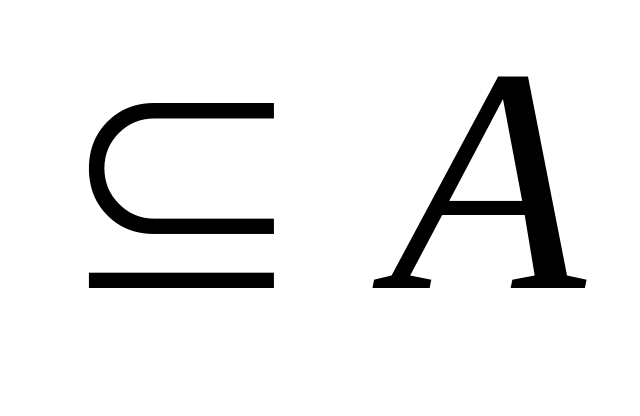 для любого множества
А;
для любого множества
А;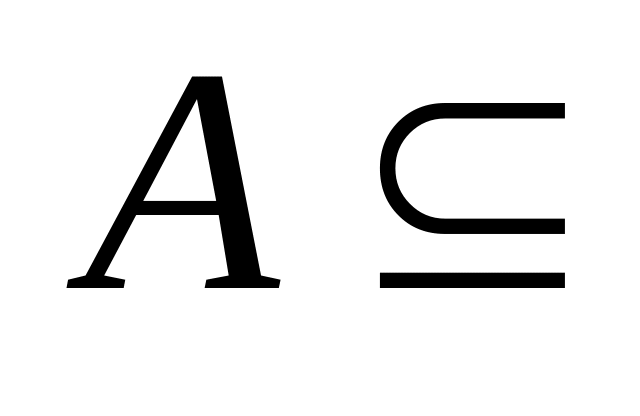 U
для любого множества А.
U
для любого множества А.
Определим понятие
равенства
множеств:
А=В тогда
и только тогда, когда одновременно
выполняются два включения
и
![]() ,
т.е. каждый элемент множества А
является элементом множества В
и каждый элемент множества В
является элементом множества А.
,
т.е. каждый элемент множества А
является элементом множества В
и каждый элемент множества В
является элементом множества А.
Диаграммы Эйлера – Венна. Эти диаграммы применяются для наглядного изображения множеств и их взаимного расположения.
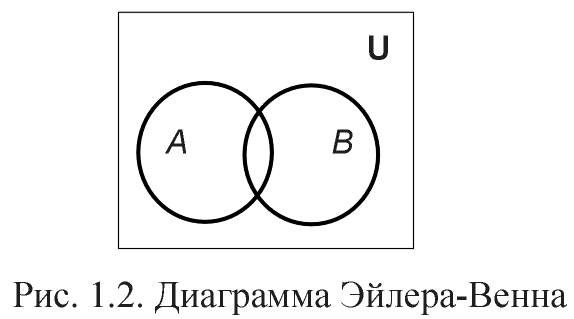
Универсальное множество U изображается в виде прямоугольника, а произвольные множества – подмножества универсального – в виде кругов (рис. 1.2).
Операции над
множествами. Объединением множеств
А и В называется множество
![]() ,
состоящее из тех и только тех элементов,
которые принадлежат хотя бы одному из
множеств А или В (рис.1.3, а).
,
состоящее из тех и только тех элементов,
которые принадлежат хотя бы одному из
множеств А или В (рис.1.3, а).
Пример. Если
![]() ,
то
,
то
![]() .
.
Пересечением
множеств А и В называется
множество
![]() ,
состоящее из тех и только тех элементов,
которые принадлежат одновременно и
множеству А, и множеству В (рис.
1.3, б).
,
состоящее из тех и только тех элементов,
которые принадлежат одновременно и
множеству А, и множеству В (рис.
1.3, б).
П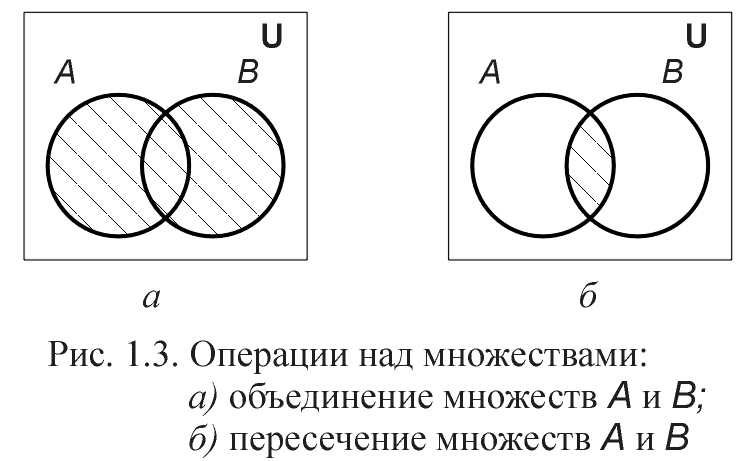 ример.
Если
,
то
ример.
Если
,
то
![]() .
.
Разностью
множеств А и В называется множество
![]() тех и только тех элементов, которые
принадлежат множеству А и не принадлежат
множеству В (рис. 1.4, а).
тех и только тех элементов, которые
принадлежат множеству А и не принадлежат
множеству В (рис. 1.4, а).
Пример.
![]() ;
;
![]() .
.
Дополнением
множества А до универсального U
называется множество
![]() U
U![]() (рис. 1.4, б).
(рис. 1.4, б).
П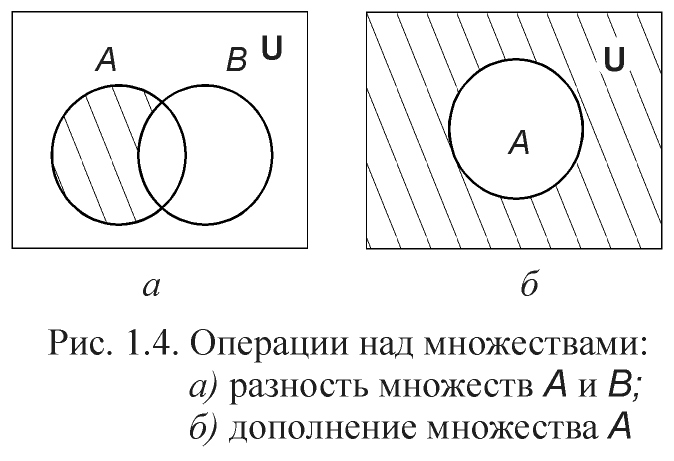 ример.
Если
ример.
Если
![]() ,
U
,
U![]() ,
то
U
,
то
U![]() .
.
Элементы множества
сами могут быть множествами:
![]() ;
в таком случае удобно говорить о системе
множеств. Рассмотрим такие системы
множеств, как булеан и разбиение множеств.
;
в таком случае удобно говорить о системе
множеств. Рассмотрим такие системы
множеств, как булеан и разбиение множеств.
Булеаном B(Х)
множества Х
называется множество всех подмножеств
множества Х.
Например, для множества
![]() булеаном является множество B
булеаном является множество B![]() ,
,![]() .
.
Р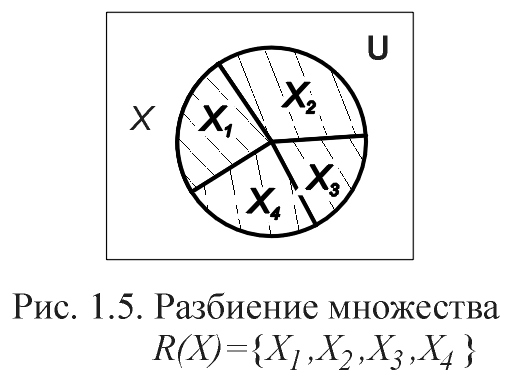 азбиением
R(Х)
множества Х
называется система его непустых
непересекающихся подмножеств, в
объединении дающая множество Х
(рис.1.5).
азбиением
R(Х)
множества Х
называется система его непустых
непересекающихся подмножеств, в
объединении дающая множество Х
(рис.1.5).
Например, для
множества
![]() можно построить разбиение R1
можно построить разбиение R1![]() ,
состоящее из двух элементов (они
называются блоками разбиения), или
разбиение R2
,
состоящее из двух элементов (они
называются блоками разбиения), или
разбиение R2![]() – из четырех блоков; возможны и другие
разбиения этого множества Х.
– из четырех блоков; возможны и другие
разбиения этого множества Х.
Основы логики
Основоположником математической логики является английский математик Джордж Буль (1815 – 1864). Он впервые высказал идеи логического истолкования теории множеств.
Рассмотрим 2х элементное множество B, элементы которого 0 и 1. Однако они не являются числами в обычном смысле. Наиболее распространенная интерпретация двоичных переменных – это логические: “ДА – НЕТ” или “ИСТИННО – ЛОЖНО”. Например: в языках программирования вводится специальный тип переменной – логическая переменная, значения которой обозначаются TRUE и FALSE.
Таким образом, элементы множества B={0,1} будем рассматривать как формальные символы, а не числа.
Алгебра, образованная множеством B вместе со всеми возможными операциями на нем, называется алгеброй логики или Булевой алгеброй.
Булевой функцией f(x1, x2, … , xn) называется функция, которая принимает два значения 0 или 1 в зависимости от переменных хi , каждая из которых может также принимать только два значения 0 или 1.
В таблице наборы переменных расположены в определенном порядке, который совпадает с порядком возрастания наборов, рассматриваемых как двоичные числа. Этим упорядочиванием будем пользоваться и дальше.
Рассмотрим основные функции алгебры логики.
Логическое отрицание (инверсия) обозначается чертой над аргументом. Это функция одной переменной:
f (x)
= x;
0 =1; 1=0.
(x)
= x;
0 =1; 1=0.
2. Логическое сложение (дизъюнкция). Это функция нескольких переменных. Функция обозначается следующим образом:
f(x1,x2) = x1 V x2 V x3…
Для двух переменных таблица истинности имеет вид:
x1 x2 f(x1,x2)
0 0 0
0 1 1
1 0 1
1 1 1
3. Логическое умножение (конъюнкция). Это функция нескольких переменных. Функция обозначается следующим образом:
f(x1x2) = x1 /\ x2 /\ х3 …
Функция определяется следующей таблицей истинности для двух переменных.
x1 x2 f(x1x2)
0 0 0
0 1 0
1 0 0
1 1 1
4. Функция Шеффера – реализует умножение с отрицанием. Определяется для двух переменных следующей таблицей истинности. Это функция нескольких переменных:
x1 x2 f(x1x2)
0 0 1
0 1 1
1 0 1
1 1 0
Функция имеет вид:

f(x1x2) = x1x2 = x1 /\ x2
5. Функция Пирса реализует логическое сложение с отрицанием. Определяется следующей таблицей истинности для двух переменных
x1 x2 f(x1x2)
0 0 1
0 1 0
1 0 0
 1 1 0
1 1 0
Функция имеет вид: f(x1x2) = x1 x2 = x1 x2
Функции дизъюнкции и конъюнкции могут быть не только функциями двух переменных. В общем случае произвольного числа аргументов.
6. Сложение по mod 2. Выполняет логическую операцию XOR. Это функция нескольких переменных и определяется следующей таблицей истинности для двух переменных:
x1 |
x2 |
Y |
0 0 1 1 |
0 1 0 1 |
0 1 1 0 |
Функция имеет вид Y =x1 x2
Всякая логическая функция “n” переменных может быть задана таблицей, в левой части которой перечислены все 2n наборов значений переменных, а в правой части – значения функции на этих наборах. Например, для 3-х переменных имеем:
x1 |
x2 |
x3 |
f |
0 0 0 0 1 1 1 1 |
0 0 1 1 0 0 1 1 |
0 1 0 1 0 1 0 1 |
0 1 0 0 1 1 0 0 |
Наборы (строки) х на которых функция f=1 называют единичным набором, а множество единичных наборов – единичным множеством f.
Наборы х на которых f=0, называют нулевым набором f.
Составим логическую функцию из таблицы значений. Для этого возьмем конъюнкции аргументов в той строке, где функция равна единице. Причем, если аргумент равен нулю – он берется с инверсией. Если аргумент равен единице – он берется с без инверсии. Полученные конъюнкции соединяем дизъюнкцией. Для нашего примера имеем три конъюнкции (три строки таблицы, где функция равна единице). Логическая функция имеет вид:

f = (X1 /\ X2 /\ X3) \/ (X1 /\ X2 /\ X3) \/ (X1 /\ X2 /\ X3)
Инверсия обозначается чертой над аргументом. В первой конъюнкции аргументы Х1, Х2 взяты с инверсией, так как их значения во второй строке таблицы равны нулю. Во второй конъюнкции аргументы Х2, Х3 взяты с инверсией, так как их значения в пятой строке таблицы равны нулю. В третьей конъюнкции аргумент Х2 взят с инверсией, так как его значение в шестой строке таблицы равно нулю. Полученные конъюнкции объединены операциями дизъюнкции.
