Решение задачи № 5 в

Обозначим для краткости и удобства предел пункта в) через

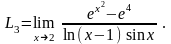
Вычислим пределы трёх функций

, и ,

из которых составлено выражение, стоящее под знаком предела.

Отсюда видим, что функции и являются бесконечно малыми функциями в точке , и что перед нами задача о раскрытии неопределённости вида .

Представим выражение, стоящее под знаком предела в виде произведения двух дробей

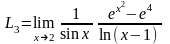
и проведём рассуждения, типичные при вычислении пределов такого сорта.

Предел первой дроби существует и конечен. Предположим, что предел второй дроби тоже существует и конечен. Тогда можно воспользоваться теоремой о пределе произведения двух функций, утверждающей, что предел произведения двух функций, имеющих конечный предел, существует и равен произведению пределов сомножителей.

Чтобы раскрыть неопределённость вида в последнем пределе, заменим бесконечно малые функции и в точке на эквивалентные. Преобразуем эти функции таким образом, чтобы можно было воспользоваться соотношениями эквивалентности:

и при .

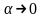В результате получим, что

1. , где роль бесконечно малой функции играет при ;

2. , где роль бесконечно малой функции играет при .

Эта замена позволяет нам раскрыть неопределённость и вычислить предел

Ответ: .

Решение задачи № 5 г

Обозначим для краткости и удобства предел пункта г) через

Пределы функций, стоящих в числителе и знаменателе, равны нулю при , и мы вновь имеем задачу о раскрытии неопределённости вида .

1. Преобразуем функцию так, чтобы можно было воспользоваться соотношениями эквивалентности:

при .

В результате получаем

при ,

где роль бесконечно малой функции играет при .

2. Преобразуем выражение 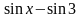с помощью тригонометрической формулы

так, чтобы можно было воспользоваться соотношением эквивалентности: 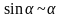при .

В результате получаем

при ,

где роль бесконечно малой функции играет при .

После замены бесконечно малых функций, стоящих в числителе и знаменателе, на эквивалентные в исходном пределе № 5 г мы раскрываем неопределённость, и после выполнения простых преобразований получаем

Ответ: .

Контрольная работа № 1 по аналитической геометрии на плоскости

Вариант I

1. Дан треугольник 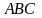с координатами вершин , и . Найти угол между медианой и высотой, проведенными из вершины .

2. Составить каноническое уравнение эллипса и построить кривую, если известны суммы длин его полуосей и эксцентриситет .

3. Найти уравнение прямой, проходящей через левый фокус эллипса , и перпендикулярной прямой, соединяющей центр окружности и фокус параболы .

4. Привести уравнение к каноническому виду. Построить кривую, соответствующую этому уравнению.

Вариант 2

1. Даны две смежные вершины , параллелограмма и точка пересечения его диагоналей. Составить уравнения сторон параллелограмма.

2. Гипербола проходит через точку 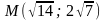и ее эксцентриситет равен . Найти уравнения гиперболы и ее асимптот. Построить гиперболу.

3. Найти уравнение прямой, проходящей через правый фокус эллипса перпендикулярно той асимптоте гиперболы , которая проходит через 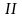и квадранты.

4. Привести уравнение к каноническому виду. Построить кривую, соответствующую этому уравнению.

Вариант 3

1. Даны уравнения двух сторон параллелограмма , и точка пересечения его диагоналей. Составить уравнения двух других сторон параллелограмма.

2. Гипербола проходит через точку и ее асимптоты имеют уравнения . Найти ее уравнение и построить кривую.

3. Найти уравнение прямой, проходящей через левый фокус эллипса и центр окружности .

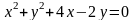4. Привести уравнение к каноническому виду. Построить кривую, соответствующую этому уравнению.

Вариант 4

1. Треугольник задан сторонами , , . Найти уравнение средней линии треугольника , параллельной стороне .

2. Составить уравнение окружности, проходящей через фокус параболы , если ее центр совпадает с правым фокусом эллипса .

3. Найти угол между асимптотой гиперболы , проходящей через и квадранты, и прямой, соединяющей центр окружности 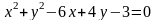и левый фокус эллипса .

4. Привести уравнение к каноническому виду. Построить кривую, соответствующую этому уравнению.

Вариант 5

1. Точк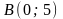и , и образуют вершины треугольника. Найти угол между стороной и медианой .

2. Составить каноническое уравнение гиперболы, если известны уравнения ее асимптот и расстояние между фокусами равно .

3. Найти уравнение прямой, проходящей через фокус параболы параллельно прямой, соединяющей центр окружности с верхней вершиной эллипса .

4. Привести уравнение к каноническому виду. Построить кривую, соответствующую этому уравнению.

Вариант 6

1. Заданы уравнения диагоналей квадрата , и координаты одной из его вершин . Найти уравнения всех сторон квадрата.

2. Парабола проходит через точки пересечения прямой с окружностью , и симметрична относительно оси . Найти каноническое уравнение этой параболы.

3. Найти точку, симметричную с центром окружности 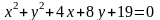относительно прямой, соединяющей левый фокус эллипса 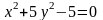с фокусом параболы .

4. Привести уравнение 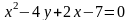к каноническому виду. Построить кривую, соответствующую этому уравнению.

Вариант 7

1. Дан треугольник с координатами вершин , , . Найти уравнение перпендикуляра, опущенного из вершины на медиану, проведенную из вершины .

2. Составить каноническое уравнение гиперболы, вершины которой находятся в фокусах эллипса , а фокусы совпадают с вершинами эллипса.

3. Найти уравнение прямой, проходящей через центр окружности параллельно асимптоте гиперболы , проходящей через и квадранты.

4. Привести уравнение к каноническому виду. Построить кривую, соответствующую этому уравнению.

Вариант 8

1. Найти координаты вершин ромба, если известны уравнения двух его сторон 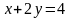, и уравнение одной из его диагоналей .

2. Найти каноническое уравнение гиперболы, если ее асимптоты заданы уравнениями , а один из фокусов находится в точке .

3. Пусть – правый фокус, а –верхняя вершина эллипса 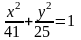. Найти точку на отрезке , которая делит его в отношении , т. е. .

4. Привести уравнение 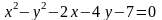к каноническому виду. Построить кривую, соответствующую этому уравнению.

Вариант 9

1. Даны уравнения сторон треугольника , и 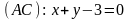. Найти координаты вершин треугольника и тангенсы его внутренних углов.

2. Найти уравнение окружности, имеющей центр в точке и проходящей через фокус параболы .

3. Найти точку симметричную с началом координат относительно прямой, проходящей через точку 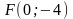параллельно прямой .

4. Привести уравнение к каноническому виду. Построить кривую, соответствующую этому уравнению.

Вариант 10

1. Даны уравнения сторон треугольника ,

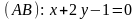и . Составить

уравнение прямой, проходящей через вершину параллельно

противоположной стороне.

2. Найти каноническое уравнение гиперболы, если ее фокус

совпадает с центром окружности , а асимптоты

имеют уравнения .

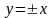3. Найти проекцию фокуса параболы на асимптоту гиперболы , проходящей через и квадранты.

4. Привести уравнение к каноническому виду. Построить кривую, соответствующую этому уравнению.