Решение задачи № 5 а

Обозначим для краткости и удобства предел пункта а) через

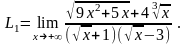
Исследуем, как ведут себя числитель и знаменатель дроби, стоящей под знаком предела, при на «интуитивном уровне». Начнём исследование с числителя. В выражении 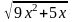можно пренебречь слагаемым , так как оно растёт значительно медленнее, чем . Более точно, говорят, что бесконечно большая величина является бесконечно большой величиной высшего порядка, чем бесконечно большая . Следовательно, . Второе слагаемое числителя и им тоже можно пренебречь по сравнению с первым по тем же соображениям. Таким образом, числитель стремится к как ( в первой степени): при .

Аналогичные рассуждения позволяют установить, что и знаменатель дроби стремится к как в первой степени: при .

Таким образом, перед нами задача о раскрытии неопределённости . Более того, на «интуитивном уровне» мы получаем и значение предела :

Для строго доказательства того, что предел , разделим числитель и знаменатель дроби на (величину, определяющую «скорость стремления числителя и знаменателя на бесконечность»).

Принимая во внимание, что

, ,

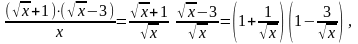
получаем

Данный предел уже не содержит «неопределённости» и для его вычисления применим теорему о пределе частного двух функций.

Учитывая, что при , окончательно получаем, что

Ответ: предел .

Решение задачи № 5 б

Обозначим для краткости и удобства предел пункта б) через

Так как и , то перед нами задача о раскрытии неопределенности вида . Для ее раскрытия воспользуемся формулой , в которой сомножители и будем называть сопряженными друг другу.

Умножим и разделим выражение, стоящее под знаком предела в числителе, на сопряженное ему выражение , в результате получим:

В последнем пределе мы пришли к задаче о раскрытии неопределенности вида . Проведём рассуждения, аналогичные тем, которые были сделаны при вычислении предела № 5 а. Мы видим, что числитель стремится к как ( в первой степени), а знаменатель дроби стремится к как 2 ( во второй степени), т. е. скорость знаменателя является бесконечно большой величиной высшего порядка, чем скорость числителя, поэтому

Для строго доказательства того, что предел , разделим числитель и знаменатель дроби на (величину, определяющую «скорость стремления знаменателя на бесконечность»).

Принимая во внимание, что

, и

в результате получим, что

Данный предел уже не содержит « неопределённости» и для его вычисления применим теорему о пределе частного двух функций.

Учитывая, что при , окончательно получаем

Ответ: предел .

Следующие два предела № 5в и № 5г содержат неопределённость вида и учебной программой предполагается, что они вычисляются с помощью замены бесконечно малых функций на эквивалентные.

Напомним, что функция называется бесконечно малой функцией в точке , если .

Две бесконечно малые функций и в точке называются эквивалентными, если и пишут .

При вычислении предела отношения бесконечно малых функций будем использовать следующую теорему.

Теорема. Пусть , , , суть бесконечно малые функции в точке , причём и . Тогда, если существует один из пределов

, , то существует и второй, и они равны

Напомним наиболее часто встречающиеся соотношения эквивалентности:

где может быть как независимой переменной, стремящейся к нулю, так и бесконечно малой функцией в точке .