Решение задачи № 1
Найдём координаты векторов
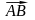и
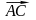по формуле (3):
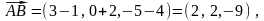
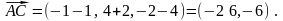
Используя
формулы (4), сначала находим координаты
вектора
,
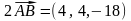затем координаты вектора
.
Скалярное
произведение векторов
и
вычисляем по формуле (6):
Векторное произведение векторов
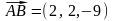и
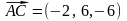находим по формуле (10):
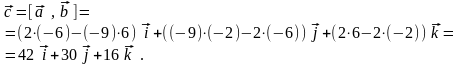
Таким
образом, получаем, что
.
Из определения векторного произведения следует, что площадь
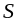параллелограмма, построенного на
векторах
и равна длине векторного произведения, т. е.
.
Для определения длины вектора воспользуемся формулой (2):
Ответ:
;
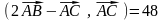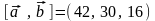;площадь параллелограмма, построенного на векторах и равна
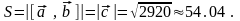
Решение задачи № 2
Так как плоскость
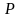проходит через точку
,
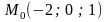то её уравнение будем искать в виде
(12):
В
нашей задаче
,
и
.
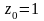В качестве вектора нормали плоскости можно взять любой ненулевой вектор, перпендикулярный плоскости .
Так
как плоскость
параллельна плоскости
,
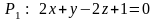то их нормальные векторы коллинеарны
,
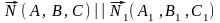поэтому в качестве вектора нормали
можно взять вектор
(вектор
нормали
плоскости
),
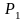т. е.
.
Тогда уравнение искомой плоскости примет вид
или
.
Найдём угол между двумя плоскостям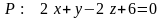и
и
.
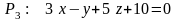Углом между двумя плоскостями, заданными уравнениями
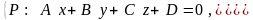
будем
называть любой из двугранных углов,
образованных этими плоскостями. Один
из этих углов равен углу
между нормальными векторами
и
плоскостей
и
,
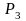соответственно. Угол
определяется согласно формуле (7), а
именно:
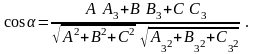
В нашей задаче получаем, что
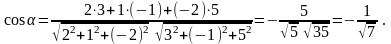
и
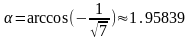радиан или
.
Ответ:
уравнение искомой плоскости ;
,
.
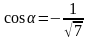Решение задачи № 3
Две прямые параллельны тогда и только тогда, когда параллельны их направляющие векторы. Найдём направляющие векторы данных прямых.
Первая прямая задана параметрическими уравнениями. В этом случае координатами направляющего вектора являются коэффициенты при параметре (см. (15)). Следовательно, направляющий вектор первой прямой
.Вторая прямая задана как линия пересечения двух плоскостей:
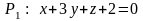с вектором нормал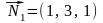и
и
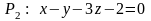с вектором нормали
.
Любой
вектор, перпендикулярный векторам
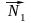и
,
параллелен данной прямой и, следовательно,
является её направляющим вектором.
Поэтому в качестве направляющего вектора
второй прямой можно взять вектор
.
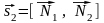С
помощью формулы (10) найдём координаты
вектора
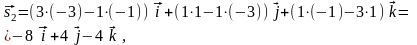
Таким
образом,
.
Докажем параллельность векторов
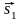и
,
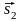используя условие (11):
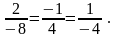
Справедливость последних равенств доказывает параллельность данных прямых.
Ответ: прямые параллельны.
Решение задачи № 4
Найдём
параметрические уравнения прямой.
Учитывая, что точка
лежит на прямой, уравнения (15) перепишем
в виде:
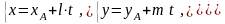
Так
как прямая перпендикулярна плоскости
,
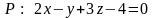то в качестве направляющего вектора
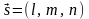прямой можно взять вектор нормали
плоскости
,
т. е.
.
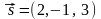Подставляя координаты точки
и направляющего вектора
в параметрические уравнения прямой,
получаем
Ответ:
