Примерный вариант контрольной работы № 2 по векторной алгебре, аналитической геометрии в пространстве и пределам

Каждый вариант контрольной работы № 2 содержит четыре задачи на тему «Векторная алгебра» и ее приложение к аналитической геометрии в пространстве и четыре примера на тему «Вычисление пределов функций».

1. Даны три точки , и . Найти:

1) скалярное произведение ; 2) векторное произведение ; 3) площадь параллелограмма, построенного на векторах и .

2. Составить уравнение плоскости, проходящей через точку и параллельной плоскости . Найти угол между этой плоскостью и плоскостью .

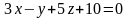3. Доказать параллельность прямых

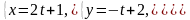и

4. Составить уравнение прямой, проходящей через точку перпендикулярно плоскости .

5. Найти пределы:

а) ; б) ;

в) ; г)

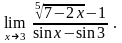
Прежде чем приступать к решению задач, Вам необходимо ознакомиться с «Рабочей программой» и изучить соответствующий т еоретический материал по учебникам, указанным в разделе «Рекомендуемая литература».

Для решения первых четырех задач потребуется знание основных понятий векторной алгебры и ее приложений к аналитической геометрии в пространстве [1–3, 6].

Приведем основные понятия и формулы, используемые

Рис. 6 при решении задач 1–4.

1. Мы предполагаем, что в пространстве введена правая декартова система координат и декартов базис 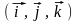, изображённые на рис. 6. Направление единичных векторов совпадает с направлением декартовых осей координат , , , соответственно. Обозначим проекции вектора на координатные оси через , и , тогда вектор однозначно представляется в виде

. (1)

Декартов базис позволяет установить взаимно однозначное соответствие между векторами и тройками чисел . Представление вектора в виде и в виде считаем эквивалентными. Числа , и называются координатами вектора в базисе .

2. Длина вектора 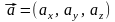определяется по формуле

(2)

3. Если даны координаты начала и конца вектора , то координаты вектора вычисляются по формулам:

, и (3)

4. Если даны координаты векторов , и число , то

(4)

5. Скалярным произведением двух векторов и 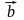называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение двух векторов и будем обозначать символом , тогда по определению

(5)

Имеет место следующее утверждение.

Если и , то

(6)

Из формул (5) и (6) следует, что

(7)

Замечание. Если векторы и перпендикулярны , то угол , и скалярное произведение этих векторов равно нулю:

(8)

6. Векторное произведение. Напомним, что в трехмерном векторном пространстве выбран правый ортонормированный базис , изображённый на рис. 6 и 7. Выбор базиса, который по определению считается правым, равносилен ориентации пространства. Будем говорить, что векторы образуют правую тройку.

Определение векторного произведения двух векторов включает в себя выбор ориентации пространства.

Векторным произведением двух упорядоченных векторов и называется новый вектор 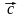, удовлетворяющий следующим условиям:

1. вектор перпендикулярен векторам и ;

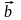2. направление вектора выбирается так, чтобы тройка векторов образовывала правую тройку;

3. длина вектора численно равна площади 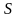параллелограмма, построенного на векторах и , приведённых к общему началу. Пусть - угол между векторами

4. и , тогда

(9)

Векторное произведение будем обозначать символом .

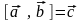Рис. 7

Для определения направление вектора удобно применять также правило «правой руки»: если векторы , и приведены к общему началу, то вектор должен быть направлен так, как направлен средний палец правой руки, большой палец которой направлен по первому сомножителю (т. е. вектору ), а указательный – по второму сомножителю (т. е. вектору ). Это правило чаще всего используется для определения направления вектора .

Имеют место следующие утверждения.

Если известны координаты векторов и , то координаты векторного произведения этих векторов определяются по формуле

(10)

Если векторы и коллинеарны (введём для них обозначение ), то . Иногда коллинеарные векторы называют параллельными. В координатной форме условие коллинеарности выглядит так:

(11)

т. е. координаты коллинеарных векторов пропорциональны.

7. Уравнение плоскости, проходящей через точку перпендикулярно вектору , имеет вид

(12)

Вектор называется вектором нормали к плоскости.

Если в уравнении (12) раскрыть скобки, перегруппировать члены и ввести обозначение , то получим уравнение

(13)

которое называется общим уравнением плоскости.

Обращаем Ваше внимание, что координаты вектора нормали являются коэффициентами при переменных , и в общем уравнении плоскости (13).

7. Канонические уравнения прямой, проходящей через точку параллельно вектору , имеют вид

(14)

Вектор называется направляющим вектором прямой.

Параметрические уравнения прямой получаются из уравнений (14) введением параметра , следующим образом:

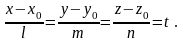
Приравнивая в отдельности каждую дробь параметру и разрешая полученные уравнения относительно переменных , и , получаем параметрические уравнения прямой

(15)

Обращаем Ваше внимание, что координаты направляющего вектора прямой являются коэффициентами при параметре в уравнениях (15).

Также из уравнений (14) видно, что прямая в пространстве может быть задана как линия пересечения двух плоскостей, т. е. в виде

(16)