Решение задачи № 3
Мы приведем два способа решения этой задачи.
Первый способ.
1.
Найдем фокус параболы
.
Для этого запишем уравнение параболы
в каноническом виде:
,
здесь
–параметр
параболы. В результате получаем:
и
.
Фокус параболы находится в точке
,
т. е. в точке
.
2. Найдем уравнение асимптоты гиперболы , проходящей через и квадранты. Для этого представим наше уравнение гиперболы в каноническом виде:
,
где – вещественная полуось и –мнимая полуось. Получаем уравнение
,
в
котором
и
.
Уравнение
асимптоты гиперболы, проходящей через
и
квадранты, имеет вид:
,
в нашей задаче имеем
.
Сделаем рисунок.
Рис. 4
3.
Пусть точка
является основанием перпендикуляра,
опущенного из точки
на прямую
.
Найдем
уравнение прямой
,
перпендикулярной прямой
.
Так как угловой коэффициент прямой
равен
,
то
.
Уравнение
прямой
ищем в виде
.
В результате получаем, что
:
или
.
4. Найдем координаты точки . Точка является точкой пересечения двух прямых и , поэтому ее координаты будут решением системы уравнений:
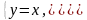
решая
которую, получим
,
.
Таким образом,
.
5. Найдем расстояние от точки до прямой :
Ответ:
расстояние от фокуса параболы до
асимптоты гиперболы равно
.
Второй способ.
Выполним
пункты 1 и 2 решения задачи первым
способом. В результате найдем координаты
фокуса параболы
и уравнение асимптоты гиперболы,
проходящей через
и
квадранты,
.
3.
Для нахождения расстояния
от точки
до прямой
воспользуемся следующей формулой:
В
нашей задаче:
,
,
,
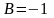и
.
Подставляя в приведенную формулу эти значения, получаем:
Ответы при решении задачи первым и вторым способами, конечно, совпадают.
Решение задачи № 4
Чтобы
привести уравнение
к
каноническому виду, мы воспользуемся
методом выделения полных квадратов по
переменным
и
,
и параллельным переносом декартовой
системы координат.
Для
выделения полных квадратов следует
применить формулу
.
1. Выделим в данном уравнении полные квадраты. Для этого сгруппируем отдельно слагаемые, содержащие и :
.
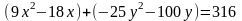Вынесем
за скобки коэффициенты при
и
:
.
Дополним выражения в скобках до полного квадрата разности и суммы:
Разделив
обе части этого уравнения на
,
получим:
2.
Чтобы последнее уравнение приняло
канонический вид, введем новые переменные
и
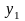по формулам:
Этим
формулам соответствует параллельный
перенос старой системы координат
в
новую систему координат
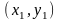с началом в точке
.
В новой системе координат получаем каноническое уравнение гиперболы
с
полуосями
и
.
3. Сделаем чертеж (рис. 5).
Для
этого в канонической системе координат
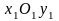строим характеристический прямоугольник
гиперболы со сторонами, параллельными
осям координат
и
.
Точка пересечения диагоналей совпадает
с началом координат
и длины сторон прямоугольника равны
и
.
Прямые, на которых лежат диагонали
прямоугольника, являются асимптотами
для ветвей гиперболы. Вершины гиперболы
будут находиться в точках
и
.
Из уравнения гиперболы видно, что она
обладает симметрией относительно осей
координат
,
и начала координат
.
После
этого рисуем ветви гиперболы. Далее
строим старую систему координат
с осями
и
,
параллельными осям координат
и
,
соответственно, центр которой находится
в точке
.
Ответ: заданному уравнению соответствует гипербола с каноническим уравнением:
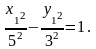
Гипербола изображена на рис. 5.
Рис. 5