
- •Г. В. Красоленко, н. В. Сванидзе, г. В. Якунина аналитическая геометрия. Векторная алгебра. Теория пределов
- •Введение
- •Элементы векторной алгебры и линейной аналитической геометрии в пространстве
- •Функция одной переменной, ее предел и непрерывность
- •Примерный вариант контрольной работы № I по аналитической геометрии на плоскости
- •Решение задачи № 1
- •Решение задачи № 2
- •Решение задачи № 3
- •Решение задачи № 4
- •Примерный вариант контрольной работы № 2 по векторной алгебре, аналитической геометрии в пространстве и пределам
- •Решение задачи № 1
- •Решение задачи № 2
- •Решение задачи № 3
- •Решение задачи № 4
- •Решение задачи № 5 а
- •Решение задачи № 5 б
- •Решение задачи № 5 в
- •Решение задачи № 5 г
- •Контрольная работа № 1 по аналитической геометрии на плоскости
- •Контрольная работа № 2 по векторной алгебре, аналитической геометрии в пространстве и пределам
- •Рекомендуемая литература
- •Оглавление
- •Аналитическая геометрия. Векторная алгебра. Теория пределов
- •190005, Санкт-Петербург, 2-я Красноармейская ул., д. 4.
Примерный вариант контрольной работы № I по аналитической геометрии на плоскости
1.
Даны координаты двух противоположных
вершин ромба
 ,
,
 и уравнение стороны
и уравнение стороны
 .
Найти координаты вершин ромба
.
Найти координаты вершин ромба
 и
и
 .
.
2.
Найти каноническое уравнение эллипса
и построить кривую, если его малая
полуось равна радиусу окружности
 ,
а левый фокус совпадает с центром другой
окружности
,
а левый фокус совпадает с центром другой
окружности
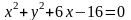 .
.
3.
Найти расстояние от фокуса параболы
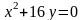 до асимптоты гиперболы
до асимптоты гиперболы
 ,
проходящей через
,
проходящей через
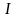 и
и
 квадранты.
квадранты.
4.
Привести уравнение
 к каноническому виду. Построить кривую,
соответствующую этому уравнению.
к каноническому виду. Построить кривую,
соответствующую этому уравнению.
Мы рекомендуем при решении задач контрольной работы № 1 делать рисунки в декартовой системе координат. Они, в некоторой степени, будут контролем правильности решения Вашей задачи.
Решение задачи № 1
1. Сделаем рисунок и запишем краткое условие нашей задачи.

Рис. 1
Так
как координаты точки
удовлетворяют уравнению
,
то точка
 принадлежит этой прямой и можно считать,
что сторона ромба
принадлежит этой прямой и можно считать,
что сторона ромба
 лежит на этой прямой.
лежит на этой прямой.
Дано:
 –
ромб;
,
;
–
ромб;
,
;

Найти координаты точек и .
2.
Найдем координаты точки
,
которая является серединой отрезка
 (см. рис.1). Следовательно,
(см. рис.1). Следовательно,

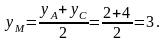
Таким
образом,
 .
.
3. Найдем угловой коэффициент диагонали по формуле

4.
Составим уравнение диагонали
 .
Так как диагонали ромба перпендикулярны,
то их угловые коэффициенты связаны
соотношением
.
Так как диагонали ромба перпендикулярны,
то их угловые коэффициенты связаны
соотношением
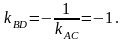
Итак,
нам известны координаты точки
,
лежащей на диагонали
,
и ее угловой коэффициент
 .
Используя уравнение пучка прямых
.
Используя уравнение пучка прямых
 ,
составим уравнение диагонали
:
,
составим уравнение диагонали
:
 .
.
Отсюда
получаем общее уравнение диагонали
:
 .
.
5. Найдем координаты точки как точки пересечения двух прямых и , т. е. координаты точки являются решением следующей системы линейных уравнений:

Для
нахождения решения этой системы вычтем
из первого уравнения второе, получим:
 .
Подставляя
в первое уравнение, находим вторую
компоненту решения
.
Подставляя
в первое уравнение, находим вторую
компоненту решения
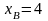 .
Таким образом, координаты точки
.
Таким образом, координаты точки
 .
.
6. Найдем координаты точки . Так как точка делит отрезок пополам, то
 и
и


Отсюда получаем:
 и
и
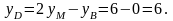
Следовательно,
координаты точки
 .
.
Ответ: и .
Решение задачи № 2
Каноническое уравнение эллипса имеет вид

где
 –длина
большой полуоси,
–длина
большой полуоси,
 –длина
малой полуоси и координаты фокусов
–длина
малой полуоси и координаты фокусов
 и
и
 (см. рис. 2). Параметры эллипса
,
и
(см. рис. 2). Параметры эллипса
,
и
 принимают положительные значения и
связаны следующим соотношением
принимают положительные значения и
связаны следующим соотношением
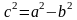

Рис. 2
1.
Найдем радиус окружности
.
Для этого, используя формулу
 ,
приведём наше уравнение окружности к
каноническому виду:
,
приведём наше уравнение окружности к
каноническому виду:

где
точка
 является центром окружности, а
является центром окружности, а
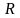 -радиусом.
-радиусом.
Сначала
перепишем заданное уравнение окружности
в следующем виде
 ,
затем выделим полный квадрат по переменной
,
затем выделим полный квадрат по переменной
 :
:
 .
В результате получаем
.
В результате получаем
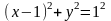 .
Следовательно, радиус окружности
.
Следовательно, радиус окружности
 и параметр эллипса
и параметр эллипса
 .
.
2.
Найдем центр окружности
.
В этом уравнении перегруппируем
слагаемые, стоящие в левой части, и так
же, как в первом пункте, выделим полный
квадрат по переменной
:
 и
и
 .
Отсюда центр окружности имеет координаты
.
Отсюда центр окружности имеет координаты
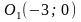 .
Следовательно, левый фокус эллипса
находится в точке
.
Следовательно, левый фокус эллипса
находится в точке
 и параметр эллипса
и параметр эллипса
 .
.

Рис. 3
3.
Найдем параметр эллипса
с помощью соотношения
 ,
т. е.
,
т. е.
 .
.
Таким
образом, искомое уравнение эллипса
имеет вид

Ответ:
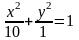 и эллипс изображен на рис. 3.
и эллипс изображен на рис. 3.
