
- •Задача №12.
- •Задача №17.
- •Iн − ток полного отклонения (номинальный ток).
- •Задача №35.
- •1.22. Охарактеризуйте (поясните сущность, укажите основные признаки, приведите примеры применения, осветите технико-экономические стороны) каждый из существующих методов стандартизации.
- •2.17 Сформулируйте правила суммирования систематических погрешностей.
- •Литература
2.17 Сформулируйте правила суммирования систематических погрешностей.
Каждый
параметр может иметь отклонение xi
(погрешность) от предписанного значения
xi. Поскольку погрешность xi
мала по сравнению с величиной xi, суммарная
погрешность y
функции y можно вычислять по формуле
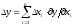 ,
,
где y/xi - передаточное отношение (коэффициент влияния) параметра xi.
Формула справедлива лишь для систематических погрешностей xi.
Для случайных погрешностей (когда отдельные составляющие не всегда принимают предельные значения) используются теоремы теории вероятностей о дисперсии, то есть
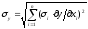
Суммарная погрешность при наличии только случайных составляющих xi погрешностей
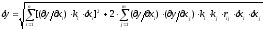 ,
,
где m - число попарно корреляционно связанных параметров;
ki и kj - коэффициенты относительного рассеяния, характеризующие степень отличия закона распределения погрешности данного параметра от нормального;
rij - коэффициент корреляции, существующий при наличии корреляционной связи между параметрами xi и xj.
При наличии и систематических и случайных составляющих погрешностей вычисляют доверительные границы суммарной погрешности:
yсум = y ky ,
где k - масштабный коэффициент интервала распределения, зависящий от закона распределения и принятой доверительной вероятности. Так, при доверительной вероятности Р = 0,95 для закона нормального распределения k = 2, а для закона Максвелла k = 3,6.
Рассчитываем доверительные границы случайной погрешности результата измерения:

t - коэффициент Стьюдента
Определяем доверительные границы неисключенной систематической погрешности результата измерения:
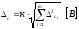
где m − число суммируемых погрешностей;
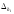 − граница
i-ой неисключенной погрешности;
− граница
i-ой неисключенной погрешности;
к
− коэффициент, определяемый принятой
доверительной вероятностью При
доверительной вероятности Рд
= 0,99 коэффициент k принимают равным 1,4,
если число суммируемых неисключенных
систематических погрешностей более
четырёх (m >4). Если число суммируемых
погрешностей m4,
то коэффициент k определяют по графику
зависимости (рисунок) k=f(m, l), где m - число
суммируемых погрешностей;
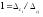 ;
кривая 1 - для m =2; кривая 2 - для m = 3; кривая
3 - для m = 4.
;
кривая 1 - для m =2; кривая 2 - для m = 3; кривая
3 - для m = 4.
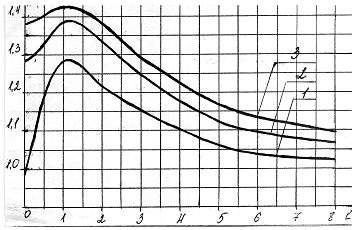
График зависимости k = f(m, l).
При
трёх или четырёх составляющих в качестве
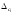 принимают составляющую, по числовому
значению наиболее отличающуюся от
других. В качестве
принимают составляющую, по числовому
значению наиболее отличающуюся от
других. В качестве
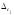 следует принять ближайшую к
следует принять ближайшую к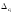 составляющую.
составляющую.
Вычислим алгебраическую сумму систематических погрешностей:
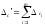
За
оценку неисключенной систематической
погрешности принимаем то из значений
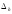 ,
которое меньше.
,
которое меньше.
Найдем
отношение:
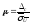 .
.
В
случае если <
0,8, то неисключенными систематическими
погрешностями по сравнению со случайными
пренебрегают и принимают, что граница
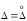 .
Если >
8, то пренебрегают случайной погрешностью
по сравнению с систематическими и
принимают, что граница погрешности
результата
= с.
.
Если >
8, то пренебрегают случайной погрешностью
по сравнению с систематическими и
принимают, что граница погрешности
результата
= с.
Погрешность, возникающая из-за пренебрежения одной из составляющих погрешности результата измерения при выполнении указанныx неравенств, не превышает 15 %.
Если лежит в интервале от 0,8 до 8, начит, граница погрешности результата будет [2]:
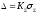 ,
,
Где
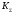 – коэффициент, зависящий от соотношения
случайной и неисключенной систематической
погрешностей.
– коэффициент, зависящий от соотношения
случайной и неисключенной систематической
погрешностей.
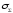 – оценка
суммарного среднего квадратического
отклонения результата измерения.
– оценка
суммарного среднего квадратического
отклонения результата измерения.
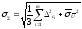
Коэффициент
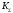 вычисляют по эмпирической формуле:
вычисляют по эмпирической формуле:
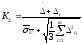
Определим доверительные границы суммарной погрешности результата измерения:
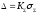
Доказывается,
что с погрешностью не более 10% значение
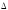 может быть определено по более простой
формуле:
может быть определено по более простой
формуле:
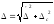
[2,5]
