Физика 1 часть КР 1 вариант 1
.docxБЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра программного обеспечения информационных технологий
Факультет НиДО
Специальность ПОИТ
Контрольная работа № 1
по дисциплине «Физика» часть 1
Вариант № 1
Выполнил студент: Тарасевич М.А.
группа
Зачетная книжка №
Минск 2011
101) Задача
Уравнение движения частицы х = 4+2t-0,6t3 м. Найти координату, скорость и ускорение при t= 4 с.
Решение
-
Координата точки в момент времени t = 4c будет равна
x = 4+2*4-0.6*43 = -26.4 (м)
-
Определим зависимость сокрости от времени Vx, так как
x = 4+2t-0,6t3 м
Vx
=
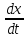 =
=
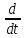 (4+2t-0.6t3)
= 2 – 1.8t2
= 2-1.8*42
= -26.8 (м/с).
(4+2t-0.6t3)
= 2 – 1.8t2
= 2-1.8*42
= -26.8 (м/с).
-
Зависимость ускорения от времени найдем по формуле
ax
=
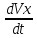 =
=
 (2 – 1.8t2)
= -3.6t
= -3.6t*4
= -14.4 (м/с2).
(2 – 1.8t2)
= -3.6t
= -3.6t*4
= -14.4 (м/с2).
Ответ: x = -26.4 (м), Vx = -26.8 (м/с), ax = -14.4 (м/с2).
111) Задача
Точка движется по прямой с ускорением а = 0.5V. Найти зависимость скорости от времени, определить скорость через 4с после начала движения, V0 = 2 м/с.
Решение
-
Ускорение точки a =
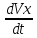 ,
то есть
,
то есть
 = 0.5V
= 0.5V -
Решим дифферинциальное уравнение
 = 0.5dt
= 0.5dt -
Проинтегрируем
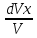 = 0.5dt
= 0.5dt
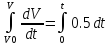
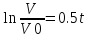
V(t) = V0 * e0.5t
-
Скорость точки в момент времени t = 4c
V = 2 * e0.5*4 = 14.8 (м/с)
Ответ: V(t) = V0 * e0.5t, V = 14.8 (м/с).
121) Задача
Тело
движется по окружности радиусом 1 м и
S= м. Найти массу тела, если при S = 2 м модуль
действующей силы равен 5 Н.
м. Найти массу тела, если при S = 2 м модуль
действующей силы равен 5 Н.
Решение
-
Определим скорость тела
V
=
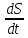 =
=
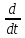 (
(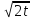 )
=
)
=

-
Согласно II закону Ньютона
F = man
-
Центростремительное ускроение будет равно
an
=
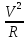
-
Подставим значения
F
= m
-
Отсюда масса тела m равна
m = 2tRF
-
Найдем момент времени, в который S = 2м
t
=
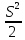
-
Подставим полученное значение
m
=
 = 22*1*5
= 20 (кг)
= 22*1*5
= 20 (кг)
Ответ: m = 20 (кг).
131) Задача
Две частицы, движущиеся со скоростями Vi = 2i +13j и V2 = 4i – 5j, сталкиваются друг с другом, в результате чего образуется составная частица. Найти модуль скорости образовавшейся частицы, если массы частиц одинаковы. Скорости частиц выражены в метрах в секунду.
Решение
-
В данном случае систему можно считать замкнутой, следовательно можно воспользоваться законом сохранения импульса
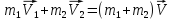
-
Запишем уравнение в проекциях на оси
ox:
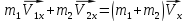
oy:
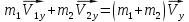

-
Так как m1 = m2, то с учетом этого уравнения примут вид
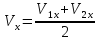
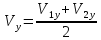
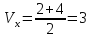 (м/с)
(м/с)
 (м/с)
(м/с)
-
Модуль скорости будет равен
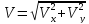
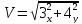 =
5 (м/с)
=
5 (м/с)
Ответ:
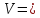 5 (м/с).
5 (м/с).
141) Задача
Из космического пространства на Землю падает метеорит массой 2 кг. Найти работу сил гравитационного поля. Радиус Земли принять равным 6400 км.
Решение
-
Работа сил гравитационного поля рассчитывается по формуле
 ,
,
где U1 и U2 – потенциал гравитационного поля
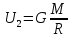
так
как
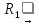 ∞ , то
∞ , то
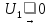
-
Подставим значения, учтя при этом, что U1 = 0

 (Дж)
(Дж)
Ответ:
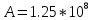 (Дж).
(Дж).
151) Задача
Нить с грузами на концах 0,3 и 0,5 кг перекинута черве блок диаметром 10 см, который вращается угловым ускорением 4 род-с-2. Найти момент инерции блока.
Решение
y
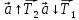



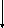

y
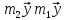
-
Воспользуемся основным уравнением динамики вращательного движения
 , где
, где
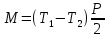 – момент внешних сил, действующих на
блок
– момент внешних сил, действующих на
блок

-
Рассмотрим силы, действующие на груз m2. Согласно II закону Ньютона
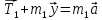
или в проекции на ось oy
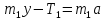
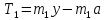
-
Рассмотрим силы, действующие на груз m1. Согласно II закону Ньютона

или в проекции на ось oy


-
Подставим значения T1 и T2
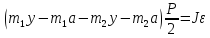

-
Ускорение грузов

-
Подставим значение a

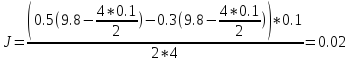 (кг*м2)
(кг*м2)
Ответ:
 (кг*м2).
(кг*м2).
161) Задача
Найти момент инерции обруча массой m и радиусом R относительно оси, проходящей через диаметр обруча.
Решение
dx
r

α


-
Выделим на ободе элемент dx, массой dm = rdx.
-
Момент инерции элемента dx относительно оси
dI = dm*22,
где r = R*sin α
dI = dm*R2*sin2 α
dI = r*R2*sin2 α*dα
dx = R*dα
dI = r*R3*sin α* dα
-
Для нахождения момента инерции полукольца проинтегрируем
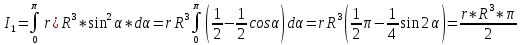
-
Масса половины обруча
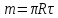
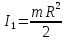
-
Момент инерции обруча
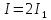

Ответ:
 .
.
171) Задача
На вращающейся скамье Жуковского = 8 рад/с стоит человек со стержнем длиной 2 м, массой 10 кг. Найти угловую скорость и произведенную работу, если стержень, стоящий вертикально по оси скамьи повернуть горизонтально. симметрично оси. Суммарный момент инерции скамьи и человека равен 4 кг-м2.
Решение
-
В данном случае систему человек-скамья-стержень можно считать замкнутой. Следовательно можно воспользоваться законом сохранения момента импульса
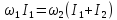 ,
,
где
 - момент инерции стержня.
- момент инерции стержня.
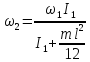
 (рад/ч)
(рад/ч)
-
Произведенную работу найдем, воспользовавшись теоремой о кинетической энергии
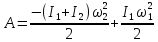
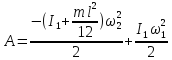
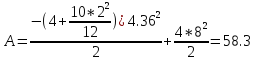 (Дж)
(Дж)
Ответ:
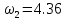 (рад/ч),
(рад/ч),
 (Дж).
(Дж).