1. Энергия магнитного поля. Энергия электрического поля. Объемная плотность энергии магнитного поля. Объемная плотность энергии электрического поля.

Пусть в контуре с индуктивностью L течет ток силой I₀ в момент размыкания цепи возникает индукционный ток ( в следствие самоиндукции) и будет совершена некоторая работа А.Очевидно, эта работа может быть совершена только за счет энергии исчезнувшего при размыкании цепи магнитного поля, связанного с контуром, т.е. энергия исчезнувшего магнитного поля переходит в энергию индукционного электрического поля, за счет которой и совершается работа А.

Вычислим работу за время dt:

г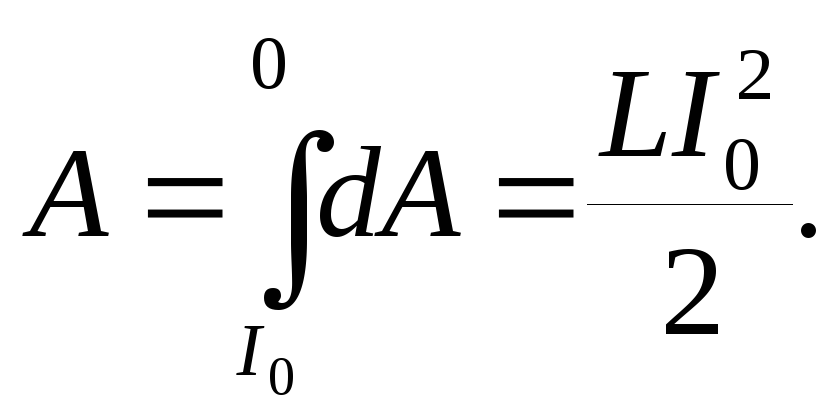деε - э.д.с. самоиндукции; так как , тооткуда

Однако эта работа, как было сказано, совершается за счет энергии магнитного поля, связанного с контуром, следовательно, энергия магнитного поля

Рассчитаем энергию магнитного поля достаточно длинного соленоида. Подставляя в эту формулу значения L из ( 191а) и , получаем

Плотность энергии магнитного поля, т.е.энергия, приходящаяся на единицу его объема, равна

Величина, опр-мая отношением энергии потен к единице оьъема наз объемной плотностью энергии

W_p / V = w [Дж/м²] w=0,5*e₀*e*E²=0,5*ДЕ, Д – эл смещение

Энергия эл поля

2. Токи смещения.

Величина (это величина, по размерности равная плотности тока) называетсятоком смещения. Название принадлежит Максвеллу, название осталось, а аргументация пропала: ничего там не смещается, и название «ток смещения» не должно вызывать в вас никаких ассоциаций с тем, что там что-то смещается, это термин, который остался по историческим причинам.

Мораль такая: переменное электрическое поле само по себе создаёт магнитное поле. И всё замыкается! Переменное магнитное поле является источником электрического, переменное электрическое поле является источником магнитного, и уравнения в вакууме приобретают симметричный вид (отличие только в знаке перед производной, но это не столь страшное нарушение симметрии).

В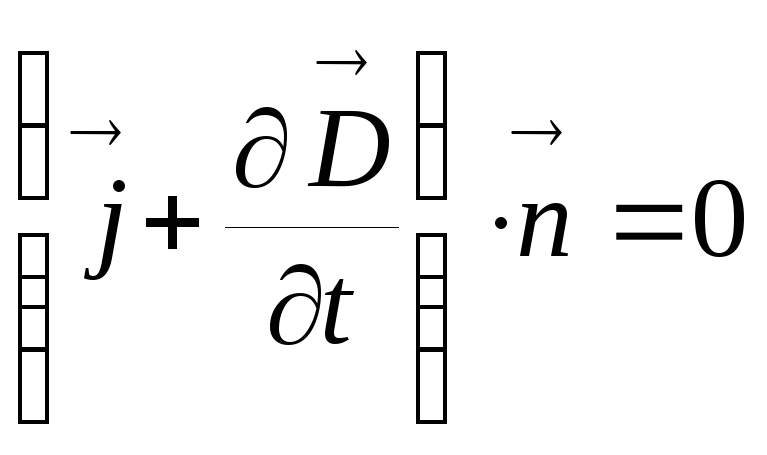ведение этого тока смещения в первом примере спасает дело: на этой картинеи .

Короче говоря, циркуляция по любому контуру – ноль. Таким образом, четвёртое уравнение для этого сферически симметрично растекающегося тока даёт, что магнитное поле равно нулю. Эта Максвелловская поправка навела порядок, и теория стала непротиворечивой.

3. Уравнение максвелла в интегральной форме

Первая пара уравнений Максвелла :

Первое из этих уравнений связывает значения Е с временными изменениями вектора В и является по существу выражением закона электромагнитной индукции. Второе уравнение отражает то свойство вектора В, что его линии замкнуты (или уходят в бесконечность).

Вторая пара:

J – плотность тока проводимости. 1 уравнение устанавливает связь между токами проводимости и смещения и порождаемым ими магнитным полем. 2 показывает, что линии вектора D могут начинаться и оканчиваться на зарядах.

Уравнения 1-4 представляют собой уравнения Максвелла в интегральной форме. Они связывают значения Е или Н вдоль некоторого контура со значениями В (соот-но D) в точках опирающейся на контур поверхности. От уравнений в интегральной форме можно с помощью теорем векторного анализа перейти к уравнениям в диф форме, кот связываю значения Е или Н в некот точке с В (соот-но D) в той же самой точке прост-ва.

4. Электромагнитное поле и его материальность.

Переменное магн поле всегда связано порождаем им Эл полем, в свою очередь переменное Эл всегда связано с порождаемым им магнитным. Т.о., Эл и магн поля оказываются неразрывно связанными друг с другом – они образуют единое электромагнитное поле.

Электростатическое поле создается системой неподвижных зарядов. Однако, если заряды неподвижны относительно некот инерциальной системы отсчета, то относительно др инерц систем эти заряды движутся и, сл-но, будут порождать не только Эл-кое, но и магн поле (движущийся заряд эквивалентен току). Неподвижный провод с пост током создает в каждой точке прост-ва пост магн поле. Однако отн-но др инерц-х систем этот провод нах-ся в движении. Поэтому создаваемое им магн поле в любой точке с заданными корд-тами x, y, z будет меняться и, сл-но, порождать вихревое Эл поле. Т.о., поле, кот относительно некот системы отсчета оказывается «чисто» Эл-ким или «чисто» магнитным, относ-но др систем отсчета будет собой представлять собой совокупность Эл и магнитного полей.

5. Общий признак колебательного движения. Гармонические колебания, и их общая характеристика. Дифференциальное уравнение гармонически колеблющихся систем и его решение.

Колебания – движение в той или иной степени, повторяющиеся во времени (т. е. повторяемость во времени величин, описывающих это движение).

Колебания: свободные (незатухающ., затухающ.), вынужден (незатухающ).

Свободные колебания – колебания, которые совершат система, выведенная из состояния устойчивого равновесия и представленная самой себе.

Вынужденные колебания – колебания, которые происходят под периодическим действием внешней силы.

Гармонические колебания – колебания, которые происходят по закону sin или cos.

Характеристики: А – амплитуда – максимальное значение по модулю функции за период; Т – период – время одного полного колебания; ν – частота – число колебаний в единицу времени. ν = 1/Т; ω – циклическая частота – число колебаний за 2π секунд. ω = 2πν рад/с; (ωt + φ₀) – фаза – величина, стоящая под знаком sin или cos и определяющая положение системы в данный момент времени. Величина, равная отношению фазы к 2π, показывает, какая доля периода прошла от начала колебаний. За время равное периоду фаза изменяется на 2π. φ₀ – начальная фаза – значение фазы в момент t = 0. Определяется начальными условиями и начальным положением системы.

Дифференциальное уравнение гармонических колебаний пружинного маятника: -kx=ma_x; ma_x+kx=0; ;; ω²=k/m; , гдеm-масса, k-коэффициент жесткости.

ДУ для физического маятника F_x=-kx; M=-amgα; ; ; ;

; ; ; ; , где I₀-момент инерции, a-расстояние от центра относительно оси, проходящей через центр масс до точки подвеса.

5. Энергия гармонического колебательного движения.

Колеблющаяся материальная точка обладает кинетической энергией

Так как скорость , то

( 204 )

В крайних положениях кинетическая энергия равна нулю, при прохождении положения равновесия она имеет максимальное значение.

Колеблющаяся точка обладает и потенциальной энергией. Потенциальная энергия точки, смещенная относительно положения равновесия на величину х, измеряется работой внешних сил, которая была произведена для того, чтобы вызвать это смещение, т.е.

Воспользовавшись формулами (198), (200а) и (203а), имеем

( 205 )

Следовательно, потенциальная энергия колеблющейся точки максимальна в крайних положениях и равна нулю в положении равновесия. Полная энергия равна

так как

Заменяя через, получим

т.е. энергия тела, совершающего гармоническое колебание, прямо пропорционально массе тела, квадрату амплитуды и квадрату частоты колебания.

5. Определение периодов колебаний систем с одной степенью свободы:пружинный маятник.

mg=kx0

k*∆x=F

m*x=-kx

x+w0x=0

x=Acos(w0t+φ0)?

5. Определение периодов колебаний систем с одной степенью свободы: математический маятник.

Математическим маятником называется тело массой m, размерами которого можно пренебречь, подвешенная на нерастяжимой и невесомой нити длинной l (рис. 182).

Когда нить висит вертикально, сила тяжести уравновешивается натяжением нити. Если нить отвести на некоторый угол, тог силаР уже не будет уравновешиваться натяжением нити. Разложим силу тяжести Р на две составляющее Р₁ и Р₂. сила Р₂ будет уравновешиваться натяжением нити, сила Р₁ будет возвращать маятник в положение равновесия; она равна

Если угол мал, то, следовательно,

Знак минус указывает, что сила Р₁ направлена в сторону, противоположную смещению.

Отсюда видно, что при небольших значениях угла силаР₁ пропорциональна смещению и, следовательно, при небольших амплитудах маятник будет совершать гармоническое колебание. Силы, которые по своем природе не являются упругими, но зависят от величины смещения относительно положении равновесия по такому же закону, как и упругие с илы, называются квазиупругими силами.

Сила Р₁ является примером квазиупругой силы.

Найдем период колебаний математического маятника. Из сравнения формул (203б) и (208) имеем

и окончательно

Из формулу (209) видно, что при небольших амплитудах период колебаний не зависит ни от самой амплитуды, ни от массы маятника.

5. Определение периодов колебаний систем с одной степенью свободы: физический маятник.

Любое твердое тело, могущее свободно вращаться вокруг неподвижной горизонтальной оси, не проходящий через его цент тяжести, называется физическим маятником (рис.183;0 – ось вращение, расположенная перпендикулярно чертежу, С – центр тяжести тела, l – расстояние от центра тяжести до оси вращения).

Если физический маятник вывести из положения равновесия, отклонив его на некоторый угол , то сила тяжестиР маятника можно разложить на две силы: Р₁ и Р_2. Пологая при небольших углах отклонения и учитывая направление силыР₁ , обратное отклонению маятника, можно записать

Момент силы Р₁ относительно оси вращения равен . Согласно второму закона Ньютона, для вращательного движения (см.§.28).

где- угловое ускорение;М – момент силы; J – момент инерции тела, или

( 210 )

т.е. угловое ускорение пропорционально угловому пути. Отсюда следует, что при небольших углах отклонение физический маятник будет совершать гармонические колебания.

Найдем период его колебаний. Для этого сравним формулу (202) и (210).

Из сравнения их следует, что

откуда, заменяя Р через , получаем