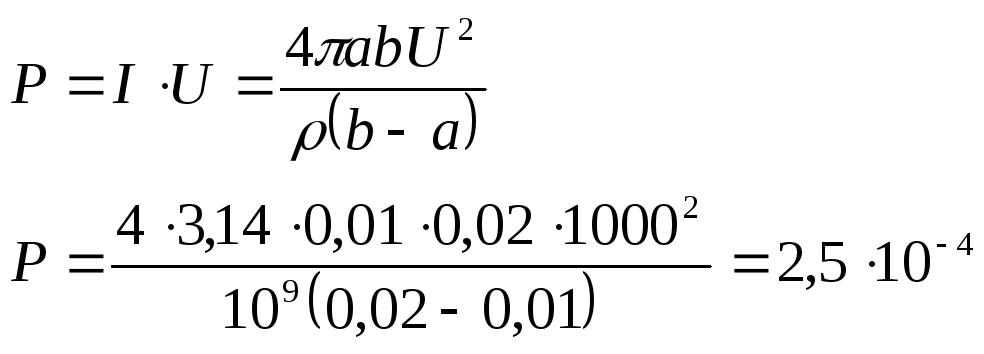физика,2 курс,3 сем.,4 вариант
.doc|
|
В
3 Дано: Решение: q1 = 3,2·10-9 Кл Заряды q1 и q2 будут действовать на заряд q3
q2
=-3,2·10-9
Кл
с силами
q3
= 4,6·10-9
Кл
F-? Результирующая сила
или по теореме косинусов, как видно из рисунка
Ответ:
3 Дано: Решение: R
= 5 см Выделим малый элемент
дуги окружности длиной
λ
и потенциал
Из
симметрии задачи ясно, что результирующая
напряжённость направлена по оси
симметрии четверти кольца
Результирующий потенциал в О:
Ответ:
3 Дано: Решение:
Т.к.
то вектор напряжённости
модуль вектора напряжённости:
Ответ:
334. Полый шар радиусом R равномерно заряжен с объемной плотностью ρ. Радиус полости R1 < R . Заряды внутри полости отсутствуют. Полагая диэлектрическую проницаемость внутри шара и вне его равной единице, найти напряженность поля как функцию расстояния r от центра шара: а) внутри полости; б) внутри шара; в) вне шара.
Д R,
R
при
при
при
Ответ:
3
ρ , R, ε Воспользуемся теоремой Остроградского-Гаусса для вектора
При
При
Тогда напряженность поля: при
при
Поляризованность диэлектрика
Поверхностная плотность связанных зарядов
Ответ:
при
354. Длинный цилиндр радиусом R = 1 см равномерно заряжен с линейной плотностью λ = 10–5 Кл/м. α-частица, попавшая в поле цилиндра, перемещается от поверхности цилиндра до точки, находящейся на расстоянии a = 4 см от его поверхности. Как при этом изменится кинетическая, потенциальная и полная энергия α-частицы?
R = 1см Напряжённость поля, создаваемую цилиндром на расстоянии r λ
= 10–5
Кл/м от его оси (
Следовательно, разность потенциалов, которую пройдёт α-частица:
Работа сил поля над α-частицей
Изменение потенциальной энергии α-частицы
Изменение кинетической энергии, согласно закону сохранения энергии:
Изменение полной энергии
Ответ:
364. Сколько ламп мощностью по N = 300 Вт каждая, рассчитанных на напряжение U = 100 В, можно установить в здании, если проводка от магистрали сделана медным проводом общей длиной ℓ = 100 м и сечением S = 9 мм2 и если напряжение в магистрали поддерживается равным U0 = 127 В?
Д N = 300 Вт Пусть ток через каждую лампу равен. Т.к. мощность лампы U
= 100 В
S
= 9 мм2
ℓ = 100 м Сопротивление проверки равно U n-?
Запишем
закон Ома для участка цепи, включающего
ламп:
Ответ:
374. Найти количество теплоты, выделяемой в единицу времени веществом с удельным сопротивлением 109 Ом·м, которое заполняет все пространство между двумя сферическими оболочками. Радиусы оболочек a = 1 см и b = 2 см, между ними поддерживается разность потенциалов U = 1000 В.
Д
a
= 1 см слоя радиуса r
и толщины
b
= 2 см электрическому
току
P-? Суммарное падение напряжения между сферическими оболочками
Отсюда
Ответ:
|
|

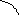 ариант
4
ариант
4 04.
В вершинах равностороннего треугольника
со стороной a = 14 см расположены
заряды q1
=
3,2·10-9
Кл, q2
= -3,2·10-9
Кл
и q3
= 4,6·10-9
Кл.
Найти величину и направление силы,
действующей на заряд q3.
04.
В вершинах равностороннего треугольника
со стороной a = 14 см расположены
заряды q1
=
3,2·10-9
Кл, q2
= -3,2·10-9
Кл
и q3
= 4,6·10-9
Кл.
Найти величину и направление силы,
действующей на заряд q3. a
= 14 см
a
= 14 см









 a
a
















 14.
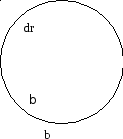
По четверти окружности радиусом R = 5
см равномерно распределен заряд с
линейной плотностью λ = 6·10-6
Кл/м.
Найти напряженность
14.
По четверти окружности радиусом R = 5
см равномерно распределен заряд с
линейной плотностью λ = 6·10-6
Кл/м.
Найти напряженность
 = 6·10-6
Кл/м
как показано на рисунке. Он создаёт
в центре О напряжённость
= 6·10-6
Кл/м
как показано на рисунке. Он создаёт
в центре О напряжённость ,
φ-?
x
,
φ-?
x



 φ
φ








 O
O



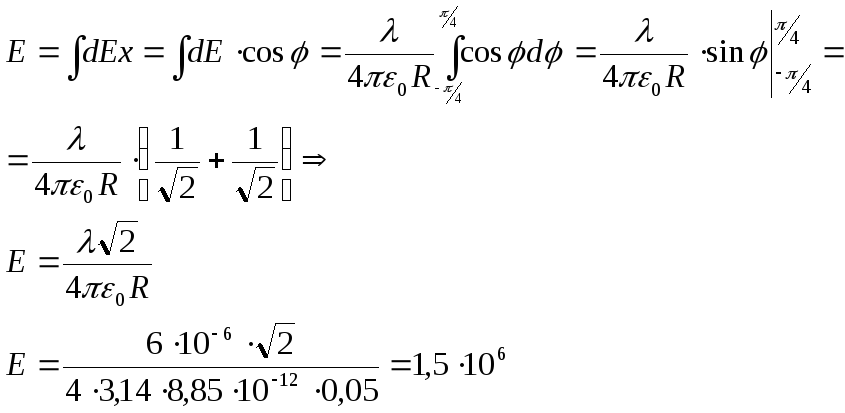

 24.
Потенциал некоторого электростатического
поля имеет вид:
24.
Потенциал некоторого электростатического
поля имеет вид:
 Связь
напряжённости электростатического
поля с
Связь
напряжённости электростатического
поля с








 ано:
Решение:
ано:
Решение: 1
<
R гауссовой поверхности выберем
концентрическую сферу радиуса r.
1
<
R гауссовой поверхности выберем
концентрическую сферу радиуса r.

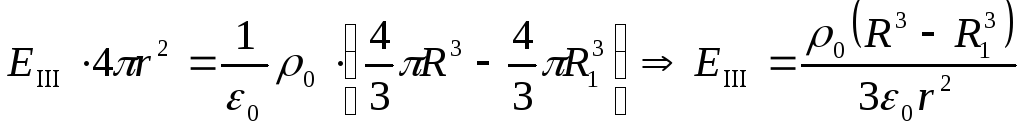
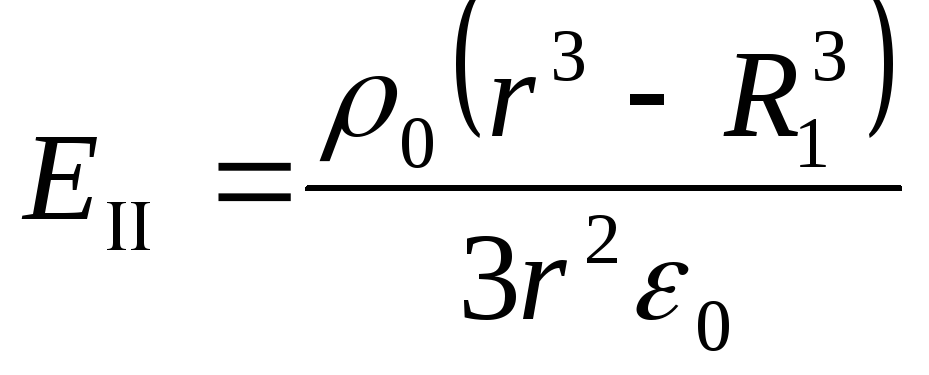 ,
,

 44.
Сторонние заряды равномерно распределены
с объемной плотностью ρ>0 по шару
радиусом R
из однородного изотропного диэлектрика
с проницаемостью ε. Найти: а) модуль
вектора напряженности электрического
поля как функцию расстояния r
от центра шара; б) объемную плотность
связанных зарядов.
44.
Сторонние заряды равномерно распределены
с объемной плотностью ρ>0 по шару
радиусом R
из однородного изотропного диэлектрика
с проницаемостью ε. Найти: а) модуль
вектора напряженности электрического
поля как функцию расстояния r
от центра шара; б) объемную плотность
связанных зарядов.













 Дано:
Решение:
Дано:
Решение:
























 4
4
 Дано:
Решение:
Дано:
Решение: a
= 4 см Остроградского- Гаусса:
a
= 4 см Остроградского- Гаусса:
 n
ламп
n
ламп











 I
I








 U0
U
U0
U




 ано:
Решение:
ано:
Решение: 0
= 127 В
0
= 127 В













 ано:
Решение:
ано:
Решение: U
= 1000 В падение напряжения на нём
U
= 1000 В падение напряжения на нём